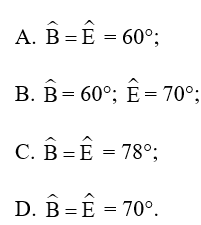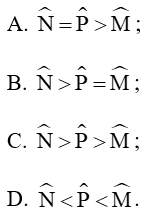30 câu Trắc nghiệm Tam giác bằng nhau (có đáp án 2024) – Toán 7 Chân trời sáng tạo
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 2: Tam giác bằng nhau đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 2.
Trắc nghiệm Toán 7 Bài 2: Tam giác bằng nhau
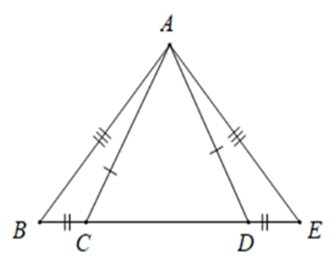
Câu 1: Cho hình vẽ sau. Tam giác nào bằng với tam giác ABC?
A. ∆ABC = ∆EDA;
B. ∆ABC = ∆EAD;
C. ∆ABC = ∆AED;
D. ∆ABC = ∆ADE.
Đáp án đúng là: C
Xét ∆ABC và ∆AED, có:
AB = AE (gt)
BC = DE (gt)
AC = AD (gt)
Nên ∆ABC = ∆AED (c.c.c).
Vậy đáp án C đúng.
Câu 2: Cho hình vẽ sau. Biết PM = PQ, ^MPN=^QPN . Hỏi tam giác nào bằng với tam giác MPN?
A. ∆MPN = ∆QPN;
B. ∆MPN= ∆NPQ;
C. ∆MPN = ∆PNQ;
D. ∆MPN = ∆PQN.
Đáp án đúng là: A
Xét ∆MPN và ∆QPN, có:
PM = PQ (gt)
^MPN=^QPN (gt)
PN là cạnh chung
Nên ∆MPN = ∆QPN (c.g.c).
Vậy đáp án A đúng.
Câu 3: Cho ∆ABC = ∆MNP. Khẳng định nào sau đây là sai?
A. AB = MN;
B. AC = NP;
C. ˆA=ˆM ;
D. ˆP=ˆC ;
Đáp án đúng là: B
Ta có: ∆ABC = ∆MNP Nên ˆA=ˆM ; ˆP=ˆC ; AB = MN; AC = MP; BC = NP
Nên đáp án A, C, D đúng, B sai.
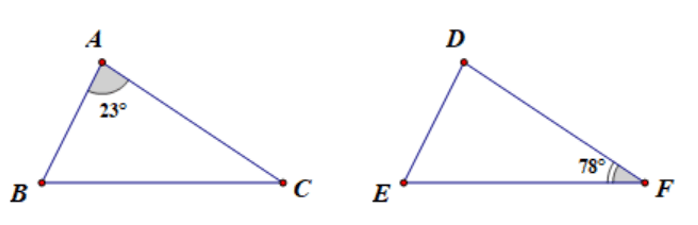
Câu 4: Cho ∆ABC = ∆DEF. Biết ˆA = 23°. Khi đó:
A. ˆD = 23°;
B. ˆD = 32°;
C. ˆE = 23°;
D. ˆE = 32°.
Đáp án đúng là: A
Ta có: ∆ABC = ∆DEF nên ˆD=ˆA (hai góc tương ứng)
Nên ˆD = 23°
Câu 5: Hai tam giác bằng nhau là:
A. Hai tam giác có ba cặp cạnh tương ứng bằng nhau;
B. Hai tam giác có ba cặp góc tương ứng bằng nhau;
C. Hai tam giác có ba cặp cạnh, ba cặp góc tương ứng bằng nhau;
D. Hai tam giác có hai cạnh bằng nhau.
Đáp án đúng là: C
Hai tam giác có ba cặp cạnh, ba cặp góc tương ứng bằng nhau.
Câu 6: Cho ∆ABC = ∆DEF. Biết ˆA = 32°, ˆF = 78°. Tính ˆB;ˆE .
Đáp án đúng là: D
Ta có: ∆ABC = ∆DEF nên ˆD=ˆA=32°, , (các cặp góc tương ứng bằng nhau)
Xét ∆ABC có (định lý tổng ba góc trong tam giác)
Suy ra
= 180 - ( 32 + 78)
= 180 - 110 = 70
Vậy
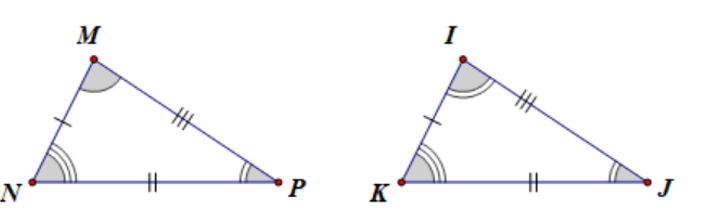
Câu 7: Cho hai tam giác MNP và IKJ có: MN = IK; NP = KJ; MP = JI; ; ; .Khi đó:
A. ∆MNP = ∆IJK;
B. ∆MNP = ∆IKJ;
C. ∆MNP = ∆KIJ;
D. ∆MNP = ∆JKL.
Đáp án đúng là: B
Xét ∆MNP và ∆IKJ có:
MN = IK; NP = KJ; MP = JI; ; ; .
Nên ∆MNP và ∆IKJ.
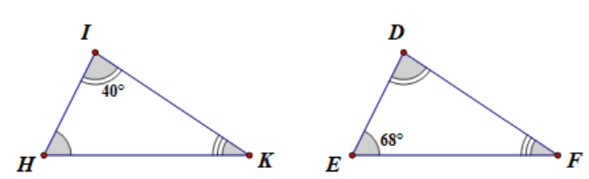
Câu 8: Cho ∆IHK = ∆DEF. Biết = 40°, = 68°. Tính .
Đáp án đúng là: D
Ta có: ∆IHK = ∆DEF nên , (các cặp góc tương ứng bằng nhau)
Xét ∆IHK có (định lý tổng ba góc trong tam giác)
Suy ra:
=
Vậy
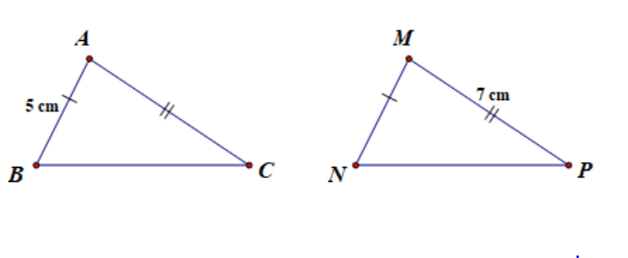
Câu 9: Cho ∆ABC = ∆MNP. Biết AB = 5 cm, MP = 7 cm và chu vi của ∆ABC bằng 22 cm. Tính các cạnh còn lại của mỗi tam giác.
A. NP = BC = 9 cm;
B. NP = BC = 11 cm;
C. NP = BC = 10 cm;
D. NP = 9 cm; BC = 10 cm.
Đáp án đúng là: C
Ta có ∆ABC = ∆MNP nên AB = MN = 5cm, AC = MP = 7cm, BC = NP (các cạnh tương ứng bằng nhau)
Chu vi tam giác ABC là: AB + AC + BC = 22cm
Nên BC = 22 – (AB + AC)
= 22 – (5 + 7) = 22 – 12 = 10 (cm).
Vậy NP = BC = 10 cm.
Câu 10: Cho ∆ABC = ∆MNP. Biết AB = 7 cm, MP = 10 cm và chu vi của tam giác 24 cm. Tính các cạnh còn lại của mỗi tam giác.
A. MN = AC = 7 cm; BC = NP = 10 cm;
B. MN = AC = 10 cm; BC = NP = 7 cm;
C. MN = 7 cm; AC = 10 cm; BC = NP = 7 cm;
D. MN = 10 cm; AC = 7 cm; BC = NP = 7 cm.
Đáp án đúng là: C
Ta có ∆ABC = ∆MNP nên AB = MN = 7cm, AC = MP = 10cm, BC = NP (các cạnh tương ứng bằng nhau)
Chu vi tam giác ABC là: AB + AC + BC = 24 (cm).
Nên BC = 24 – (AB + AC)
= 24 – (7 + 10) = 24 – 17 = 7 (cm).
Suy ra NP = BC = 7 cm.
Vậy MN = 7 cm; AC = 10 cm; BC = NP = 7 cm.
Câu 11: Cho ∆ABC = ∆DEF. Biết rằng AB = 6 cm; AC = 8 cm; EF = 10 cm. Tính chu vi ∆DEF là:
A. 24 cm;
B. 20 cm;
C. 18 cm;
D. 30 cm.
Đáp án đúng là: A
Ta có: ∆ABC = ∆DEF nên AB = DE = 6 cm; AC = DF = 8 cm, BC = EF = 10 cm (các cạnh tương ứng bằng nhau).
Chu vi tam giác DEF là:
DE + DF + EF = 6 + 8 + 10 = 24 (cm).
Vậy chu vi tam giác DEF là 24 cm.
Câu 12: Cho ∆ABC = ∆DEF. Biết rằng AB = 5 cm; AC = 12 cm; EF = 13 cm. Tính chu vi ∆DEF là:
A. 30 cm;
B. 22 cm;
C. 18 cm;
D. 20 cm.
Đáp án đúng là: A
Ta có: ∆ABC = ∆DEF nên AB = DE = 5 cm; AC = DF = 12 cm, BC = EF = 13 cm (các cạnh tương ứng bằng nhau).
Chu vi tam giác DEF là:
DE + DF + EF = 5 + 12 + 13 = 30 (cm).
Câu 13: Cho ∆ABC = ∆DEF. Biết ; . Tính .
Đáp án đúng là: C
Ta có ∆ABC = ∆DEF nên: =
Xét tam giác ABC có:
(gt)
Suy ra
Lại có
Suy ra =
Vậy ;
Câu 14: Cho ∆ABC = ∆MNP, trong đó . So sánh các góc A; B; C.
Đáp án đúng là: C
Ta có ∆ABC = ∆MNP nên (hai góc tương ứng)
Xét tam giác ABC có
Nên
Vì
Câu 15: Cho ∆ABC = ∆MNP, trong đó . So sánh các góc N; M; P.
Đáp án đúng là: C
Vì ∆ABC = ∆MNP nên: = 30°; = 60°; .
Xét tam giác MNP có: = 180°.
Nên = 180° − − = 180° – 30° – 60° = 90°
Vậy .