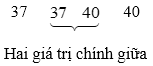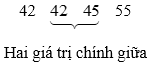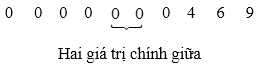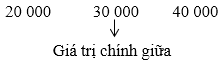Lý thuyết Các số đặc trưng của mẫu số liệu không ghép nhóm (Kết nối tri thức 2024) Toán 10

Lý thuyết Toán lớp 10 Chương 5: Các số đặc trưng của mẫu số liệu không ghép nhóm

A. Lý thuyết Chương 5: Các số đặc trưng của mẫu số liệu không ghép nhóm

1. Số gần đúng

Trong nhiều trường hợp, ta không biết hoặc khó biết số đúng (kí hiệu là $\overline{a}$) mà chỉ tìm được giá trị xấp xỉ nó. Giá trị này được gọi là số gần đúng, kí hiệu là a.

Chú ý:

Ta có thể sử dụng máy tính cầm tay để tìm giá trị gần đúng của các biểu thức chứa các số vô tỉ như π, $\sqrt{a},\sqrt[3]{a}$,...

2. Sai số tuyệt đối và sai số tương đối

a) Sai số tuyệt đối

Giá trị ${\Delta }_a=\left(a-\overline{a}\right)$phản ánh mức độ sai lệch giữa số đúng $\overline{a}$và số gần đúng a, được gọi là sai số tuyệt đối của số gần đúng a.

Ví dụ:

Ta có: $3^7.\sqrt{6}\approx 5357$.

Suy ra $\overline{a}=3^7.\sqrt{6}$là số đúng; a = 5357 là số gần đúng.

Khi đó ta có: ${\Delta }_a=\left(a-\overline{a}\right)=\left(5357-3^7.\sqrt{6}\right)\approx \mathrm{0,034}$.

Vậy ∆a = 0,034 là sai số tuyệt đối của số gần đúng a = 5357.

Chú ý:

+ Trên thực tế, nhiều khi ta không biết $\overline{a}$nên cũng không biết ∆a. Tuy nhiên, ta có thể đánh giá được ∆a không vượt quá một số dương d nào đó.

+ Nếu ∆a ≤ d thì a – d ≤ $\overline{a}$≤ a + d, khi đó ta viết $\overline{a}$= a ± d và hiểu là số đúng $\overline{a}$nằm trong đoạn [a – d; a + d]. Do đó d càng nhỏ thì a càng gần $\overline{a}$nên d được gọi là độ chính xác của số gần đúng.

+ Trong các phép đo, độ chính xác d của số gần đúng bằng một nửa đơn vị của thước đo. Chẳng hạn, một thước đo có chia vạch đến xentimét thì mọi giá trị đo nằm giữa 6,5cm và 7,5cm đều được coi là 7cm. Vì vậy, thước đo có thang đo càng nhỏ thì cho giá trị đo càng chính xác.

b) Sai số tương đối

Sai số tương đối của số gần đúng a, kí hiệu là δa, là tỉ số giữa sai số tuyệt đối và |a|, tức là ${\delta }_a=\frac{{\Delta }_a}{\left(a\right)}$.

Ví dụ: Bao bì của một chai nước suối có ghi thể tích thực là 350ml, biết rằng sai số tuyệt đối là 2ml. Tìm sai số tương đối của chai nước suối.

Hướng dẫn giải

Ta có a = 350 (ml) và ∆a = 2 (ml), do đó sai số tương đối là:

${\delta }_a=\frac{{\Delta }_a}{\left(a\right)}=\frac{2}{350}\approx \mathrm{0,57}\%$.

Nhận xét:

Nếu $\overline{a}=a\pm d$thì ∆a ≤ d, do đó ${\delta }_a\le \frac{d}{\left(a\right)}$. Nếu $\frac{d}{\left(a\right)}$càng nhỏ thì chất lượng của phép đo hay tính toán càng cao. Người ta thường viết sai số tương đối dưới dạng phần trăm.

3. Quy tròn số gần đúng

Số thu được sau khi thực hiện làm tròn số được gọi là số quy tròn. Số quy tròn là một số gần đúng của số ban đầu.

Chú ý:

•Đối với chữ số hàng làm tròn:

+ Giữ nguyên nếu chữ số ngay bên phải nó nhỏ hơn 5;

+ Tăng 1 đơn vị nếu chữ số ngay bên phải nó lớn hơn hoặc bằng 5.

•Đối với chữ số sau hàng làm tròn:

+ Bỏ đi nếu ở phần thập phân;

+ Thay bởi các chữ số 0 nếu ở phần số nguyên.

Nhận xét:

+ Khi thay số đúng bởi số quy tròn đến một hàng nào đó thì sai số tuyệt đối của số quy tròn không vượt quá nửa đơn vị của hàng làm tròn.

+ Cho số gần đúng a với độ chính xác d. Khi được yêu cầu làm tròn số a mà không nói rõ làm tròn đến hàng nào thì ta làm tròn số a đến hàng thấp nhất mà d nhỏ hơn 1 đơn vị của hàng đó.

4. Số trung bình và trung vị

a) Số trung bình

Số trung bình (số trung bình cộng) của mẫu số liệu x1, x2,..., xn, kí hiệu là $\overline{x}$được tính bằng công thức:

$\overline{x}=\frac{x_1+x_2+\mathrm{...}+x_n}{n}$

Chú ý:

Trong trường hợp mẫu số liệu cho dưới dạng bảng tần số thì số trung bình được tính theo công thức:

$\overline{x}=\frac{m_1{x}_1+m_2{x}_2+\mathrm{...}+m_k{x}_k}{n}$

trong đó mk là tần số của giá trị xk và n = m1 + m2 +...+ mk.

Ý nghĩa: Số trung bình là giá trị trung bình cộng của các số trong mẫu số liệu, nó cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu.

b) Trung vị

Trong trường hợp mẫu số liệu có giá trị bất thường (rất lớn hoặc rất bé so với đa số các giá trị khác), người ta không dùng số trung bình để đo xu thế trung tâm mà dùng trung vị.

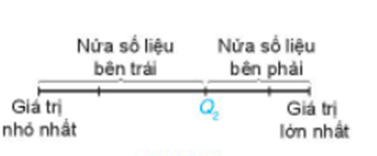
Để tìm trung vị (kí hiệu là Me) của một mẫu số liệu, ta thực hiện như sau:

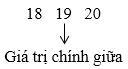
+ Sắp xếp các giá trị trong mẫu số liệu theo thứ tự không giảm.

+ Nếu số giá trị của mẫu số liệu là số lẻ thì giá trị chính giữa của mẫu là trung vị. Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu.

Ý nghĩa: Trung vị không bị ảnh hưởng bởi giá trị bất thường trong khi số trung bình bị ảnh hưởng bởi giá trị bất thường. Vì vậy, khi mẫu số liệu có giá trị bất thường, người ta thường dùng trung vị đại diện cho các số liệu thống kê.

5. Tứ phân vị

Tứ phân vị dùng để xác định ngưỡng để phân loại các số liệu có trong mẫu số liệu.

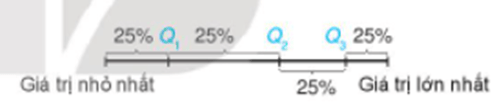
Để tìm các tứ phân vị của mẫu số liệu có n giá trị, ta làm như sau:

+ Sắp xếp mẫu số liệu theo thứ tự không giảm.

+ Tìm trung vị. Giá trị này là Q2.

+ Tìm trung vị của nửa số liệu bên trái Q2 (không bao gồm Q2 nếu n lẻ). Giá trị này là Q1.

+ Tìm trung vị của nửa số liệu bên phải Q2 (không bao gồm Q2 nếu n lẻ). Giá trị này là Q3.

Q1, Q2, Q3 được gọi là các tứ phân vị của mẫu số liệu.

Chú ý: Q1 được gọi là tứ phân vị thứ nhất hay tứ phân vị dưới, Q3 được gọi là tứ phân vị thứ ba hay tứ phân vị trên.

Ý nghĩa: Các điểm Q1, Q2, Q3 chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần đều chứa 25% giá trị.

6. Mốt

Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất.

Ý nghĩa: Có thể dùng mốt để đo xu thế trung tâm của mẫu số liệu khi mẫu số liệu có nhiều giá trị trùng nhau.

Nhận xét:

+ Mốt có thể không là duy nhất. Chẳng hạn, với mẫu số liệu sau:

6959975595

Ta thấy các số 5; 9 đều xuất hiện với số lần lớn nhất (4 lần) nên mẫu số liệu này có hai mốt là 5 và 9.

+ Khi các giá trị trong mẫu số liệu xuất hiện với tần số như nhau thì mẫu số liệu không có mốt. Chẳng hạn, với mẫu số liệu sau:

686786778

Ta thấy các giá trị 6; 7; 8 trong mẫu số liệu đều xuất hiện với tần số như nhau (3 lần) nên mẫu số liệu này không có mốt.

+ Mốt còn được định nghĩa cho mẫu dữ liệu định tính (dữ liệu không phải là số). Ví dụ trong buổi biểu quyết chọn một trong ba bạn Hoa, Bình, Tú làm bí thư của lớp 10C, bạn thư ký của lớp đã tổng kết được kết quả biểu quyết như sau:

Tên bạn được chọn	Hoa	Bình	Tú
Số phiếu	18	12	10

Trong mẫu dữ liệu này, số phiếu chọn “bạn Hoa” nhiều nhất, được gọi là mốt.

7. Khoảng biến thiên và khoảng tứ phân vị

a) Khoảng biến thiên

Khoảng biến thiên, kí hiệu là R, là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu.

Ý nghĩa: Khoảng biến thiên dùng để đo độ phân tán của mẫu số liệu. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.

Nhận xét: Sử dụng khoảng biến thiên có ưu điểm là đơn giản, dễ tính toán song khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất mà bỏ qua thông tin từ tất cả các giá trị khác. Do đó, khoảng biến thiên rất dễ bị ảnh hưởng bởi các giá trị bất thường.

b) Khoảng tứ phân vị

Khoảng tứ phân vị, kí hiệu là ∆Q, là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, tức là:

∆Q = Q3 – Q1.

Về bản chất, khoảng tứ phân vị là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp.

Ý nghĩa: Khoảng tứ phân vị cũng là một số đo độ phân tán của mẫu số liệu. Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán.

Chú ý: Một số tài liệu gọi khoảng biến thiên là biên độ và khoảng tứ phân vị là độ trải giữa.

8. Phương sai và độ lệch chuẩn

Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu (bỏ qua thông tin của tất cả các giá trị khác). Khoảng tứ phân vị chỉ sử dụng thông tin của 50% số liệu chính giữa. Có một vài số đặc trưng khác đo độ phân tán sử dụng thông tin của tất cả các giá trị trong mẫu số liệu. Hai trong số đó là phương sai và độ lệch chuẩn.

Cụ thể với mẫu số liệu x1, x2,..., xn, nếu gọi số trung bình là $\overline{x}$ thì với mỗi giá trị xi, độ lệch của nó so với giá trị trung bình là xi – $\overline{x}$.

•Phương sai là giá trị $s^2=\frac{{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+{\left(x_n-\overline{x}\right)}^2}{n}$.

•Căn bậc hai của phương sai, s = $\sqrt{s^2}$, được gọi là độ lệch chuẩn.

Chú ý: Người ta còn sử dụng đại lượng để đo độ phân tán của mẫu số liệu:

${\hat{s}}^2=\frac{{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+{\left(x_n-\overline{x}\right)}^2}{n-1}$.

Ý nghĩa: Nếu số liệu càng phân tán thì phương sai và độ lệch chuẩn càng lớn.

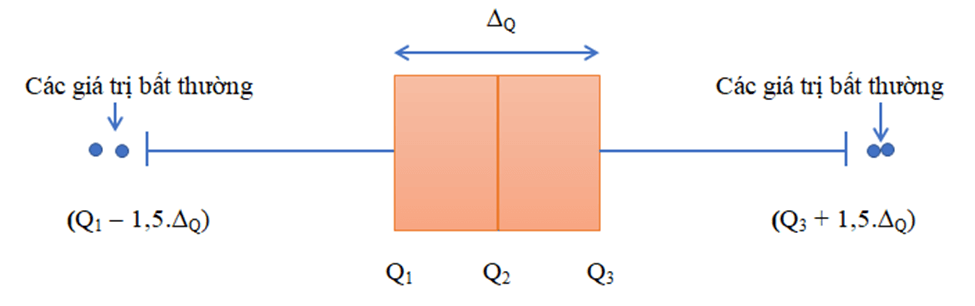
9. Phát hiện số liệu bất thường hoặc không chính xác bằng biểu đồ hộp

Trong mẫu số liệu thống kê, có khi ta sẽ gặp phải những giá trị quá lớn hoặc quá nhỏ so với đa số các giá trị khác. Những giá trị này được gọi là giá trị bất thường. Chúng xuất hiện trong mẫu số liệu có thể do nhầm lẫn hay sai sót nào đó. Ta có thể dùng biểu đồ hộp để phát hiện những giá trị bất thường này.

Các giá trị lớn hơn Q3 + 1,5 . ∆Q hoặc bé hơn Q1 – 1,5 . ∆Q được xem là giá trị bất thường.

B. Bài tập tự luyện

Bài 1. Làm tròn số 4372,8 đến hàng chục và 8,125 đến hàng phần trăm rồi tính sai số tuyệt đối của số quy tròn.

Hướng dẫn giải

+ Số quy tròn của số 4372,8 đến hàng chục là 4370. Sai số tuyệt đối là

∆ = |4370 − 4372,8| = 2,8.

+ Số quy tròn của số 8,125 đến hàng phần trăm là 8,13. Sai số tuyệt đối là

∆' = |8,13 – 8,125| = 0,005.

Bài 2. Giải thích kết quả “Đo độ sâu của mực nước biển ở một vùng cho kết quả là 2136 ± 5 m” và thực hiện làm tròn số gần đúng.

Hướng dẫn giải

Độ sâu thực tế của mực nước biển $\overline{a}$là số đúng. Tuy không biết $\overline{a}$nhưng ta biết kết quả đo đạc là 2136 m nên 2136 là số gần đúng cho $\overline{a}$. Độ chính xác d = 5 (m).

Vì độ chính xác đến hàng đơn vị (d = 5) nên ta làm tròn đến hàng chục theo quy tắc làm tròn. Do đó số quy tròn của a là 2140.

Bài 3. Các nhà vật lý sử dụng ba phương pháp đo hằng số Hubble lần lượt cho kết quả như sau:

67,31 ± 0,96;

67,90 ± 0,55;

67,74 ± 0,46.

Phương pháp nào chính xác nhất tính theo sai số tương đối?

Hướng dẫn giải

Với phương pháp đo thứ nhất: a1 = 67,31 và d1 = 0,96, do đó sai số tương đối là:

${\delta }_1\le \frac{d_1}{\left(a_1\right)}=\frac{\mathrm{0,96}}{\mathrm{67,31}}\approx \mathrm{1,4}\%$

Với phương pháp đo thứ hai: a2 = 67,90 và d2 = 0,55, do đó sai số tương đối là:

${\delta }_2\le \frac{d_2}{\left(a_2\right)}=\frac{\mathrm{0,55}}{\mathrm{67,90}}\approx \mathrm{0,81}\%$

Với phương pháp đo thứ ba: a3 = 67,74 và d3 = 0,46, do đó sai số tương đối là:

${\delta }_3\le \frac{d_3}{\left(a_3\right)}=\frac{\mathrm{0,46}}{\mathrm{67,74}}\approx \mathrm{0,68}\%$

Vì 0,68% < 0,81% < 1,4% nên δ3 < δ2 < δ1.

Do đó phương pháp đo thứ ba là chính xác nhất tính theo sai số tương đối.

Bài 4. Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:

a) Tuổi thọ (tính theo năm) của 6 loại bóng đèn được ghi lại như sau:

19 20 31 18 26 24

b) Số cân nặng (tính theo kg) của 9 học sinh lớp 10D được ghi lại như sau:

373740424540424255

Hướng dẫn giải

a) Tuổi thọ trung bình của 6 loại bóng đèn là:

$\frac{19+20+31+18+26+24}{6}$= 23 (năm)

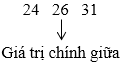
+ Ta tìm trung vị của mẫu số liệu:

Sắp xếp các giá trị đã cho theo thứ tự không giảm:

Dãy trên có hai giá trị chính giữa lần lượt là 20 và 24.

Vậy trung vị của mẫu số liệu là: $\frac{20+24}{2}=22$.

+ Vì các giá trị 18; 19; 20; 24; 26; 31 trong mẫu số liệu đều xuất hiện với tần số như nhau (1 lần) nên mẫu số liệu này không có mốt.

+ Ta tìm tứ phân vị của mẫu số liệu:

Giá trị Q2 chính là trung vị của mẫu số liệu. Do đó ta có Q2 = 22.

Ta tìm Q1 là trung vị của nửa số liệu bên trái Q2:

Giá trị chính giữa lúc này là 19. Ta suy ra Q1 = 19.

Ta tìm Q3 là trung vị của nửa số liệu bên phải Q2:

Giá trị chính giữa lúc này là 26. Ta suy ra Q3 = 26.

Vậy các tứ phân vị của mẫu số liệu là Q1 = 19; Q2 = 22; Q3 = 26.

b) Số cân nặng trung bình của 9 học sinh lớp 10D là:

$\frac{37.2+40.2+42.3+45+55}{6}\approx \mathrm{63,33}\left(kg\right)$

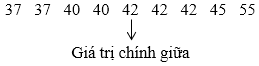
+ Ta tìm trung vị của mẫu số liệu:

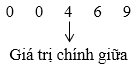
Sắp xếp các giá trị đã cho theo thứ tự không giảm:

Trung vị của mẫu số liệu là: 42.

+ Ta thấy giá trị 42 xuất hiện với tần số cao nhất (3 lần) nên mốt của mẫu số liệu này là 42.

+ Ta tìm tứ phân vị của mẫu số liệu:

Giá trị Q2 chính là trung vị của mẫu số liệu. Do đó ta có Q2 = 42.

Ta tìm Q1 là trung vị của nửa số liệu bên trái Q2:

Dãy trên có hai giá trị chính giữa là 37 và 40. Do đó Q1 = (37 + 40) : 2 = 38,5.

Ta tìm Q3 là trung vị của nửa số liệu bên phải Q2:

Dãy trên có hai giá trị chính giữa là 42 và 45. Do đó Q3 = (42 + 45) : 2 = 43,5.

Vậy các tứ phân vị của mẫu số liệu là Q1 = 38,5; Q2 = 42; Q3 = 43,5.

Bài 5. Số lượng học sinh giỏi Quốc gia năm học 2019 – 2020 của 10 trường Trung học phổ thông được cho như sau:

0 0 9 0 0 4 0 0 0 6

a) Tìm số trung bình, mốt và các tứ phân vị của mẫu số liệu trên.

b) Giải thích tại sao tứ phân vị thứ nhất và trung vị trùng nhau.

Hướng dẫn giải

a) Số lượng học sinh trung bình là: $\frac{0.7+9+4+6}{10}$= 1,9 (học sinh)

+ Ta tìm trung vị của mẫu số liệu:

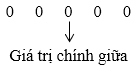
Sắp xếp các giá trị đã cho theo thứ tự không giảm:

Dãy trên có hai giá trị chính giữa cùng bằng 0.

Vậy trung vị của mẫu số liệu cũng bằng 0.

+ Ta thấy giá trị 0 xuất hiện với tần số cao nhất (7 lần) nên mốt của mẫu số liệu này là 0.

+ Ta tìm tứ phân vị của mẫu số liệu:

Giá trị Q2 chính là trung vị của mẫu số liệu. Do đó ta có Q2 = 0.

Ta tìm Q1 là trung vị của nửa số liệu bên trái Q2:

Giá trị chính giữa lúc này là 0. Ta suy ra Q1 = 0.

Ta tìm Q3 là trung vị của nửa số liệu bên phải Q2:

Giá trị chính giữa lúc này là 4. Ta suy ra Q3 = 4.

Vậy các tứ phân vị của mẫu số liệu là Q1 = 0; Q2 = 0; Q3 = 4.

b) Vì mẫu số liệu tập trung với mật độ cao ở bên trái Q2, tức là trung vị, nên tứ phân vị thứ nhất Q1 và trung vị Q2 trùng nhau.

Bài 6. Sức chứa của một số sân vận động tại Việt Nam đã được thống kê và ghi lại như trong bảng sau (số liệu gần đúng):

Các giá trị số trung bình, trung vị và mốt bị ảnh hưởng như thế nào nếu bỏ đi số liệu sức chứa của sân vận động Cần Thơ?

Hướng dẫn giải

+ Trước khi bỏ đi số liệu sức chứa của sân vận động Cần Thơ, ta có:

Sức chỗ ngồi trung bình là:

$\frac{40000+50000+30000+20000}{4}$ = 35 000.

Sắp xếp các giá trị đã cho theo thứ tự không giảm:

Dãy trên có hai giá trị chính giữa lần lượt là 30 000 và 40 000.

Do đó trung vị của mẫu số liệu là: $\frac{30000+40000}{2}$ = 35 000.

Trong mẫu dữ liệu trên, sức chứa ở sân vận động Cần Thơ là lớn nhất.

Do đó mốt của mẫu dữ liệu trên là “Cần Thơ”.

+ Sau khi bỏ đi số liệu sức chứa của sân vận động Cần Thơ, ta có:

Sức chỗ ngồi trung bình là:

$\frac{40000+30000+20000}{3}$ = 30 000.

Sắp xếp các giá trị đã cho theo thứ tự không giảm:

Dãy trên có giá trị chính giữa lần lượt là 30 000.

Do đó trung vị của mẫu số liệu là: 30 000.

Trong mẫu dữ liệu trên, sức chứa ở sân vận động Mỹ Đình là lớn nhất.

Do đó mốt của mẫu dữ liệu trên là “Mỹ Đình”.

+ Nếu bỏ đi số liệu sức chứa của sân vận động Cần Thơ, ta thấy:

Giá trị số trung bình và trung vị đều giảm 5000 (giảm từ 35 000 xuống còn 30 000).

Mốt của dữ liệu cũng bị thay đổi từ “Cần Thơ” sang “Mỹ Đình”.

Bài 7. Mỗi khẳng định sau đúng hay sai?

a) Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch chuẩn càng lớn;

b) Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất, bỏ qua thông tin của các giá trị còn lại;

c) Khoảng tứ phân vị có sử dụng thông tin của các giá trị lớn nhất và giá trị bé nhất;

d) Các số đo độ phân tán đều không âm.

Hướng dẫn giải

a) Sai.

Nếu các giá trị của mẫu số liệu đều tập trung quanh giá trị trung bình thì độ lệch của mỗi giá trị xi – $\overline{x}$càng nhỏ.

Ta suy ra (x­i­ – $\overline{x}$)2 cũng càng nhỏ.

Do đó tổng các bình phương độ lệch cũng càng nhỏ.

Mà độ lệch chuẩn tỉ lệ thuận với tổng các bình phương độ lệch.

Vậy trong trường hợp này, độ lệch chuẩn càng nhỏ.

b) Đúng.

Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất mà bỏ qua thông tin từ tất cả các giá trị khác. Do đó, khoảng biến thiên rất dễ bị ảnh hưởng bởi các giá trị bất thường.

c) Sai.

Khoảng tứ phân vị chỉ sử dụng 50% số liệu chính giữa của mẫu số liệu đã sắp xếp.Vậy khoảng biến thiên không sử dụng giá trị lớn nhất và giá trị bé nhất.

d) Đúng.

Khoảng biến thiên là hiệu của giá trị lớn nhất và giá trị bé nhất. Do đó khoảng biến thiên luôn không âm.

Khoảng tứ phân vị là hiệu của tứ phân vị thứ ba và tứ phân vị thứ nhất. Do đó khoảng tứ phân vị luôn không âm.

Phương sai là tổng các bình phương các độ lệch nên luôn không âm.

Độ lệch chuẩn là căn bậc hai của phương sai nên độ lệch chuẩn luôn không âm.

Bài 8. Mẫu số liệu sau đây cho biết cân nặng của 10 trẻ sơ sinh (đơn vị kg):

2,8 2,5 3,1 3,3 2,9 3,5 4,1 2,8 3,0 3,3

Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn cho mẫu số liệu trên.

Hướng dẫn giải

+ Khoảng biến thiên:

Số cân nặng cao nhất, thấp nhất lần lượt là 4,1 (kg) và 2,5 (kg). Do đó khoảng biến thiên là R = 4,1 – 2,5 = 1,6 (kg).

+ Khoảng tứ phân vị:

Trước hết, ta sắp xếp mẫu số liệu theo thứ tự không giảm:

2,52,82,82,93,03,13,33,33,54,1

Mẫu số liệu trên gồm 10 giá trị, hai phần tử chính giữa là 3,0 và 3,1.

Do đó trung vị là Q2 = (3,0 + 3,1) : 2 = 3,05.

Nửa số liệu bên trái là 2,5; 2,8; 2,8; 2,9; 3,0 gồm 5 giá trị. Do đó trung vị là số ở vị trí chính giữa Q1 = 2,8.

Nửa số liệu bên phải là 3,1; 3,3; 3,3; 3,5; 4,1 gồm 5 giá trị, Do đó trung vị là số ở vị trí chính giữa Q3 = 3,3.

Vậy khoảng tứ phân vị cho mẫu số liệu là ∆Q = Q3 – Q1 = 3,3 – 2,8 = 0,5.

+ Độ lệch chuẩn:

Số trung bình của mẫu số liệu là:

$\overline{x}=\frac{\mathrm{2,5}+\mathrm{2,8.2}+\mathrm{2,9}+\mathrm{3,0}+\mathrm{3,1}+\mathrm{3,3.2}+\mathrm{3,5}+\mathrm{4,1}}{10}$= 3,13

Ta có bảng sau:

Giá trị	Độ lệch	Bình phương độ lệch
2,8	2,8 – 3,13 = – 0,33	0,1089
2,5	2,5 – 3,13 = – 0,63	0,3969
3,1	3,1 – 3,13 = – 0,03	0,0009
3,3	3,3 – 3,13 = 0,17	0,0289
2,9	2,9 – 3,13 = – 0,23	0,0529
3,5	3,5 – 3,13 = 0,37	0,1369
4,1	4,1 – 3,13 = 0,97	0,9409
2,8	2,8 – 3,13 = – 0,33	0,1089
3,0	3,0 – 3,13 = – 0,13	0,0169
3,3	3,3 – 3,13 = 0,17	0,0289
Tổng		1,821

Mẫu số liệu gồm 10 giá trị nên n = 10. Do đó phương sai là: s2 = $\frac{\mathrm{1,821}}{10}$= 0,1821.

Độ lệch chuẩn là: s = $\sqrt{\mathrm{0,1821}}$≈ 0,4267.

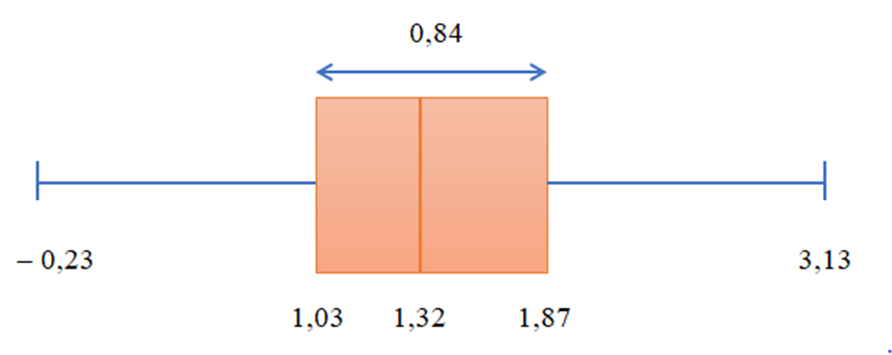
Bài 9. Tỉ lệ thất nghiệp từ năm 2006 – 2020 tại Việt Nam (đơn vị %) được cho như sau:

0,00; 2,03; 0,00; 1,74; 1,11; 1,00; 1,03; 1,32; 1,26; 1,85; 1,85; 1,87; 1,16; 2,04; 2,39.

Hãy tìm các giá trị bất thường (nếu có) của mẫu số liệu trên.

Hướng dẫn giải

Sắp xếp các số liệu theo thứ tự không giảm ta có:

0,00; 0,00; 1,00; 1,03; 1,11; 1,16; 1,26; 1,32; 1,74; 1,85; 1,85; 1,87; 2,03; 2,04; 2,39.

Từ mẫu số liệu trên, ta tính được Q2 = 1,32; Q1 = 1,03 và Q3 = 1,87. Do đó khoảng tứ phân vị là:

∆Q = Q3 – Q1 = 1,87 – 1,03 = 0,84.

Biểu đồ hộp cho mẫu số liệu này là:

Ta có Q1 – 1,5.∆Q = – 0,23 và Q3 + 1,5.∆Q = 3,13 nên trong mẫu số liệu trên không có giá trị nào được xem là bất thường.