Lý thuyết Các số đặc trưng đo độ phân tán (Kết nối tri thức 2024) Toán 10

Lý thuyết Toán lớp 10 Bài 14: Các số đặc trưng đo độ phân tán

A.Lý thuyết Các số đặc trưng đo độ phân tán

1. Khoảng biến thiên và khoảng tứ phân vị

a) Khoảng biến thiên

Khoảng biến thiên, kí hiệu là R, là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu.

Ý nghĩa: Khoảng biến thiên dùng để đo độ phân tán của mẫu số liệu. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.

Ví dụ: Hai xạ thủ A và B cùng bắn 10 phát đạn, kết quả được ghi lại như bảng sau:

a) Điểm số trung bình của hai xạ thủ A và B có như nhau không?

b) Tính các khoảng biến thiên của hai mẫu số liệu. Căn cứ trên chỉ số này, xạ thủ nào bắn đều hơn?

Hướng dẫn giải

a) Điểm số trung bình của xạ thủ A là: $\frac{7.2+8.2+9.4+10.2}{10}$= 8,6 (điểm).

Điểm số trung bình của xạ thủ B là: $\frac{6+7.2+8+9.2+10.4}{10}$= 8,6 (điểm)

Vậy điểm kiểm tra trung bình của hai xạ thủ A và B đều bằng 8,6.

b) Đối với xạ thủ A: Điểm số thấp nhất và cao nhất tương ứng là 7 và 10. Do đó khoảng biến thiên là RA = 10 – 7 = 3.

Đối với xạ thủ B: Điểm số thấp nhất và cao nhất tương ứng là 6 và 10. Do đó khoảng biến thiên là RB = 10 – 6 = 4.

Do RB > RA nên ta nói xạ thủ A bắn đều hơn xạ thủ B.

Nhận xét: Sử dụng khoảng biến thiên có ưu điểm là đơn giản, dễ tính toán song khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất mà bỏ qua thông tin từ tất cả các giá trị khác. Do đó, khoảng biến thiên rất dễ bị ảnh hưởng bởi các giá trị bất thường.

b) Khoảng tứ phân vị

Khoảng tứ phân vị, kí hiệu là ∆Q, là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, tức là:

∆Q = Q3 – Q1.

Về bản chất, khoảng tứ phân vị là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp.

Ý nghĩa: Khoảng tứ phân vị cũng là một số đo độ phân tán của mẫu số liệu. Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán.

Chú ý: Một số tài liệu gọi khoảng biến thiên là biên độ và khoảng tứ phân vị là độ trải giữa.

Ví dụ: Mẫu số liệu sau cho biết số ghế trống tại một rạp xiếc trong 9 ngày:

0739201151619

Tìm khoảng tứ phân vị cho mẫu số liệu trên.

Hướng dẫn giải

Trước hết, ta sắp xếp mẫu số liệu theo thứ tự không giảm:

0357911161920

Mẫu số liệu trên gồm 9 giá trị nên trung vị là số ở vị trí chính giữa Q2 = 9.

Nửa số liệu bên trái là 0; 3; 5; 7 gồm 4 giá trị, hai phần tử chính giữa là 3; 5.

Do đó, Q1 = (3 + 5) : 2 = 4.

Nửa số liệu bên phải là 11; 16; 19; 20 gồm 4 giá trị, hai phần tử chính giữa là 16; 19.

Do đó, Q3 = (16 + 19) : 2 = 17,5.

Vậy khoảng tứ phân vị cho mẫu số liệu là ∆Q = Q3 – Q1 = 17,5 – 4 = 13,5.

2. Phương sai và độ lệch chuẩn

Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu (bỏ qua thông tin của tất cả các giá trị khác). Khoảng tứ phân vị chỉ sử dụng thông tin của 50% số liệu chính giữa. Có một vài số đặc trưng khác đo độ phân tán sử dụng thông tin của tất cả các giá trị trong mẫu số liệu. Hai trong số đó là phương sai và độ lệch chuẩn.

Cụ thể với mẫu số liệu x1, x2,..., xn, nếu gọi số trung bình là $\overline{x}$ thì với mỗi giá trị xi, độ lệch của nó so với giá trị trung bình là xi – $\overline{x}$.

•Phương sai là giá trị $s^2=\frac{{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+{\left(x_n-\overline{x}\right)}^2}{n}$.

•Căn bậc hai của phương sai, s = $\sqrt{s^2}$, được gọi là độ lệch chuẩn.

Chú ý: Người ta còn sử dụng đại lượng để đo độ phân tán của mẫu số liệu:

${\hat{s}}^2=\frac{{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+{\left(x_n-\overline{x}\right)}^2}{n-1}$.

Ý nghĩa: Nếu số liệu càng phân tán thì phương sai và độ lệch chuẩn càng lớn.

Ví dụ: Mẫu số liệu sau đây cho biết số học sinh được lên lớp của 7 lớp khối 10 tại một trường Trung học phổ thông:

45424740414442

Tìm phương sai và độ lệch chuẩn cho mẫu số liệu trên. Qua các đại lượng này, em có nhận xét gì về độ phân tán của mẫu số liệu?

Hướng dẫn giải

Số trung bình của mẫu số liệu là: $\overline{x}=\frac{45+42+47+40+41+44+42}{7}$= 43.

Ta có bảng sau:

Mẫu số liệu gồm 7 giá trị nên n = 7. Do đó phương sai là: s2 = $\frac{36}{7}$≈ 5,14.

Độ lệch chuẩn là: s = $\sqrt{\mathrm{5,14}}$≈ 2,27.

Qua các đại lượng này, ta thấy phương sai và độ lệch chuẩn không lớn nên số liệu không quá phân tán.

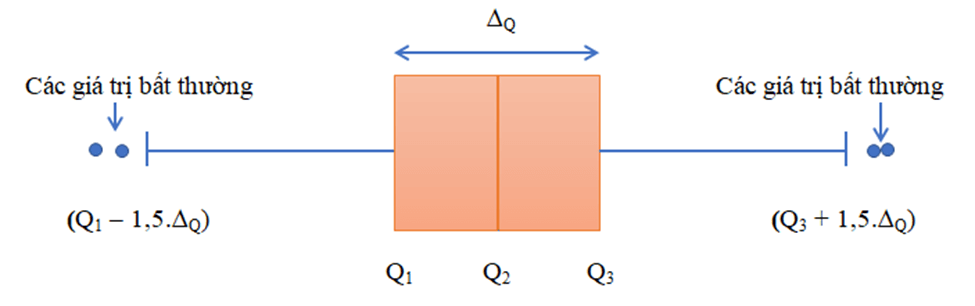
3. Phát hiện số liệu bất thường hoặc không chính xác bằng biểu đồ hộp

Trong mẫu số liệu thống kê, có khi ta sẽ gặp phải những giá trị quá lớn hoặc quá nhỏ so với đa số các giá trị khác. Những giá trị này được gọi là giá trị bất thường. Chúng xuất hiện trong mẫu số liệu có thể do nhầm lẫn hay sai sót nào đó. Ta có thể dùng biểu đồ hộp để phát hiện những giá trị bất thường này.

Các giá trị lớn hơn Q3 + 1,5. ∆Q hoặc bé hơn Q1 –1,5. ∆Q được xem là giá trị bất thường.

Ví dụ: Hàm lượng Canxi (đơn vị mg) trong 100 g một số loại thực phẩm được cho như trong bảng sau:

Tìm giá trị bất thường trong mẫu số liệu trên bằng cách sử dụng biểu đồ hộp.

Hướng dẫn giải

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

0; 4; 8; 10; 13; 14; 15; 16; 16; 18; 18; 18; 19; 20; 20; 20; 21; 22; 29; 34.

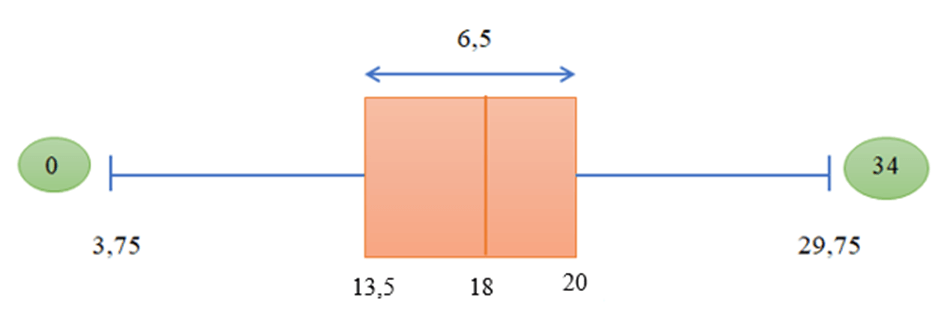
Từ mẫu số liệu trên, ta tính được Q2 = 18; Q1 = 13,5 và Q3 = 20. Do đó khoảng tứ phân vị là:

∆Q = Q3 – Q1 = 20 – 13,5 = 6,5.

Biểu đồ hộp cho mẫu số liệu này là:

Ta có Q1 – 1,5.∆Q = 3,75 và Q3 + 1,5.∆Q = 29,75 nên trong mẫu số liệu có hai giá trị được xem là bất thường là 0 mg (bé hơn 3,75 mg) và 34 mg (lớn hơn 29,75 mg).

B. Bài tập tự luyện

Bài 1. Mẫu số liệu sau đây cho biết cân nặng của 10 trẻ sơ sinh (đơn vị kg):

2,8 2,5 3,1 3,3 2,9 3,5 4,1 2,8 3,0 3,3

Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn cho mẫu số liệu trên.

Hướng dẫn giải

+ Khoảng biến thiên:

Số cân nặng cao nhất, thấp nhất lần lượt là 4,1 (kg) và 2,5 (kg). Do đó khoảng biến thiên là R = 4,1 – 2,5 = 1,6 (kg).

+ Khoảng tứ phân vị:

Trước hết, ta sắp xếp mẫu số liệu theo thứ tự không giảm:

2,52,82,82,93,0 3,13,33,33,54,1

Mẫu số liệu trên gồm 10 giá trị, hai phần tử chính giữa là 3,0 và 3,1.

Do đó trung vị là Q2 = (3,0 + 3,1) : 2 = 3,05.

Nửa số liệu bên trái là 2,5; 2,8; 2,8; 2,9; 3,0 gồm 5 giá trị. Do đó trung vị là số ở vị trí chính giữa Q1 = 2,8.

Nửa số liệu bên phải là 3,1; 3,3; 3,3; 3,5; 4,1 gồm 5 giá trị, Do đó trung vị là số ở vị trí chính giữa Q3 = 3,3.

Vậy khoảng tứ phân vị cho mẫu số liệu là ∆Q = Q3 – Q1 = 3,3 – 2,8 = 0,5.

+ Độ lệch chuẩn:

Số trung bình của mẫu số liệu là:

$\overline{x}=\frac{\mathrm{2,5}+\mathrm{2,8.2}+\mathrm{2,9}+\mathrm{3,0}+\mathrm{3,1}+\mathrm{3,3.2}+\mathrm{3,5}+\mathrm{4,1}}{10}$= 3,13

Ta có bảng sau:

Mẫu số liệu gồm 10 giá trị nên n = 10. Do đó phương sai là: s2 = $\frac{\mathrm{1,821}}{10}$= 0,1821.

Độ lệch chuẩn là: s = $\sqrt{\mathrm{0,1821}}$≈ 0,4267.

Bài 2. Tỉ lệ thất nghiệp từ năm 2006 – 2020 tại Việt Nam (đơn vị %) được cho như sau:

0,00; 2,03; 0,00; 1,74; 1,11; 1,00; 1,03 ; 1,32; 1,26; 1,85; 1,85; 1,87; 1,16; 2,04; 2,39.

Hãy tìm các giá trị bất thường (nếu có) của mẫu số liệu trên.

Hướng dẫn giải

Sắp xếp các số liệu theo thứ tự không giảm ta có:

0,00; 0,00; 1,00; 1,03; 1,11; 1,16; 1,26; 1,32; 1,74; 1,85; 1,85; 1,87; 2,03; 2,04; 2,39.

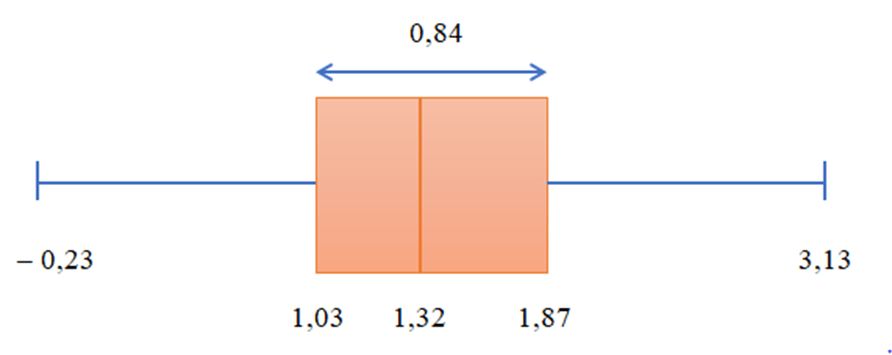
Từ mẫu số liệu trên, ta tính được Q2 = 1,32; Q1 = 1,03 và Q3 = 1,87. Do đó khoảng tứ phân vị là:

∆Q = Q3 – Q1 = 1,87 – 1,03 = 0,84.

Biểu đồ hộp cho mẫu số liệu này là:

Ta có Q1 – 1,5.∆Q = – 0,23 và Q3 + 1,5.∆Q = 3,13 nên trong mẫu số liệu trên không có giá trị nào được xem là bất thường.

Bài 3. Mỗi khẳng định sau đúng hay sai?

a) Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch chuẩn càng lớn;

b) Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất, bỏ qua thông tin của các giá trị còn lại;

c) Khoảng tứ phân vị có sử dụng thông tin của các giá trị lớn nhất và giá trị bé nhất;

d) Các số đo độ phân tán đều không âm.

Hướng dẫn giải

a) Sai.

Nếu các giá trị của mẫu số liệu đều tập trung quanh giá trị trung bình thì độ lệch của mỗi giá trị xi – $\overline{x}$càng nhỏ.

Ta suy ra (x­i­ – $\overline{x}$)2 cũng càng nhỏ.

Do đó tổng các bình phương độ lệch cũng càng nhỏ.

Mà độ lệch chuẩn tỉ lệ thuận với tổng các bình phương độ lệch.

Vậy trong trường hợp này, độ lệch chuẩn càng nhỏ.

b) Đúng.

Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất mà bỏ qua thông tin từ tất cả các giá trị khác. Do đó, khoảng biến thiên rất dễ bị ảnh hưởng bởi các giá trị bất thường.

c) Sai.

Khoảng tứ phân vị chỉ sử dụng 50% số liệu chính giữa của mẫu số liệu đã sắp xếp.Vậy khoảng biến thiên không sử dụng giá trị lớn nhất và giá trị bé nhất.

d) Đúng.

Khoảng biến thiên là hiệu của giá trị lớn nhất và giá trị bé nhất. Do đó khoảng biến thiên luôn không âm.

Khoảng tứ phân vị là hiệu của tứ phân vị thứ ba và tứ phân vị thứ nhất. Do đó khoảng tứ phân vị luôn không âm.

Phương sai là tổng các bình phương các độ lệch nên luôn không âm.

Độ lệch chuẩn là căn bậc hai của phương sai nên độ lệch chuẩn luôn không âm.