Lý thuyết Hệ thức lượng trong tam giác (Kết nối tri thức 2024) Toán 10

Lý thuyết Toán lớp 10 Chương 3: Hệ thức lượng trong tam giác

A. Lý thuyết Chương 3: Hệ thức lượng trong tam giác

1. Giá trị lượng giác của một góc

Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.

Cho trước một góc α, 0° ≤ α ≤ 180°. Khi đó, có duy nhất điểm M(x0; y0) trên nửa đường tròn đơn vị để $\widehat{\mathrm{xOM}}=\mathrm{\alpha }$.

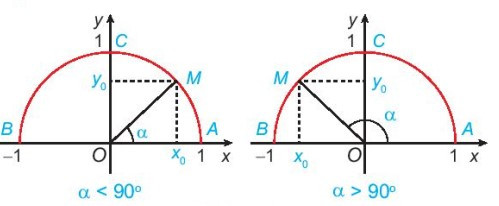
- Định nghĩa tỉ số lượng giác của một góc từ 00 đến 1800

Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho  $\widehat{\mathrm{xOM}}=\mathrm{\alpha }$. Khi đó:

+ sin của góc α là tung độ y0 của điểm M, được kí hiệu là sin α;

+ côsin của góc α là hoành độ x0  của điểm M, được kí hiệu là cos α;

+ Khi α ≠ 90° (hay x0 ≠ 0), tang của α là $\frac{{\mathrm{y}}_0}{{\mathrm{x}}_0}$, được kí hiệu là tan α;

+ Khi α ≠ 0° và α ≠ 180° (hay y0 ≠ 0), côtang của α là $\frac{{\mathrm{x}}_0}{{\mathrm{y}}_0}$, được kí hiệu là cot α.

- Từ định nghĩa trên ta có:

$\mathrm{tan\alpha }=\frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}(\mathrm{\alpha }\ne 90°);$$\mathrm{cot\alpha }=\frac{\mathrm{cos\alpha }}{\mathrm{sin\alpha }}(\mathrm{\alpha }\ne 0°\mathrm{và}\mathrm{\alpha }\ne 180°);$$\mathrm{tan\alpha }=\frac{1}{\mathrm{cot\alpha }}\text{ (}\mathrm{\alpha }\notin \text{{}0°;90°;180°\text{}})$

- Bảng giá trị lượng giác (GTLG) của một số góc đặc biệt:

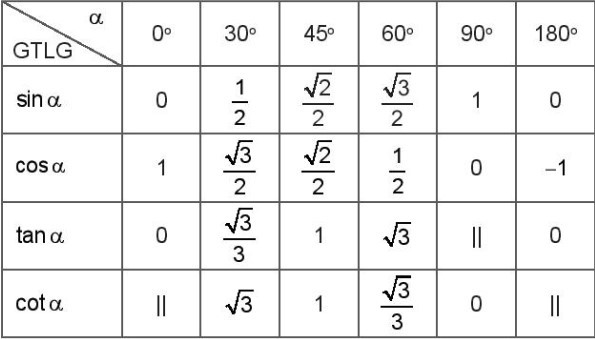
Chú ý: Kí hiệu || chỉ giá trị lượng giác tương ứng không xác định.

Ví dụ: Tìm các giá trị lượng giác của góc 120°.

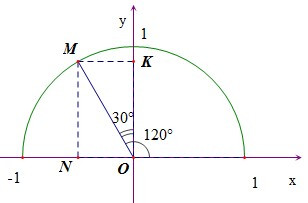
Gọi M là điểm trên nửa đường tròn đơn vị sao cho $\widehat{\mathrm{xOM}}={120}^0$. Gọi N, K tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Do $\widehat{\mathrm{xOM}}={120}^0$ và $\widehat{\mathrm{xOK}}={90}^0$nên $\widehat{\mathrm{KOM}}={30}^0$và $\widehat{\mathrm{MON}}={60}^0$.

Từ bảng GTLG của một số góc đặc biệt:

Ta có: cos 600 = $\frac{1}{2}$ và cos 300 = $\frac{\sqrt{3}}{2}$

Các tam giác MOK và MON là các tam giác vuông với cạnh huyền bằng 1

Suy ra ON = cos$\widehat{\mathrm{MON}}$.OM = cos600.1 = $\frac{1}{2}$ và OK = cos$\widehat{\mathrm{MOK}}$.OM = cos300.1 = $\frac{\sqrt{3}}{2}$

Mặt khác, do điểm M nằm bên trái trục tung nên $\mathrm{M}\left(-\frac{1}{2};\frac{\sqrt{3}}{2}\right)$

Theo định nghĩa giá trị lượng giác ta có:

sin 1200 = $\frac{\sqrt{3}}{2}$

cos 1200 =  $-\frac{1}{2}$

tan 1200 = $\frac{\sin {120}^0}{\cos {120}^0}=-\sqrt{3}$

cot 1200 = $\frac{\cos {120}^0}{\sin {120}^0}=-\frac{1}{\sqrt{3}}$.

Vậy sin 1200 = $\frac{\sqrt{3}}{2}$; cos 1200 =  $-\frac{1}{2}$; tan 1200 = $-\sqrt{3}$; cot 1200 = $-\frac{1}{\sqrt{3}}$.

- Ta có thể dùng máy tính bỏ túi để tính giá trị gần đúng của các giá trị lượng giác của một góc.

Ví dụ:

- Ta cũng có thể tìm được góc khi biết một giá trị lượng giác của góc đó.

Ví dụ:

 

Chú ý:

+ Khi tìm x biết sin x, máy tính chỉ đưa ra giá trị x ≤ 90°.

+ Muốn tìm x khi biết cos x, tan x, ta cũng làm tương tự như trên, chỉ thay phím  tương ứng bởi phím .

2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Đối với hai góc bù nhau, α và 180° – α, ta có:

sin (180° – α) = sin α;

cos (180° – α) = - cos α;

tan (180° – α) = - tan α  (α ≠ 90°);

cot (180° – α) = - cot α  (0° < α < 180°).

Chú ý:

- Hai góc bù nhau có sin bằng nhau ; có côsin , tang, côtang đối nhau.

Ví dụ: Tính các giá trị lượng giác của góc 135°.

Hướng dẫn giải

Ta có 135° + 45° = 180°, vì vậy góc 135° và góc 45° là hai góc bù nhau:

Suy ra:

sin135° = sin45° = $\frac{\sqrt{2}}{2}$

cos135° = - cos45° = $-\frac{\sqrt{2}}{2}$

tan135° = - tan45° = -1

cot135° = - cot45° = -1.

Vậy sin135° = $\frac{\sqrt{2}}{2}$; cos135° = $-\frac{\sqrt{2}}{2}$; tan35° = -1 ; cot135° = -1.

- Hai góc phụ nhau có sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Ví dụ:

Ta có  30° + 60° = 90° nên góc 30° và góc 60° là hai góc phụ nhau.

Khi đó: 

sin30° = cos60° = $\frac{1}{2}$

tan30° = cot60° = $\frac{\sqrt{3}}{3}$.

3. Định lí côsin 

Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.

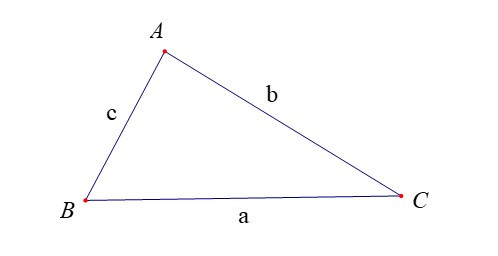
Định lí Côsin. Trong tam giác ABC:

a2 = b2 + c2 – 2bc.cosA.

b2 = c2 + a2 – 2ca.cosB.

c2 = a2 + b2 – 2ab.cosC.

Ví dụ: Cho tam giác ABC có góc A bằng 60° và AB = 2 cm, AC = 3 cm. Tính độ dài cạnh BC.

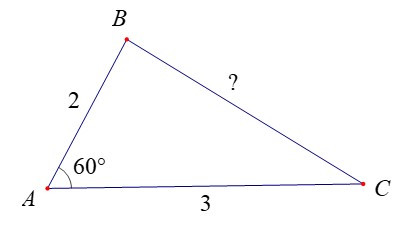
Hướng dẫn giải

Áp dụng Định lí côsin cho tam giác ABC, ta có:

BC2 = AB2 + AC2 – 2AB . AC . cos 600 = 22 + 32 – 2.2.3. $\frac{1}{2}$ = 7.

Suy ra BC = $\sqrt{7}$ (cm)

Vậy BC = $\sqrt{7}$ cm.

4. Định lí sin

Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.

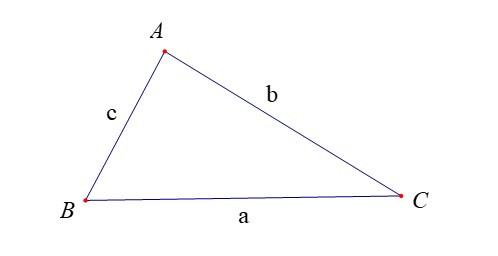
Định lí Côsin. Trong tam giác ABC:

a2 = b2 + c2 – 2bc.cosA.

b2 = c2 + a2 – 2ca.cosB.

c2 = a2 + b2 – 2ab.cosC.

Ví dụ: Cho tam giác ABC có góc A bằng 60° và AB = 2 cm, AC = 3 cm. Tính độ dài cạnh BC.

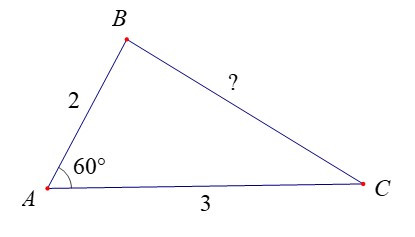
Hướng dẫn giải

Áp dụng Định lí côsin cho tam giác ABC, ta có:

BC2 = AB2 + AC2 – 2AB . AC . cos 600 = 22 + 32 – 2.2.3. $\frac{1}{2}$ = 7.

Suy ra BC = $\sqrt{7}$ (cm)

Vậy BC = $\sqrt{7}$ cm.

5. Giải tam giác và ứng dụng thực tế

- Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác.

Chú ý: Áp dụng định lí côsin, sin và sử dụng máy tính cầm tay, ta có thể tính (gần đúng) các cạnh và góc của một tam giác trong các trường hợp sau:

+ Biết hai cạnh và góc xen giữa.

+ Biết ba cạnh.

+ Biết một cạnh và hai góc kề.

Ví dụ: Giải tam giác ABC biết b = 12, $\widehat{\mathrm{C}}=60°$, $\widehat{\mathrm{A}}=100°$.

Hướng dẫn giải

Theo định lí tổng ba góc của tam giác, ta có: $\widehat{\mathrm{A}}+\widehat{\mathrm{B}}+\widehat{\mathrm{C}}=180°$.

Suy ra $\widehat{\mathrm{B}}=180°-(\widehat{\mathrm{A}}+\widehat{\mathrm{C}})=180°-(100°+60°)=20°$.

Áp dụng định lí sin, ta có: $\frac{\mathrm{a}}{\mathrm{sinA}}=\frac{\mathrm{b}}{\mathrm{sinB}}=\frac{\mathrm{c}}{\mathrm{sinC}}$

$\iff \frac{\mathrm{a}}{\sin 100°}=\frac{12}{\sin 20°}=\frac{\mathrm{c}}{\sin 60°}$

Suy ra:

$\mathrm{a}=\frac{12}{\sin 20°}\cdot \sin 100°\approx 34,6$

$\mathrm{c}=\frac{12}{\sin 20°}\cdot \sin 60°\approx 30,4$

Vậy tam giác ABC có: $\widehat{\mathrm{A}}=100°$, $\widehat{\mathrm{B}}=20°$, $\widehat{\mathrm{C}}=60°$; a ≈ 34,6 ;b = 12; c ≈ 30,4.

Ví dụ: Để đo khoảng cách giữa hai đầu C và A của một hồ nước người ta không thể đi trực tiếp từ C đến A, người ta tiến hành như sau: Chọn 1 điểm B sao cho đo được khoảng cách BC, BA và góc BCA. Sau khi đo, ta nhận được BC = 5m, BA = 12m, $\widehat{\mathrm{BCA}}={37}^0$. Tính khoảng cách AC (làm tròn kết quả đến hàng phần trăm).

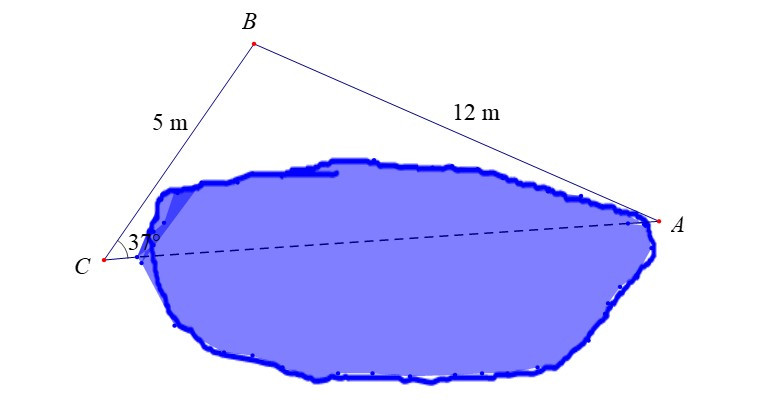
Hướng dẫn giải

Áp dụng định lí sin đối với tam giác ABC ta có:

$\frac{\mathrm{BC}}{\mathrm{sinA}}=\frac{\mathrm{AB}}{\mathrm{sinC}}$

⇒ $\frac{5}{\mathrm{sinA}}=\frac{12}{\sin {37}^0}$

⇒ sin A = $\frac{5.\sin {37}^0}{12}\approx 0,2508$

⇒ $\widehat{\mathrm{A}}$ ≈ 14°31’

⇒ $\widehat{\mathrm{B}}$ ≈ 180° – (37° + 14°31’) = 128°29’.

Áp dụng định lí sin, ta có: $\frac{\mathrm{AC}}{\mathrm{sinB}}=\frac{\mathrm{AB}}{\mathrm{sinC}}$ 

⇒ AC = $\frac{\mathrm{AB}}{\mathrm{sinC}}\cdot \mathrm{sinB}$ = $\frac{12}{\sin 37°}\cdot \sin 128°29\text{'}$ ≈15,61 (m)

Vậy khoảng cách AC ≈ 15,61 m.

6. Công thức tính diện tích tam giác

Đối với tam giác ABC: A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.

Ta có các công thức tính diện tích tam giác ABC sau:

+) S = pr = $\frac{(\mathrm{a}+\mathrm{b}+\mathrm{c})\mathrm{r}}{2}$

+) S = $\frac{1}{2}$bc sin A = $\frac{1}{2}$ca sin B =$\frac{1}{2}$ab sin C.

+) S = $\frac{\mathrm{abc}}{4\mathrm{R}}$

+) Công thức Heron: S = $\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$.

Ví dụ:

a) Tính diện tích tam giác ABC biết các cạnh b = 14 cm, c = 35 cm và $\widehat{\mathrm{A}}={60}^0$.

b) Tính diện tích tam giác ABC và bán kính đường tròn nội tiếp, ngoại tiếp tam giác ABC, biết các cạnh a = 4 cm, b =  5 cm, c = 3 cm.

Hướng dẫn giải

a) Áp dụng công thức tính diện tích tam giác ABC, ta có:

S = $\frac{1}{2}$bc sin A = $\frac{1}{2}$.14.35.sin 60° = $\frac{1}{2}$.14.35.$\frac{\sqrt{3}}{2}$=$\frac{245\sqrt{3}}{2}$(cm2).

Vậy diện tích tam giác ABC là: $\frac{245\sqrt{3}}{2}$ cm2.

b) Ta có nửa chu vi của tam giác ABC là: $\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}=\frac{4+5+3}{2}=\frac{12}{2}=6$ (cm).

Áp dụng công thức Heron, ta có diện tích tam giác ABC là:

S =$\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}=\sqrt{6.(6-4).(6-5).(6-3)}=\sqrt{36}=6$(cm2).

Mặt khác: S = $\frac{\mathrm{abc}}{4\mathrm{R}}$ ⇒ R = $\frac{\mathrm{abc}}{4\mathrm{S}}$= $\frac{4.5.3}{4.6}=\frac{5}{2}=2,5$ (cm).

Ta có: S = pr  ⇒ r = $\frac{\mathrm{S}}{\mathrm{p}}$ = $\frac{6}{6}$ = 1 (cm).

Vậy diện tích tam giác ABC là 6 cm2, bán kính đường tròn ngoại tiếp là 2,5 cm; bán kính đường tròn nội tiếp là 1 cm.

B. Bài tập tự luyện

B1. Bài tập tự luận

Bài 1. Cho góc α, biết sin α = $\frac{\sqrt{2}}{2}$. Tính giá trị của biểu thức A = 4sin2 α + 3cos2 α.

Hướng dẫn giải

Ta có:

A = 4sin2 α + 3cos2 α = (3sin2 α + 3cos2 α) + sin2 α = 3  (sin2 α + cos2 α) + sin2 α

Vì cos2 α  + sin 2 α  = 1 và sin α = $\frac{\sqrt{2}}{2}$.

Thay vào A ta có:  A = 3. 1 + ${\left(\frac{\sqrt{2}}{2}\right)}^2$ = $\frac{7}{2}$;

Vậy A = $\frac{7}{2}$.

Bài 2. Tính diện tích tam giác ABC biết a = 12  cm, b = 15 cm , c = 23 cm.

Hướng dẫn giải

Ta có $\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}=\frac{12+15+23}{2}=\frac{50}{2}=25$ (cm).

Áp dụng công thức Heron cho tam giác ABC ta có:

S = $\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$

S =$\sqrt{25.(25-12).(25-15).(25-23)}=\sqrt{6500}\approx 80,62$ (cm2).

Vậy diện tích tam giác ABC là 80,62 cm2.

Bài 3. Cho $\mathrm{A}=\frac{3\mathrm{sin\alpha }-\mathrm{cos\alpha }}{\mathrm{sin\alpha }+\mathrm{cos\alpha }}$ và tan α = $\sqrt{2}$. Chứng minh $\mathrm{A}=7-4\sqrt{2}.$ 

Hướng dẫn giải

Ta có $\mathrm{tan\alpha }=\frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}=\sqrt{2}\Rightarrow \mathrm{sin\alpha }=\sqrt{2}\mathrm{cos\alpha }$

Suy ra $\mathrm{A}=\frac{3\mathrm{sin\alpha }-\mathrm{cos\alpha }}{\mathrm{sin\alpha }+\mathrm{cos\alpha }}$

$=\frac{3\sqrt{2}\mathrm{cos\alpha }-\mathrm{cos\alpha }}{\sqrt{2}\mathrm{cos\alpha }+\mathrm{cos\alpha }}$ 

$=\frac{(3\sqrt{2}-1)\mathrm{cos\alpha }}{(\sqrt{2}+1)\mathrm{cos\alpha }}$

$=\frac{3\sqrt{2}-1}{\sqrt{2}+1}=\frac{\left(3\sqrt{2}-1\right)\left(\sqrt{2}-1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=7-4\sqrt{2}$

Vậy A= 7 –  4$\sqrt{2}$.

Bài 4. Tính giá trị của các biểu thức sau:

a) 3sin150° + tan135° + cot45°

b) cot135° – tan60°. cos230°

Hướng dẫn giải

a) 3sin 150° + tan 135° + cot 45°

= 3.sin(180° – 30°) + tan(180° – 45°) + cot 45°

= 3.sin30° –  tan45° + cot45°

= 3 . $\frac{1}{2}$ + (-1) + 1 = $\frac{3}{2}$.

b) cot 135° – tan 60°. cos2 30°  

= cot(180° – 45°) – tan60°.cos230°

= – cot45° – tan60°.cos230°

= (– 1) – $\sqrt{3}$.${\left(\frac{\sqrt{3}}{2}\right)}^2$= $-\frac{4+3\sqrt{3}}{4}$.

Bài 5.  Một hồ nước nằm ở góc tạo bởi hai con đường. Hãy tính khoảng cách từ B đến C, biết góc tạo bởi hai con đường là góc A bằng 120° và khoảng cách từ A đến B là 3 km, khoảng cách từ A đến C là 4 km.

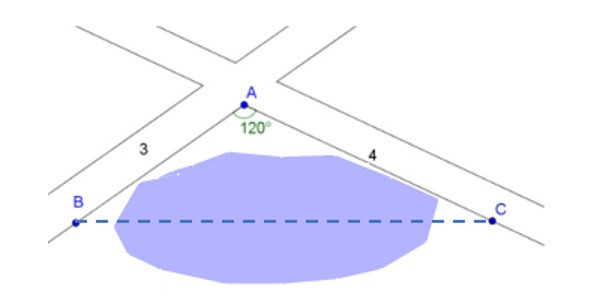
Hướng dẫn giải

Áp dụng định lí côsin cho tam giác ABC ta có:

BC2 = AB2 + AC2 – 2.AB.AC.cos A = 32 + 42 – 2. 3. 4 . cos 120° = 37.

⇒ BC = $\sqrt{37}$ ≈ 6,08 (km).

Vậy khoảng cách từ B đến C khoảng 6,08 km.

Bài 6. Giải tam giác ABC biết AB = 15, BC = 35, $\widehat{\mathrm{B}}=60°$. (Độ dài cạnh AC làm tròn đến chữ số thập phân thứ nhất, số đo góc A và C làm tròn đến độ).

Hướng dẫn giải

Áp dụng định lí côsin cho tam giác ABC, ta có:

AC2 = AB2 + BC2 – 2. AB. BC . cos B

= 152 + 352 – 2. 15. 35. cos 60° = 925.

Do đó AC = $\sqrt{925}$ ≈ 30,4.

Mặt khác:

BC2 = AB2 + AC2 – 2. AB. AC . cos A

⇒ cos A = $\frac{{\mathrm{AB}}^2+{\mathrm{AC}}^2-{\mathrm{BC}}^2}{2.\mathrm{AB}.\mathrm{AC}}$= $\frac{{15}^2+925-{35}^2}{\mathrm{2.15.}\sqrt{925}}\approx -0,08$.

⇒ $\widehat{\mathrm{A}}\approx 95°$

⇒ $\widehat{\mathrm{C}}=180°-(\widehat{\mathrm{A}}+\widehat{\mathrm{B}})\approx 180°-(95°+60°)=25°$

Vậy tam giác ABC có:

$\widehat{\mathrm{A}}\approx 95°$; $\widehat{\mathrm{B}}=60°$; $\widehat{\mathrm{C}}\approx 25°$.

AB = 15, AC  ≈ 30,4; BC = 35.

B2. Bài tập trắc nghiệm

Bài 1. Nếu 3cosx + 2 sinx = 2 và sinx < 0  thì giá trị đúng của

sinx là:

A. $-\frac{5}{13}$;

B. $-\frac{7}{13}$;

C. $-\frac{9}{13}$;

D. $-\frac{12}{13}$.

Hướng dẫn giải

Đáp án đúng là: A

Ta có: 3cosx + 2 sinx = 2

$\iff$(3cosx + 2 sinx)2 = 4

$\iff$9cos2x + 12cosx.sinx + 4sin2x = 4(sin2x + cos2x)

$\iff$5cos2x + 12cosx.sinx = 0

$\iff$cosx(5cosx + 12sinx) = 0

$\iff \left[\begin{array}{l}\text{cos}\mathrm{x}=0\\ 5\text{cos}\mathrm{x}+12\mathrm{sinx}=0\end{array}\right.$

Với cosx = 0$\Rightarrow$ sinx = 1 loại vì sinx < 0.

Với 5cosx + 12sinx = 0, ta có hệ phương trình: $\left\{\begin{array}{l}5\text{cos}\mathrm{x}+12\mathrm{sinx}=0\\ 3\mathrm{cosx}+2\mathrm{sinx}=2\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{sinx}=-\frac{5}{13}\\ \text{cos}\mathrm{x}=\frac{12}{13}\end{array}\right.$.

Vậy $\mathrm{sinx}=-\frac{5}{13}$.

Bài 2. Biết tanα = 2, giá trị của biểu thức $\mathrm{M}=\frac{3\mathrm{sin\alpha }-2\mathrm{cos\alpha }}{5\mathrm{cos\alpha }+7\mathrm{sin\alpha }}$

bằng:

A. $-\frac{4}{9}$;

B. $\frac{4}{19}$;

C. $-\frac{4}{19}$;

D. $\frac{4}{9}$.

Hướng dẫn giải

Đáp án đúng là: B

Cách 1: Vì cos α ≠ 0 nên chia cả tử và mẫu của M cho cosα ta có:

$\mathrm{M}=\frac{3\frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}-2}{5+7\frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}}=\frac{3.\mathrm{tan\alpha }-2}{5+7.\mathrm{tan\alpha }}=\frac{3.2-2}{5+7.2}=\frac{4}{19}$.

Cách 2: Ta có: $\mathrm{tan\alpha }=2\iff \frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}=2\left(\mathrm{cos\alpha }\ne 0\right)\iff \mathrm{sin\alpha }=2\mathrm{cos\alpha }$, thay sinα = 2cosα vào M ta được $\mathrm{M}=\frac{3.2\mathrm{cos\alpha }-2\mathrm{cos\alpha }}{5\mathrm{cos\alpha }+7.2\mathrm{cos\alpha }}=\frac{4\mathrm{cos\alpha }}{19\mathrm{cos\alpha }}=\frac{4}{19}$.

Bài 3. Cho $\mathrm{cos\alpha }=-\frac{4}{5}$ và góc α thỏa mãn 90° < α < 180°. Khi

đó.

A. $\mathrm{cot\alpha }=\frac{4}{3}$;

B. $\mathrm{sin\alpha }=\frac{3}{5}$;

C. $\mathrm{tan\alpha }=\frac{4}{5}$.

D. $\mathrm{sin\alpha }=-\frac{3}{5}$.

Hướng dẫn giải

Đáp án đúng là: B

Ta có sin2α + cos2α = 1

⇔ sin2α = 1 – cos2α  = 1 – ${\left(-\frac{4}{5}\right)}^2$= 1 – $\frac{16}{25}$= $\frac{9}{25}.$

⇔ $\left[\begin{array}{l}\mathrm{sin\alpha }=\frac{3}{5}\\ \mathrm{sin\alpha }=-\frac{3}{5}\end{array}\right.$

Vì 90° < α < 180° nên sinα > 0. Do đó $\mathrm{sin\alpha }=\frac{3}{5}$ 

⇒ tanα = $\frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}=-\frac{3}{4}$, cotα = $\frac{\mathrm{cos\alpha }}{\mathrm{sin\alpha }}=-\frac{4}{3}$.

Vậy đáp án đúng là B.