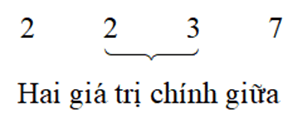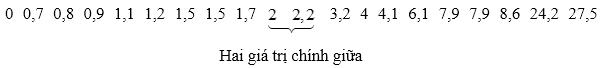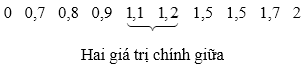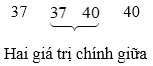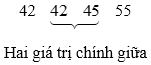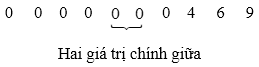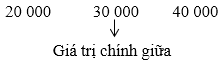Lý thuyết Các số đặc trưng đo xu thế trung tâm (Kết nối tri thức 2024) Toán 10

Lý thuyết Toán lớp 10 Bài 13: Các số đặc trưng đo xu thế trung tâm

A.Lý thuyết Các số đặc trưng đo xu thế trung tâm

1. Số trung bình và trung vị

a) Số trung bình

Số trung bình (số trung bình cộng) của mẫu số liệu x1, x2,..., xn, kí hiệu là $\overline{x}$được tính bằng công thức:

$\overline{x}=\frac{x_1+x_2+\mathrm{...}+x_n}{n}$

Ví dụ: Kết quả thống kê số điểm đạt được sau mỗi lần bắn của một xạ thủ được ghi lại trong bảng sau:

Tính điểm số trung bình qua các lần bắn của xạ thủ.

Hướng dẫn giải

Đếm số phát súng xạ thủ đã bắn trong bảng trên, ta thấy xạ thủ đã bắn tổng cộng là 10 phát. Ta suy ra n = 10.

Lần thứ nhất xạ thủ bắn được 7 điểm. Do đó ta có x1 = 7.

Lần thứ hai xạ thủ bắn được 9 điểm. Do đó ta có x2 = 9.

Tương tự, ta được x3 = 8, x4 = 9, x5 = 7, x6 = 10, x7 = 9, x8 = 9, x9 = 7, x10 = 8.

Suy ra, điểm số trung bình qua các lần bắn của xạ thủ là:

$\frac{7+9+8+9+7+10+9+9+7+8}{10}=\mathrm{8,3}$(điểm)

Chú ý:

Trong trường hợp mẫu số liệu cho dưới dạng bảng tần số thì số trung bình được tính theo công thức:

$\overline{x}=\frac{m_1{x}_1+m_2{x}_2+\mathrm{...}+m_k{x}_k}{n}$

trong đó mk là tần số của giá trị xk và n = m1 + m2 +...+ mk.

Ví dụ: Kết quả điều tra về số con của một số hộ gia đình trong một tổ dân phố được ghi lại trong bảng sau:

Hỏi trung bình mỗi hộ gia đình trong tổ dân phố có bao nhiêu con?

Hướng dẫn giải

Tổng số hộ gia đình là: n = 4 + 4 + 8 + 3 + 1 = 20 (hộ gia đình).

Trung bình mỗi hộ gia đình trong tổ dân số có số con là:

$\frac{0.4+1.4+2.8+3.3+4.1}{20}=\mathrm{1,65}$ (con)

Ý nghĩa: Số trung bình là giá trị trung bình cộng của các số trong mẫu số liệu, nó cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu.

b) Trung vị

Trong trường hợp mẫu số liệu có giá trị bất thường (rất lớn hoặc rất bé so với đa số các giá trị khác), người ta không dùng số trung bình để đo xu thế trung tâm mà dùng trung vị.

Để tìm trung vị (kí hiệu là Me) của một mẫu số liệu, ta thực hiện như sau:

+ Sắp xếp các giá trị trong mẫu số liệu theo thứ tự không giảm.

+ Nếu số giá trị của mẫu số liệu là số lẻ thì giá trị chính giữa của mẫu là trung vị. Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu.

Ví dụ: Theo dõi thời gian giải một bài toán của 4 học sinh, giáo viên nhận thấy có 2 em giải bài toán trong 2 phút; 1 em giải bài toán trong 3 phút và 1 em giải bài toán trong 7 phút. Hãy tìm số trung bình và trung vị của mẫu số liệu trên.

Hướng dẫn giải

+ Số trung bình là: $\frac{2.2+3.1+7.1}{4}=\mathrm{3,5}$(phút)

+ Trung vị:

Sắp xếp số liệu theo thứ tự không giảm:

Dãy trên có hai giá trị chính giữa lần lượt là 2 và 3.

Vậy trung vị của mẫu số liệu là: $\frac{2+3}{2}=\mathrm{2,5}$.

Nhận xét: Trong mẫu số liệu được sắp xếp trên, số phần tử ở bên trái trung vị và số phần tử ở bên phải trung vị bằng nhau và bằng 2. Một học sinh giải bài toán mất 7 phút cao hơn hẳn số trung bình, đây chính là giá trị bất thường. Nếu ta thay thời gian giải bài toán của học sinh giải mất 7 phút thành 8; 9; 10;... (phút) thì trung vị vẫn không thay đổi trong khi số trung bình sẽ thay đổi.

Ý nghĩa: Trung vị không bị ảnh hưởng bởi giá trị bất thường trong khi số trung bình bị ảnh hưởng bởi giá trị bất thường. Vì vậy, khi mẫu số liệu có giá trị bất thường, người ta thường dùng trung vị đại diện cho các số liệu thống kê.

Ví dụ: Đo chiều cao (đơn vị cm) của 9 học sinh lớp 10A và được kết quả như bảng sau:

Tìm số trung bình và trung vị của mẫu số liệu trên. Trong hai số đó, số nào phù hợp hơn để đại diện cho chiều cao của 9 học sinh lớp 10A?

Hướng dẫn giải

+ Số trung bình là:

$\frac{149+153+155+153+150+188+148+151+150}{9}=\mathrm{155,22}$(cm)

+ Trung vị:

Sắp xếp số liệu theo thứ tự không giảm:

Vậy trung vị của mẫu số liệu là: 151 (cm).

+ Giữa hai số trung bình và số trung vị như trên, số trung vị bằng 151 (cm) phù hợp hơn để đại diện cho chiều cao của 9 học sinh lớp 10A vì trong mẫu số liệu có một em học sinh có chiều cao 188cm, đây là giá trị bất thường.

2. Tứ phân vị

Tứ phân vị dùng để xác định ngưỡng để phân loại các số liệu có trong mẫu số liệu.

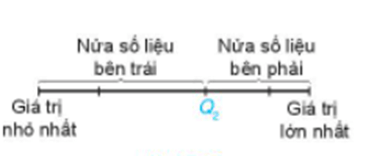
Để tìm các tứ phân vị của mẫu số liệu có n giá trị, ta làm như sau:

+ Sắp xếp mẫu số liệu theo thứ tự không giảm.

+ Tìm trung vị. Giá trị này là Q2.

+ Tìm trung vị của nửa số liệu bên trái Q2 (không bao gồm Q2 nếu n lẻ). Giá trị này là Q1.

+ Tìm trung vị của nửa số liệu bên phải Q2 (không bao gồm Q2 nếu n lẻ). Giá trị này là Q3.

Q1, Q2, Q3 được gọi là các tứ phân vị của mẫu số liệu.

Chú ý: Q1 được gọi là tứ phân vị thứ nhất hay tứ phân vị dưới, Q3 được gọi là tứ phân vị thứ ba hay tứ phân vị trên.

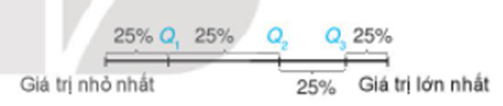
Ý nghĩa: Các điểm Q1, Q2, Q3 chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần đều chứa 25% giá trị.

Ví dụ: Hàm lượng Protein (đơn vị gam) trong 100g của một số loại thực phẩm được cho trong bảng sau:

Hãy tìm các tứ phân vị. Các tứ phân vị này cho ta thông tin gì?

Hướng dẫn giải

Sắp xếp các giá trị đã cho theo thứ tự không giảm:

+ Vì n = 20 là số chẵn nên Q2 là trung bình cộng của hai giá trị chính giữa. Do đó:

Q2 = (2 + 2,2) : 2 = 2,1.

+ Ta tìm Q1 là trung vị của nửa số liệu bên trái Q2:

Vì lúc này n = 10 là số chẵn nên Q1 là trung bình cộng của hai giá trị chính giữa. Do đó:

Q1 = (1,1 + 1,2) : 2 = 1,15.

+ Ta tìm Q3 là trung vị của nửa số liệu bên phải Q2:

Vì lúc này n = 10 là số chẵn nên Q3 là trung bình cộng của hai giá trị chính giữa. Do đó:

Q3 = (6,1 + 7,9) : 2 = 7.

Vậy các tứ phân vị của mẫu số liệu là Q1 = 1,15; Q2 = 2,1; Q3 = 7.

Các tứ phân vị cho ta hình ảnh phân bố của mẫu số liệu. Khoảng cách từ Q1 đến Q2 là 2,1 – 1,15 = 0,95 trong khi khoảng cách từ Q2 đến Q3 là 7 – 2,1 = 4,9. Điều này cho thấy mẫu số liệu tập trung với mật độ cao ở bên trái của Q2 và mật độ thấp ở bên phải của Q2.

3. Mốt

Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất.

Ý nghĩa: Có thể dùng mốt để đo xu thế trung tâm của mẫu số liệu khi mẫu số liệu có nhiều giá trị trùng nhau.

Ví dụ: Kết quả thống kê điểm số bài kiểm tra giữa kỳ của một số học sinh lớp 10B được cho trong bảng sau:

Tìm mốt cho mẫu số liệu này.

Hướng dẫn giải

Số học sinh đạt điểm 3: 1 học sinh.

Số học sinh đạt điểm 5: 1 học sinh.

Số học sinh đạt điểm 6: 1 học sinh.

Số học sinh đạt điểm 7: 3 học sinh.

Số học sinh đạt điểm 8: 2 học sinh.

Số học sinh đạt điểm 9: 1 học sinh.

Số học sinh đạt điểm 10: 1 học sinh.

Vì số học sinh đạt điểm 7 là lớn nhất (có 3 học sinh) nên mốt của mẫu số liệu này là 7.

Nhận xét:

+ Mốt có thể không là duy nhất. Chẳng hạn, với mẫu số liệu sau:

6959975595

Ta thấy các số 5; 9 đều xuất hiện với số lần lớn nhất (4 lần) nên mẫu số liệu này có hai mốt là 5 và 9.

+ Khi các giá trị trong mẫu số liệu xuất hiện với tần số như nhau thì mẫu số liệu không có mốt. Chẳng hạn, với mẫu số liệu sau:

686786778

Ta thấy các giá trị 6; 7; 8 trong mẫu số liệu đều xuất hiện với tần số như nhau (3 lần) nên mẫu số liệu này không có mốt.

+ Mốt còn được định nghĩa cho mẫu dữ liệu định tính (dữ liệu không phải là số). Ví dụ trong buổi biểu quyết chọn một trong ba bạn Hoa, Bình, Tú làm bí thư của lớp 10C, bạn thư ký của lớp đã tổng kết được kết quả biểu quyết như sau:

Trong mẫu dữ liệu này, số phiếu chọn “bạn Hoa” nhiều nhất, được gọi là mốt.

B. Bài tập tự luyện

Bài 1. Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:

a) Tuổi thọ (tính theo năm) của 6 loại bóng đèn được ghi lại như sau:

19 20 31 18 26 24

b) Số cân nặng (tính theo kg) của 9 học sinh lớp 10D được ghi lại như sau:

373740424540424255

Hướng dẫn giải

a) Tuổi thọ trung bình của 6 loại bóng đèn là:

$\frac{19+20+31+18+26+24}{6}$= 23 (năm)

+ Ta tìm trung vị của mẫu số liệu:

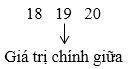
Sắp xếp các giá trị đã cho theo thứ tự không giảm:

Dãy trên có hai giá trị chính giữa lần lượt là 20 và 24.

Vậy trung vị của mẫu số liệu là: $\frac{20+24}{2}=22$.

+ Vì các giá trị 18; 19; 20; 24; 26; 31 trong mẫu số liệu đều xuất hiện với tần số như nhau (1 lần) nên mẫu số liệu này không có mốt.

+ Ta tìm tứ phân vị của mẫu số liệu:

Giá trị Q2 chính là trung vị của mẫu số liệu. Do đó ta có Q2 = 22.

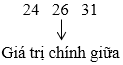
Ta tìm Q1 là trung vị của nửa số liệu bên trái Q2:

Giá trị chính giữa lúc này là 19. Ta suy ra Q1 = 19.

Ta tìm Q3 là trung vị của nửa số liệu bên phải Q2:

Giá trị chính giữa lúc này là 26. Ta suy ra Q3 = 26.

Vậy các tứ phân vị của mẫu số liệu là Q1 = 19; Q2 = 22; Q3 = 26.

b) Số cân nặng trung bình của 9 học sinh lớp 10D là:

$\frac{37.2+40.2+42.3+45+55}{6}\approx \mathrm{63,33}\left(kg\right)$

+ Ta tìm trung vị của mẫu số liệu:

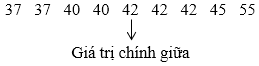
Sắp xếp các giá trị đã cho theo thứ tự không giảm:

Trung vị của mẫu số liệu là: 42.

+ Ta thấy giá trị 42 xuất hiện với tần số cao nhất (3 lần) nên mốt của mẫu số liệu này là 42.

+ Ta tìm tứ phân vị của mẫu số liệu:

Giá trị Q2 chính là trung vị của mẫu số liệu. Do đó ta có Q2 = 42.

Ta tìm Q1 là trung vị của nửa số liệu bên trái Q2:

Dãy trên có hai giá trị chính giữa là 37 và 40. Do đó Q1 = (37 + 40) : 2 = 38,5.

Ta tìm Q3 là trung vị của nửa số liệu bên phải Q2:

Dãy trên có hai giá trị chính giữa là 42 và 45. Do đó Q3 = (42 + 45) : 2 = 43,5.

Vậy các tứ phân vị của mẫu số liệu là Q1 = 38,5; Q2 = 42; Q3 = 43,5.

Bài 2. Số lượng học sinh giỏi Quốc gia năm học 2019 – 2020 của 10 trường Trung học phổ thông được cho như sau:

0 0 9 0 0 4 0 0 0 6

a) Tìm số trung bình, mốt và các tứ phân vị của mẫu số liệu trên.

b) Giải thích tại sao tứ phân vị thứ nhất và trung vị trùng nhau.

Hướng dẫn giải

a) Số lượng học sinh trung bình là: $\frac{0.7+9+4+6}{10}$= 1,9 (học sinh)

+ Ta tìm trung vị của mẫu số liệu:

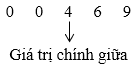
Sắp xếp các giá trị đã cho theo thứ tự không giảm:

Dãy trên có hai giá trị chính giữa cùng bằng 0.

Vậy trung vị của mẫu số liệu cũng bằng 0.

+ Ta thấy giá trị 0 xuất hiện với tần số cao nhất (7 lần) nên mốt của mẫu số liệu này là 0.

+ Ta tìm tứ phân vị của mẫu số liệu:

Giá trị Q2 chính là trung vị của mẫu số liệu. Do đó ta có Q2 = 0.

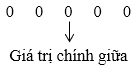
Ta tìm Q1 là trung vị của nửa số liệu bên trái Q2:

Giá trị chính giữa lúc này là 0. Ta suy ra Q1 = 0.

Ta tìm Q3 là trung vị của nửa số liệu bên phải Q2:

Giá trị chính giữa lúc này là 4. Ta suy ra Q3 = 4.

Vậy các tứ phân vị của mẫu số liệu là Q1 = 0; Q2 = 0; Q3 = 4.

b) Vì mẫu số liệu tập trung với mật độ cao ở bên trái Q2, tức là trung vị, nên tứ phân vị thứ nhất Q1 và trung vị Q2 trùng nhau.

Bài 3. Sức chứa của một số sân vận động tại Việt Nam đã được thống kê và ghi lại như trong bảng sau (số liệu gần đúng):

Các giá trị số trung bình, trung vị và mốt bị ảnh hưởng như thế nào nếu bỏ đi số liệu sức chứa của sân vận động Cần Thơ?

Hướng dẫn giải

+ Trước khi bỏ đi số liệu sức chứa của sân vận động Cần Thơ, ta có:

Sức chỗ ngồi trung bình là:

$\frac{40000+50000+30000+20000}{4}$ = 35 000.

Sắp xếp các giá trị đã cho theo thứ tự không giảm:

Dãy trên có hai giá trị chính giữa lần lượt là 30 000 và 40 000.

Do đó trung vị của mẫu số liệu là: $\frac{30000+40000}{2}$ = 35 000.

Trong mẫu dữ liệu trên, sức chứa ở sân vận động Cần Thơ là lớn nhất.

Do đó mốt của mẫu dữ liệu trên là “Cần Thơ”.

+ Sau khi bỏ đi số liệu sức chứa của sân vận động Cần Thơ, ta có:

Sức chỗ ngồi trung bình là:

$\frac{40000+30000+20000}{3}$ = 30 000.

Sắp xếp các giá trị đã cho theo thứ tự không giảm:

Dãy trên có giá trị chính giữa lần lượt là 30 000.

Do đó trung vị của mẫu số liệu là: 30 000.

Trong mẫu dữ liệu trên, sức chứa ở sân vận động Mỹ Đình là lớn nhất.

Do đó mốt của mẫu dữ liệu trên là “Mỹ Đình”.

+ Nếu bỏ đi số liệu sức chứa của sân vận động Cần Thơ, ta thấy:

Giá trị số trung bình và trung vị đều giảm 5000 (giảm từ 35 000 xuống còn 30 000).

Mốt của dữ liệu cũng bị thay đổi từ “Cần Thơ” sang “Mỹ Đình”.