Lý thuyết Hàm số (Kết nối tri thức 2024) Toán 10

Lý thuyết Toán 10 Bài 15: Hàm số

A. Lý thuyết Hàm số

1. Khái niệm hàm số

Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập hợp số thực ℝ thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D gọi là tập xác định của hàm số.

Tập tất cả các giá trị y nhận được, gọi là tập giá trị của hàm số.

Ví dụ : Viết hàm số mô tả sự phụ thuộc giữa diện tích S và bán kính r của hình tròn. Tìm tập xác định của hàm số đó.

Hướng dẫn giải

Diện tích S của hình tròn phụ thuộc vào bán kính r theo công thức S = π.r2, trong đó r là biến số, S = S(r) là hàm số của r.

Vì r là bán kính của hình tròn nên r > 0.

Do đó tập xác định của hàm số S = π.r2 là D = (0 ; +∞).

Vậy hàm số mô tả sự phụ thuộc giữa diện tích và bán kính của hình tròn là: S = S(r) = π.r2 và tập xác định của hàm số đó là: D = (0 ; +∞).

Chú ý : Khi cho hàm số bằng công thức y = f(x) mà không chỉ rõ tập xác định của nó thì ta quy ước tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

Ví dụ :

a) Tìm tập xác định của hàm y = $\sqrt{x+3}$

b) Tìm tập xác định của hàm y = $\frac{2x+4}{-x-1}$

Hướng dẫn giải

a) Biểu thức $\sqrt{x+3}$ có nghĩa khi x + 3 ≥ 0, tức là x ≥ – 3.

Vậy tập xác định của hàm số y = $\sqrt{x+3}$ là D = [– 3 ; +∞).

b) Biểu thức $\frac{2x+4}{-x-1}$ có nghĩa khi –x – 1 ≠ 0, tức là x ≠ –1.

Vậy tập xác định của hàm số y = $\frac{2x+4}{-x-1}$ là D = ℝ\{–1}.

Nhận xét : Một hàm số có thể cho bằng bảng, bằng biểu đồ, bằng công thức hoặc mô tả bằng lời.

Ví dụ :

a) Hàm số cho bởi công thức như hàm số y = f(x) = 2x + 7 ;

b) Nhiệt độ T(°C) tại các thời điểm t (giờ) trong cùng một ngày được cho bởi bảng sau :

Nhiệt độ T(°C) phụ thuộc vào sự thay đổi của thời gian t (giờ) và mỗi giờ chỉ tương ứng với đúng một giá trị nhiệt độ nên tương ứng đó xác định một hàm số.

Vậy bảng trên biểu thị một hàm số.

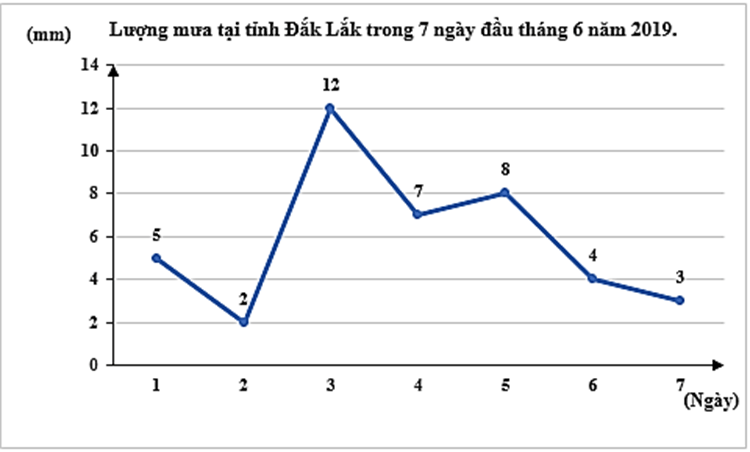
c) Cho biểu đồ sau:

Quan sát biểu đồ trên ta thấy ứng với mỗi ngày chỉ có đúng một giá trị lượng mưa nên tương ứng đó xác định một hàm số.

Vậy biểu đồ trên biểu thị một hàm số.

2. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x ; f(x)) trên mặt phẳng tọa độ với mọi x thuộc D.

Ví dụ: Tìm tập xác định và vẽ đồ thị của hàm số y = 2x trên mặt phẳng tọa độ.

Hướng dẫn giải

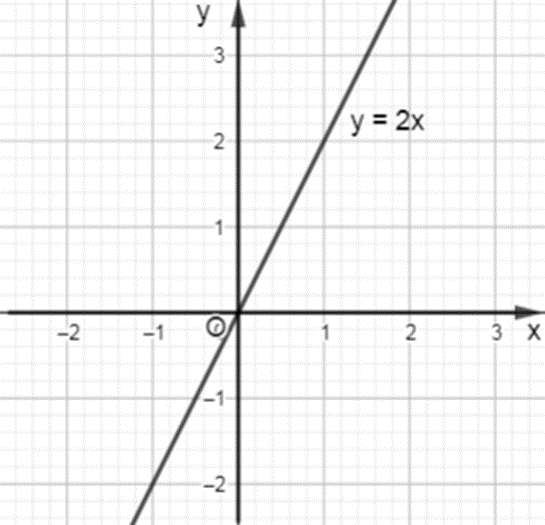
Vì 2x xác định với mọi x ∈ℝ nên tập xác định của hàm số y = 2x là D = ℝ.

Đồ thị của hàm số y = 2x là một đường thẳng đi qua gốc tọa độ như trong hình sau :

3. Sự đồng biến, nghịch biến của hàm số

- Hàm số y = f(x) được gọi là đồng biến (tăng) trên khoảng (a ; b), nếu

∀ x1, x2 ∈ (a ; b), x1 < x2 ⇒ f(x1) < f(x2).

- Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a ; b), nếu

∀ x1, x2 ∈ (a ; b), x1 < x2 ⇒ f(x1) > f(x2).

Chú ý:

- Đồ thị của một hàm số đồng biến trên khoảng (a; b) là đường “đi lên” từ trái sang phải;

- Đồ thị của một hàm số nghịch biến trên khoảng (a; b) là đường “đi xuống” từ trái sang phải.

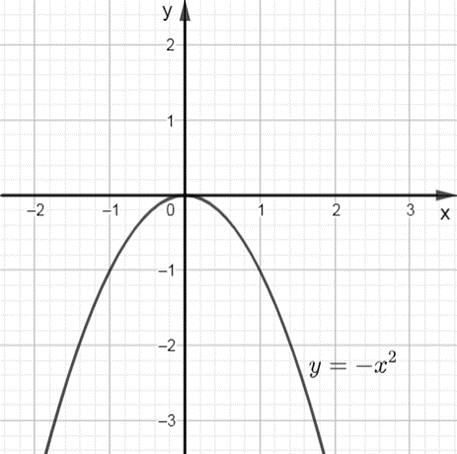
Ví dụ: Cho hàm số y = –x2 có đồ thị hàm số như hình sau:

Hàm số y = –x2 đồng biến hay nghịch biến trên mỗi khoảng (–∞; 0) và (0; +∞).

Hướng dẫn giải

Quan sát đồ thị hàm số y = –x2 ta thấy trên khoảng (–∞; 0), đồ thị đi lên từ trái sang phải. Do đó hàm số đồng biến trên khoảng (–∞; 0).

Ta thấy trên khoảng (0; +∞), đồ thị đi xuống từ trái sang phải. Do đó hàm số nghịch biến trên khoảng (0; +∞).

Vậy hàm số y = –x2 đồng biến trên khoảng (–∞; 0) và nghịch biến trên khoảng (0; +∞).

B. Bài tập Hàm số

Bài 1: Tìm tập xác định của hàm số sau :

a) y = $\sqrt{2x-3}$ + $\sqrt{3-x}$

b) y = $\frac{x}{-x^2+2x+3}$

c) y = $\frac{1}{2}$x + 5.

Hướng dẫn giải

a) Ta có $\sqrt{2x-3}$ xác định khi 2x – 3 ≥ 0 ⇔ x ≥ $\frac{3}{2}$

$\sqrt{3-x}$ xác định khi 3 – x ≥ 0 ⇔ x ≤ 3.

Khi đó $\sqrt{2x-3}$ + $\sqrt{3-x}$ xác định khi x ≥ $\frac{3}{2}$ và x ≤ 3, tức là x ∈ [1,5 ; 3].

Vậy tập xác định của hàm số y = $\sqrt{2x-3}$ + $\sqrt{3-x}$ là D = [1,5 ; 3].

b) Ta có $\frac{x}{-x^2+2x+3}$ xác định khi –x2 + 2x + 3 ≠ 0 ⇔ x ≠ –1 và x ≠ 3.

Do đó y = $\frac{x}{-x^2+2x+3}$ xác định khi x ≠ –1 và x ≠ 3.

Vậy tập xác định của hàm số y = $\frac{x}{-x^2+2x+3}$ là D = ℝ \{–1 ; 3}.

c) Ta có $\frac{1}{2}$x + 5 xác định với mọi x∈ℝ.

Vậy hàm số y = $\frac{1}{2}$x + 5 có tập xác định D = ℝ.

Bài 2: Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y là hàm số của x.

a) 2x + y = –4;

b) y = –x2;

c) x = y2 (với x > 0).

Hướng dẫn giải

a) Ta có 2x + y = –4 ⇔ y = –2x – 4

Ta thấy với mỗi giá trị của x thì chỉ xác định được tương ứng một giá trị của y theo công thức y = –2x – 4.

Do đó y = –2x – 4 là hàm số của x.

b) Ta có với mỗi giá trị của x thì xác định một giá trị của y theo công thức y = –x2.

Do đó y = –x2 là hàm số của x.

c) Từ x = y2 ⇔ y = $\sqrt{x}$ hoặc y = $-\sqrt{x}$ (với x > 0).

Do đó với một giá trị của x xác định hai giá trị của y.

Vậy x = y2 (với x > 0) không phải là hàm số của x.

Bài 3 : Vẽ đồ thị hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng :

a) y = 2x – 1

b) y = –3x2.

Hướng dẫn giải

a) Hàm số y = 2x – 1 có tập xác định D = ℝ

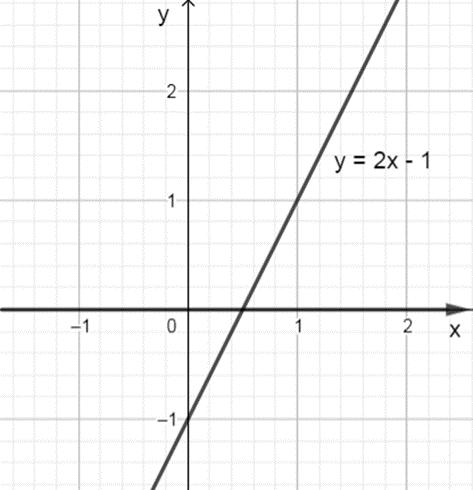
Đồ thị hàm số y = 2x – 1 là đường thẳng đi qua hai điểm (0 ; – 1) và (; 0) dưới hình vẽ sau :

Quan sát hình vẽ ta thấy đồ thì hàm số đi lên từ trái sang phải nên hàm số y = 2x – 1 đồng biến trên toàn tập xác định.

Vậy hàm số y = 2x – 1 đồng biến trên ℝ.

b) Hàm số y = –3x2 có tập xác định D = ℝ.

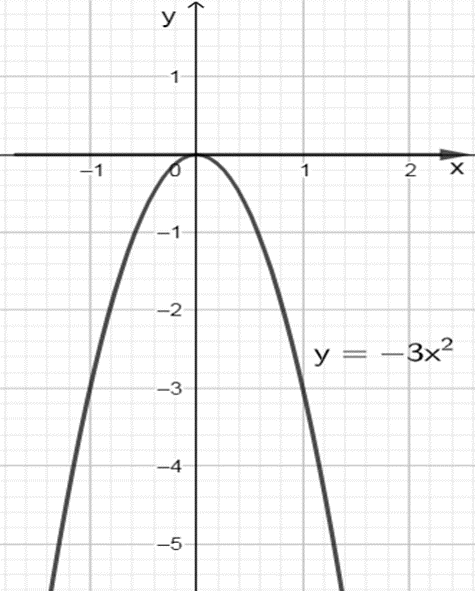
Đồ thị hàm số y = –3x2 là parabol trong hình vẽ sau :

Quan sát đồ thị hàm số y = –3x2 ta thấy trên khoảng (–∞; 0), đồ thị đi lên từ trái sang phải. Do đó hàm số đồng biến trên khoảng (–∞; 0).

Ta thấy trên khoảng (0; +∞), đồ thị đi xuống từ trái sang phải. Do đó hàm số nghịch biến trên khoảng (0; +∞).

Vậy hàm số y = –3x2 đồng biến trên khoảng (–∞; 0) và nghịch biến trên khoảng (0; +∞).

Bài 4 : Hiện tại bạn Lan đã để dành được một số tiền là 500 nghìn đồng. Bạn Lan muốn mua một chiếc xe đạp có giá 2 triệu đồng, nên hằng ngày Lan đều tiết kiệm 20 nghìn đồng. Gọi y là số tiền Lan tiết kiệm được sau x ngày.

a) Viết công thức liên hệ giữa y và x.

b) Hỏi sau bao nhiêu lâu kể từ ngày bắt đầu tiết kiệm thì Lan đủ tiền mua chiếc xe đạp đó.

Hướng dẫn giải

a) Vì mỗi ngày Lan tiết kiệm 20 nghìn đồng nên x ngày Lan tiết kiệm được số tiền là 20x (nghìn đồng).

Mặt khác ban đầu Lan đã có 500 nghìn đồng nên sau x ngày số tiền Lan có là: 500 + 20x (nghìn đồng).

Tức là số tiền Lan tiết kiệm được sau x ngày là y = 500 + 20x (nghìn đồng).

Vậy ta có công thức liên hệ giữa y và x là hàm số : y = 500 + 20x.

b)

Khi Lan đủ tiền mua chiếc xe đạp đó, tức là Lan đã tiết kiệm đủ 2 triệu đồng.

Khi đó y = 2 triệu đồng = 2 000 (nghìn đồng).

Thay y = 2 000 vào hàm số y = 500 + 20x ta được :

2 000 = 500 + 20x

⇔ 20x = 1 500

⇔ x = 75

Suy ra sau 75 ngày thì Lan tiết kiệm được 2 triệu đồng.

Vậy sau 75 ngày kể từ ngày bắt đầu tiết kiệm thì Lan đủ tiền mua chiếc xe đạp đó.