Lý thuyết Phương trình quy về phương trình bậc hai (Kết nối tri thức 2024) Toán 10

Lý thuyết Toán 10 Bài 18: Phương trình quy về phương trình bậc hai

A. Lý thuyết Phương trình quy về phương trình bậc hai

1. Phương trình dạng $\sqrt{a{x}^2+bx+c}=\sqrt{d{x}^2+ex+f}$

Để giải phương trình $\sqrt{a{x}^2+bx+c}=\sqrt{d{x}^2+ex+f}$ ta thực hiện như sau:

- Bình phương hai vế và giải phương trình nhận được;

- Thử lại các giá trị tìm được ở trên có thỏa mãn phương trình đã cho hay không và kết luận nghiệm.

Ví dụ: Giải phương trình $\sqrt{x^2-7x}=\sqrt{-x^2-8x+3}$

Hướng dẫn giải

Bình phương hai vế của phương trình $\sqrt{x^2-7x}=\sqrt{-x^2-8x+3}$ , ta được:

x2 – 7x = –x2 – 8x + 3

⇒ 2x2 + x – 3 = 0.

Giải phương trình 2x2 + x – 3 = 0 ta được x1 = 1 và x2 = $-\frac{3}{2}$ .

Thay lần lượt x1 = 1 và x2 = $-\frac{3}{2}$ vào ta thấy chỉ có giá trị x2 = $-\frac{3}{2}$ thỏa mãn.

Vậy phương trình có nghiệm là x = $-\frac{3}{2}$.

2. Phương trình dạng $\sqrt{a{x}^2+bx+c}=dx+e$ .

Để giải phương trình $\sqrt{a{x}^2+bx+c}=dx+e$ , ta thực hiện như sau:

- Bình phương hai vế và giải phương trình nhận được;

- Thử lại các giá trị tìm được ở trên có thỏa mãn phương trình đã cho hay không và kết luận nghiệm.

Ví dụ: Giải phương trình $\sqrt{4x^2+x-1}=-x+1$

Bình phương hai vế của phương trình , ta được:

4x2 + x – 1 = (–x + 1)2

⇒ 4x2 + x – 1 = x2 – 2x + 1

⇒ 3x2 + 3x – 2 = 0.

Giải phương trình 3x2 + 3x – 2 = 0 ta được $x_1=\frac{-3+\sqrt{33}}{6}$ và $x_2=\frac{-3-\sqrt{33}}{6}$

Thay lần lượt $x_1=\frac{-3+\sqrt{33}}{6}$ và $x_2=\frac{-3-\sqrt{33}}{6}$ vào $\sqrt{4x^2+x-1}=-x+1$ ta thấy cả hai giá trị $x_1=\frac{-3+\sqrt{33}}{6}$ và $x_2=\frac{-3-\sqrt{33}}{6}$ đều thỏa mãn.

Vậy phương trình có hai nghiệm là $x_1=\frac{-3+\sqrt{33}}{6}$ và $x_2=\frac{-3-\sqrt{33}}{6}$

B. Bài tập Phương trình quy về phương trình bậc hai

Bài 1: Giải các phương trình sau :

a) $\sqrt{x^2+x+2}=\sqrt{x^2-x+1}$

b) $\sqrt{x^2-2x}=\sqrt{-3x^2-x+1}$

Hướng dẫn giải

a) Bình phương hai vế của phương trình $\sqrt{x^2+x+2}=\sqrt{x^2-x+1}$ , ta được:

x2 + x + 2 = x2 – x + 1

⇒ 2x = – 1

⇒ x = $-\frac{1}{2}$

Thay x = $-\frac{1}{2}$ vào phương trình $\sqrt{x^2+x+2}=\sqrt{x^2-x+1}$ ta thấy thỏa mãn.

Vậy phương trình $\sqrt{x^2+x+2}=\sqrt{x^2-x+1}$ có nghiệm là x = $-\frac{1}{2}$ .

b) Bình phương hai vế của phương trình $\sqrt{x^2-2x}=\sqrt{-3x^2-x+1}$ , ta được:

x2 – 2x = –3x2 – x + 1

⇒ 4x2 – x – 1 = 0

Phương trình 4x2 – x – 1 = 0 có hai nghiệm phân biệt là

$x_1=\frac{1+\sqrt{17}}{8}$ và $x_2=\frac{1-\sqrt{17}}{8}$ .

Thay lần lượt $x_1=\frac{1+\sqrt{17}}{8}$ và $x_2=\frac{1-\sqrt{17}}{8}$vào phương trình $\sqrt{x^2-2x}=\sqrt{-3x^2-x+1}$ ta thấy chỉ có $x_2=\frac{1-\sqrt{17}}{8}$ thỏa mãn.

Vậy phương trình $\sqrt{x^2-2x}=\sqrt{-3x^2-x+1}$ có nghiệm là $x=\frac{1-\sqrt{17}}{8}$

Bài 2: Giải các phương trình sau:

a) $\sqrt{4x^2+3x+1}=-2x+1$

b) .$\sqrt{-x^2+2x+33}-x=-x+5$

Hướng dẫn giải

a) Bình phương hai vế của phương trình $\sqrt{4x^2+3x+1}=-2x+1$ , ta được:

4x2 + 3x + 1 = 4x2 – 4x + 1

⇒ 7x = 0

⇒ x = 0

Thay x = 0 vào phương trình $\sqrt{4x^2+3x+1}=-2x+1$ ta thấy thỏa mãn.

Vậy phương trình $\sqrt{4x^2+3x+1}=-2x+1$ có nghiệm là x = 0.

b) Ta có $\sqrt{-x^2+2x+33}-x=-x+5\iff \sqrt{-x^2+2x+33}=5$

Bình phương hai vế của phương trình $\sqrt{-x^2+2x+33}=5$ , ta được:

– x2 + 2x + 33 = 25

⇒ – x2 + 2x + 8 = 0

Phương trình –x2 + 2x + 8 = 0 có hai nghiệm phân biệt x1 = –2 và x2 = 4.

Thay lần lượt x1 = –2 và x2 = 4 vào phương trình $\sqrt{-x^2+2x+33}=5$ta thấy cả hai giá trị đều thỏa mãn.

Vậy phương trình $\sqrt{-x^2+2x+33}-x=-x+5$ có hai nghiệm là x1 = –2 và x2 = 4.

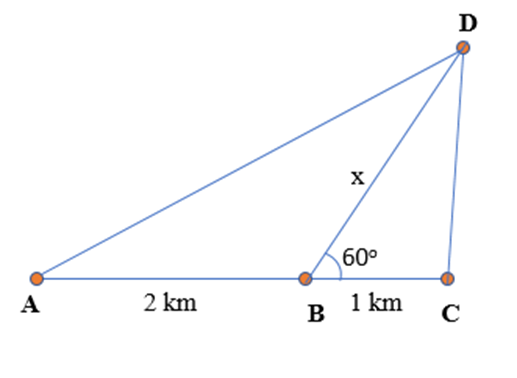
Bài 3: Nhà của An, Minh, Quân và Long lần lượt nằm trên các vị trí A, B, C, D như hình vẽ sau. Biết nhà An cách nhà Minh 2 km, nhà Minh cách nhà Quân 1 km. Biết khoảng cách từ nhà Long đến nhà Quân bằng $\frac{2}{3}$ khoảng cách từ nhà Long đến nhà An. Tính khoảng cách từ nhà Long đến nhà Minh.

Hướng dẫn giải

Gọi khoảng cách từ nhà Long đến nhà Minh là x (km), tức là DB = x km.

Nhà An cách nhà Minh 2 km nên AB = 2 km.

Nhà Minh cách nhà Quân 1 km nên BC = 1 km.

- Áp dụng định lí Côsin cho tam giác DBC ta có :

DC2 = DB2 + BC2 – 2.DB.BC.cos$\widehat{DBC}$ = x2 + 12 – 2.x.1.cos60° = x2 – x + 1

⇒ DC = $\sqrt{x^2-x+1}$ .

Suy ra khoảng cách từ nhà Long đến nhà Quân là $\sqrt{x^2-x+1}$ (km)

Ta có $\widehat{DBA}+\widehat{DBC}={180}^o$(hai góc kề bù)

Suy ra : $\widehat{DBA}={180}^o-\widehat{DBC}={180}^o-{60}^o={120}^o$.

- Áp dụng định lí Côsin cho tam giác DBA ta có :

AD2 = DB2 + AB2 – 2.DB.AB.cos$\widehat{DBA}$ = x2 + 22 – 2.x.2.cos120° = x2 + 2x + 4

⇒ AD = $\sqrt{x^2+2x+4}$.

Suy ra khoảng cách từ nhà Long đến nhà An là $\sqrt{x^2+2x+4}$ (km)

Do khoảng cách từ nhà Long đến nhà Quân bằng $\frac{2}{3}$ khoảng cách từ nhà Long đến nhà An nên ta có phương trình: $\sqrt{x^2-x+1}$ =$\frac{2}{3}$.$\sqrt{x^2+2x+4}$

Bình phương hai vế của phương trình $\sqrt{x^2-x+1}$=$\frac{2}{3}$ .$\sqrt{x^2+2x+4}$ ta được:

x2 – x + 1 = $\frac{4}{9}$(x2 + 2x + 4)

⇒ x2 – x + 1 = $\frac{4}{9}$x2 + $\frac{8}{9}$x + $\frac{16}{9}$

⇒ $\frac{5}{9}$x2 – $\frac{17}{9}$x – $\frac{7}{9}$ = 0.

Giải phương trình$\frac{5}{9}$ x2 –$\frac{17}{9}$ x – $\frac{7}{9}$ = 0 ta được x1 ≈ 3,8 và x2 ≈ – 0,4.

Vì x là khoảng cách từ nhà Long đến nhà Minh nên x > 0, do đó x2 ≈ – 0,4 không thỏa mãn.

Thay x1 ≈ 3,8 vào phương trình $\sqrt{x^2-x+1}$ = $\frac{2}{3}$. $\sqrt{x^2+2x+4}$ta thấy giá trị x1 ≈ 3,8 thỏa mãn.

Do đó phương trình $\sqrt{x^2-x+1}$ = $\frac{2}{3}$.$\sqrt{x^2+2x+4}$ có nghiệm là x ≈ 3,8.

Vậy khoảng cách từ nhà Long đến nhà Minh khoảng 3,8 km.