Lý thuyết Hàm số bậc hai (Kết nối tri thức 2024) Toán 10

Lý thuyết Toán 10 Bài 16: Hàm số bậc hai

A. Lý thuyết Hàm số bậc hai

1. Khái niệm hàm số bậc hai

Hàm số bậc hai là hàm số cho bởi công thức y = ax2 + bx + c, trong đó x là biến số, a, b, c là các hằng số và a ≠ 0.

Tập xác định của hàm số bậc hai là ℝ.

Nhận xét : Hàm số y = ax2 (a ≠ 0) đã học ở lớp 9 là một trường hợp đặc biệt của hàm số bậc hai với b = c = 0.

Ví dụ:

a) Hàm số y = 2x2 + x – 1 là hàm số bậc hai với a = 2, b = 1, c = –1.

b) Hàm số y = – x2 cũng là hàm số bậc hai với a = –1 và b = c = 0.

2. Đồ thị của hàm số bậc hai

- Đồ thị của hàm số bậc hai là một parabol.

- Đồ thị hàm số y = ax2 + bx + c (a ≠ 0) là một đường parabol có đỉnh là điểm $I\left(-\frac{b}{2a};-\frac{\Delta }{4a}\right)$, có trục đối xứng là đường thẳng $x=-\frac{b}{2a}$. Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0.

- Để vẽ đường parabol y = ax2 + bx + c ta tiến hành theo các bước sau :

1. Xác định tọa độ đỉnh $I\left(-\frac{b}{2a};-\frac{\Delta }{4a}\right)$ ;

2. Vẽ trục đối xứng $x=-\frac{b}{2a}$;

3. Xác định tọa độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol ;

4. Vẽ parabol.

Nhận xét : Từ đồ thị hàm số y = ax2 + bx + c (a ≠ 0), ta suy ra tính chất của hàm số y = ax2 + bx + c (a ≠ 0):

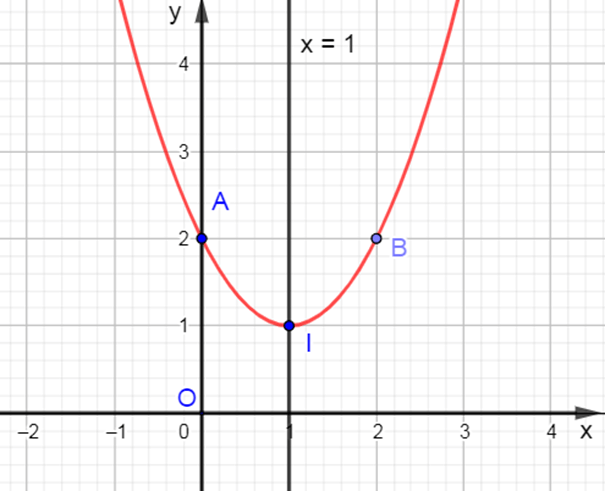
Ví dụ : Hãy vẽ parabol y = x2 – 2x + 2 và chỉ ra khoảng đồng biến, nghịch biến và giá trị nhỏ nhất của hàm số đó.

Hướng dẫn giải

Hàm số y = x2 – 2x + 2 có hệ số a = 1; b = – 2 ; c = 2.

Ta có : ∆ = (– 2)2 – 4.1.2 = –4.

Vì a = 1 > 0 nên parabol quay bề lõm lên trên.

Khi đó đỉnh $I=\left(-\frac{-2}{2.1};-\frac{-4}{4.1}\right)$ = (1 ; 1); trục đối xứng $x=-\frac{b}{2a}=-\frac{-2}{2.1}=1$.

Giao của đồ thị với trục Oy là A(0 ; 2).

Vì ∆ = – 4 < 0 nên phương trình x2 – 2x + 2 = 0 vô nghiệm, do đó đồ thị không giao với trục Ox.

Ta lấy điểm B(2; 2) đối xứng với A(0; 2) qua đường thẳng x = 1.

Ta có parabol y = x2 – 2x + 2 như hình vẽ sau :

b) Vì a = 1 > 0 nên ta có :

Hàm số y = x2 – 2x + 2 nghịch biến trên khoảng (–∞; 1);

Hàm số y = x2 – 2x + 2 đồng biến trên khoảng (1; +∞);

Giá trị nhỏ nhất của hàm số là y = 1, khi x = 1.

B. Bài tập Hàm số bậc hai

Bài 1: Xác định parabol y = ax2 + bx + c, biết parabol đi qua điểm A(4 ; 0) và có đỉnh là I(5 ; 7).

Hướng dẫn giải

Đỉnh của parabol là I(5 ; 7) do đó $-\frac{b}{2a}=5$ và 7 = a.52 + b.5 + c ⇒ 25a + 5b + c = 7.

Điểm A(4 ; 0) thuộc parabol nên ta có 0 = a.42 + b.4 + c ⇔ 16a + 4b + c = 0.

Khi đó, ta có hệ phương trình sau : $\left(\begin{array}{c}-\frac{b}{2a}=5\\ 25a+5b+c=7\\ 16a+4b+c=0\end{array}\right)$

Giải hệ trên ta được $\left(\begin{array}{c}a=-7\\ b=70\\ c=-168\end{array}\right)$

Vậy parabol cần tìm là y = –7x2 + 70x – 168.

Bài 2: Vẽ các parabol sau và xác định khoảng đồng biến, nghịch biến, giá trị lớn nhất, giá trị nhỏ nhất (nếu có).

a) y = x2 + 6x + 8

b) y = –x2 + 2x – 2

Hướng dẫn giải

a) Hàm số y = x2 + 6x + 8 có hệ số a = 1; b = 6 ; c = 8

Ta có : ∆ = 62 – 4.1.8 = 4

Vì a = 1 > 0 nên parabol quay bề lõm lên trên.

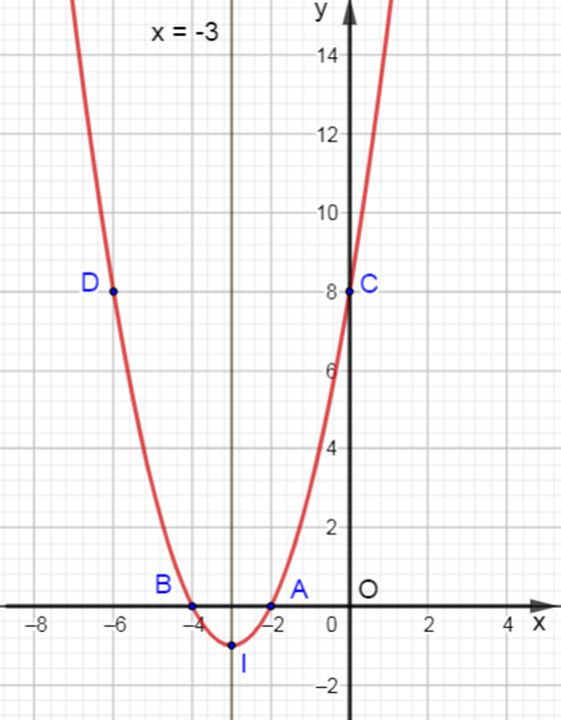
Khi đó đỉnh I = $\left(-\frac{6}{2.1};-\frac{4}{4.1}\right)$ = (–3 ; –1); trục đối xứng $x=-\frac{b}{2a}=-\frac{6}{2.1}=-3$;

Giao của đồ thị với trục Ox là A(–2 ; 0) và B(–4 ; 0)

Giao của đồ thị với trục Oy là C(0 ; 8)

Ta lấy thêm điểm D(–6 ; 8) đối xứng với C(0 ; 8) qua đường thẳng x = –3 , điểm D cũng thuộc parabol.

Khi đó, ta có parabol y = x2 + 6x + 8 như hình vẽ sau :

b) Hàm số y = –x2 + 2x – 2 có hệ số a = –1; b = 2 ; c = –2

Ta có : ∆ =22 – 4. (–1). (–2) = –4.

Vì a = –1 < 0 nên parabol quay bề lõm xuống dưới.

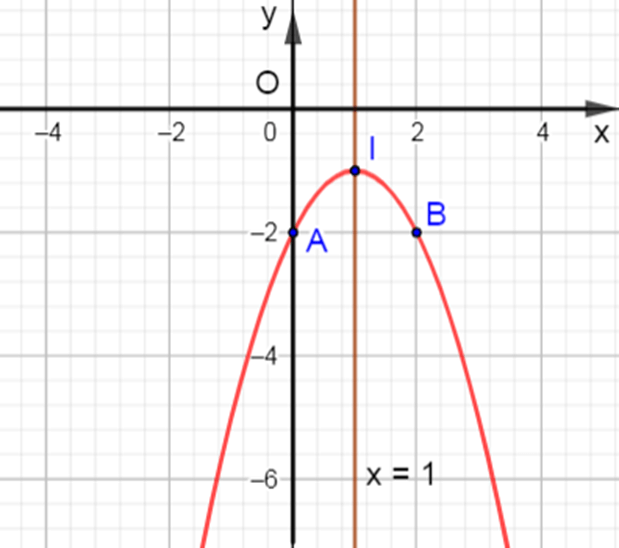
Khi đó đỉnh I =$\left(-\frac{2}{2.(-1)};-\frac{-4}{4.(-1)}\right)$ = (1 ; –1); trục đối xứng $x=-\frac{b}{2a}=-\frac{2}{2.(-1)}=1$.

Vì ∆ = –4 < 0 nên –x2 + 2x – 2 = 0 vô nghiệm, do đó đồ thị hàm số y = –x2 + 2x – 2 không cắt trục Ox.

Giao của đồ thị với trục Oy là A(0 ; –2)

Ta lấy thêm điểm B(2 ; –2) đối xứng với A(0 ; –2) qua đường thẳng x = 1, điểm B cũng thuộc parabol.

Khi đó, ta có parabol y = –x2 + 2x – 2 như hình vẽ sau :

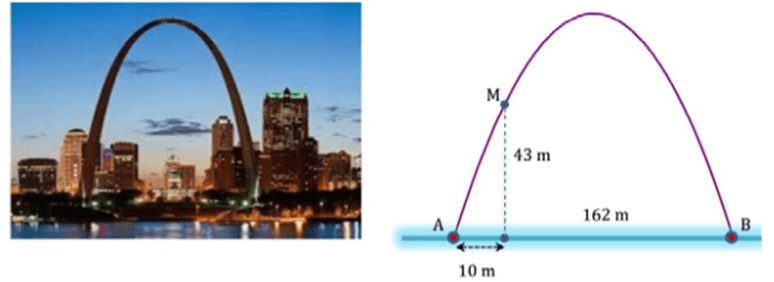
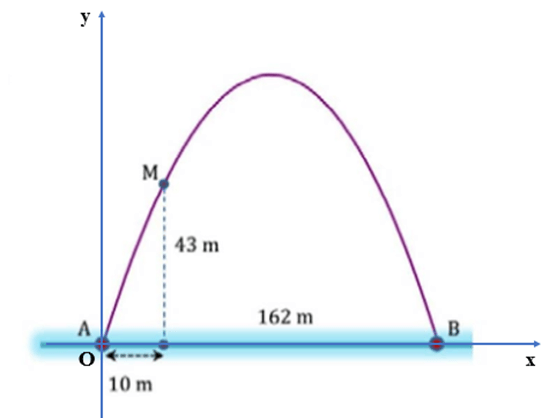
Bài 3 : Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất, người ta thả một sợi dây chạm đất, vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch.

Hướng dẫn giải

Ta chọn hệ trục tọa độ như hình sau:

Gọi phương trình của parabol cần tìm là y = ax2 + bx + c (a ≠ 0).

Khi đó parabol đi qua ba điểm A(0 ; 0), B(162 ; 0) và M(10 ; 43).

Thay lần lượt tọa độ các điểm này vào phương trình parabol. Khi đó ta có hệ phương trình sau :

$\left(\begin{array}{c}a{.0}^2+b.0+c=0\\ a{.162}^2+b.162+c=0\\ a{.10}^2+b.10+c=43\end{array}\right)$

Giải hệ trên :

$\left(\begin{array}{c}a{.0}^2+b.0+c=0\\ a{.162}^2+b.162+c=0\\ a{.10}^2+b.10+c=43\end{array}\right)$⇔ $\left(\begin{array}{c}c=0\\ a{.162}^2+b.162=0\\ a{.10}^2+b.10=43\end{array}\right)\iff \left(\begin{array}{c}c=0\\ a=-\frac{43}{1520}\\ b=\frac{3483}{760}\end{array}\right)$

Suy ra parabol cần tìm là y = $-\frac{43}{1520}$x2 + $\frac{3483}{760}$x.

Ta có ∆ = ${\left(\frac{3483}{760}\right)}^2-4.\left(-\frac{43}{1520}\right).0={\left(\frac{3483}{760}\right)}^2$

Khi đó chiều cao của cổng là h = $-\frac{\Delta }{4a}$ = $-\frac{{\left(\frac{3483}{760}\right)}^2}{4.\left(-\frac{43}{1520}\right)}$ ≈ 185,6 (m).

Vậy chiều cao của cổng Arch khoảng 185,6 mét.