Lý thuyết Vecto (Kết nối tri thức 2024) Toán 10

Lý thuyết Toán lớp 10 Chương 4: Vecto

A.Lý thuyết Chương 4: Vecto

1. Khái niệm vectơ

– Vectơ là một đoạn thẳng có hướng, nghĩa là, trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đầu, điểm cuối.

– Độ dài vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.

Chú ý:

+ Vectơ có điểm đầu A và điểm cuối B được kí hiệu là $\overrightarrow{AB}$, đọc là vectơ AB.

+ Để vẽ một vectơ, ta vẽ đoạn thẳng nối điểm đầu và điểm cuối của nó, rồi đánh dấu mũi tên ở điểm cuối.

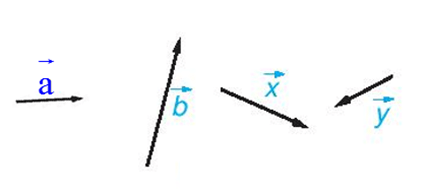
+ Vectơ còn được kí hiệu là $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{x}$, $\overrightarrow{y}$,…

+ Độ dài của vectơ $\overrightarrow{AB}$, $\overrightarrow{a}$tương ứng được kí hiệu là $\left|\overrightarrow{AB}\right|$, $\left|\overrightarrow{a}\right|$.

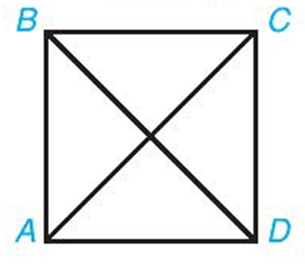
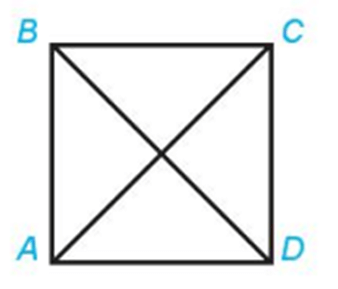
Ví dụ: Cho hình vuông ABCD với cạnh có độ dài bằng 1. Tính độ dài vectơ $\overrightarrow{AC}$, $\overrightarrow{BD}$.

Hướng dẫn giải

Vì ABCD là hình vuông nên $\hat{A}=\hat{B}=\hat{C}=\hat{D}=90°$.

Áp dụng định lý Pythagore cho tam giác ABD vuông tại A, có các cạnh góc vuông AB = AD = 1.

Ta có: BD2 = AB2 + AD2.

Suy ra: BD2 = 12 + 12 = 2 ⇒ BD = $\sqrt{2}$.

Do đó $\left|\overrightarrow{BD}\right|$= BD = $\sqrt{2}$

Mặt khác Vì ABCD là hình vuông nên hai đường chéo BD và AC bằng nhau.

Vì vậy AC = BD = $\sqrt{2}$

Do đó: $\left(\overrightarrow{AC}\right)$= AC = $\sqrt{2}$;

Vậy $\left|\overrightarrow{BD}\right|$= $\sqrt{2}$; $\left(\overrightarrow{AC}\right)$= $\sqrt{2}$

2. Hai vectơ cùng phương, cùng hướng, bằng nhau.

+ Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.

+ Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.

+ Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.

+ Hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ được gọi là bằng nhau, kí hiệu là $\overrightarrow{a}$ = $\overrightarrow{b}$, nếu chúng có cùng độ dài và cùng hướng.

Ví dụ:

Trong hình trên đường thẳng m đi qua điểm đầu và điểm cuối của vectơ $\overrightarrow{a}$, nên đường thẳng m gọi là giá của vectơ $\overrightarrow{a}$.

Tương tự, đường thẳng n là giá của hai vectơ $\overrightarrow{b}$ và $\overrightarrow{c}$.

Đường thẳng m và n song song với nhau nên ba vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ và là các vectơ cùng phương.

$\overrightarrow{a}$và $\overrightarrow{b}$cùng phương nhưng ngược hướng; $\overrightarrow{a}$ và $\overrightarrow{c}$cùng phương vàcùng hướng.

Hai vectơ $\overrightarrow{a}$và $\overrightarrow{c}$cùng hướng, ngoài ra chúng có độ dài bằng nhau nên $\overrightarrow{a}$= $\overrightarrow{c}$.

Chú ý:

+ Ta cũng xét các vectơ điểm đầu và điểm cuối trùng nhau (chẳng hạn $\overrightarrow{AA}$, $\overrightarrow{BB}$), gọi là các vectơ–không.

+ Ta quy ước vectơ–không có độ dài bằng 0, cùng hướng (do đó cùng phương) với mọi vectơ.

+ Các vectơ–không có cùng độ dài và cùng hướng nên bằng nhau và được kí hiệu chung là $\overrightarrow{0}$.

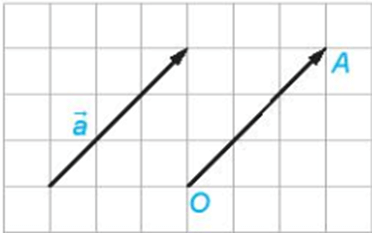
+ Với mỗi điểm O và vectơ $\overrightarrow{a}$cho trước, có duy nhất điểm A sao cho $\overrightarrow{OA}=\overrightarrow{a}$.

Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi $\overrightarrow{AB}$ và $\overrightarrow{AC}$cùng phương.

Chú ý: Ta có thể dùng vectơ để biểu diễn các đại lượng như lực, vận tốc, gia tốc. Hướng của vectơ chỉ hướng của đại lượng, độ dài của vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.

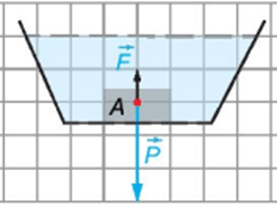
Ví dụ: Một vật A thả chìm hoàn toàn dưới đáy một cốc chất lỏng. Khi đó $\overrightarrow{F}$ biểu diễn lực đẩy Ác–si–mét và $\overrightarrow{P}$ biểu diễn trọng lực tác dụng lên vật A.

$\overrightarrow{F}$ và $\overrightarrow{P}$ tác dụng lên vật A theo phương thẳng đứng, hai lực này cùng phương nhưng ngược hướng. Do vật chìm hoàn toàn dưới đáy cốc nên trọng lực $\overrightarrow{P}$ có độ lớn lớn hơn lực đẩy Ác–si–mét $\overrightarrow{F}$, cụ thể $\left|\overrightarrow{P}\right|=3\left|\overrightarrow{F}\right|$.

3. Tổng của hai vectơ

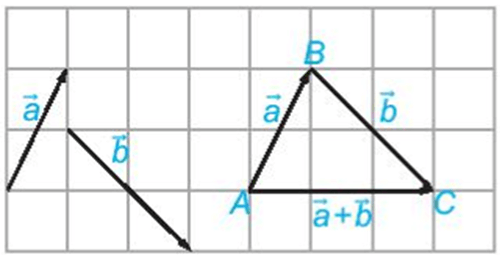
– Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$. Lấy một điểm A tùy ý và vẽ $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{BC}=\overrightarrow{b}$. Khi đó vectơ $\overrightarrow{AC}$được gọi là tổng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ và được kí hiệu là $\overrightarrow{a}$ + $\overrightarrow{b}$.

– Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

– Quy tắc ba điểm: Với ba điểm bất kì A, B, C, ta có $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ .

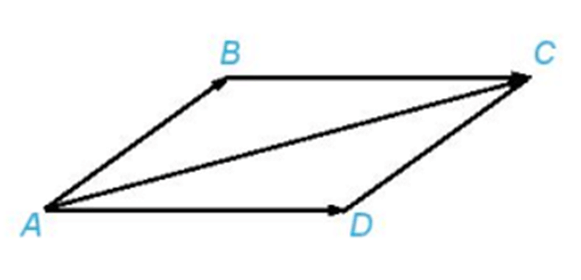
– Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.

– Với ba vectơ; $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ tùy ý :

+ Tính chất giao hoán: $\overrightarrow{a}$+ $\overrightarrow{b}$= $\overrightarrow{b}$ + $\overrightarrow{a}$;

+ Tính chất kết hợp: ($\overrightarrow{a}$ + $\overrightarrow{b}$) + $\overrightarrow{c}$ = $\overrightarrow{a}$ + ($\overrightarrow{b}$ + $\overrightarrow{c}$);

+ Tính chất của vectơ–không: $\overrightarrow{a}$ + $\overrightarrow{0}$ = $\overrightarrow{0}$+ $\overrightarrow{a}$ = $\overrightarrow{a}$.

Chú ý: Do các vectơ ($\overrightarrow{a}$ + $\overrightarrow{b}$) + $\overrightarrow{c}$ và $\overrightarrow{a}$ + ($\overrightarrow{b}$ + $\overrightarrow{c}$) bằng nhau, nên ta còn viết chúng dưới dạng $\overrightarrow{a}$ + $\overrightarrow{b}$ + $\overrightarrow{c}$ và gọi là tổng của ba vectơ $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$. Tương tự, ta cũng có thể viết tổng của một số vectơ mà không cần dùng dấu ngoặc.

Ví dụ: Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài của các vectơ $\overrightarrow{BC}+\overrightarrow{DC}$, $\overrightarrow{AB}+\overrightarrow{DC}+\overrightarrow{BD}$.

Hướng dẫn giải

Vì ABCD là hình vuông nên ta có $\overrightarrow{BC}=\overrightarrow{AD}$.

Khi đó $\overrightarrow{BC}+\overrightarrow{DC}$ = $\overrightarrow{AD}+\overrightarrow{DC}$ = $\overrightarrow{AC}$.

Suy ra : $|\overrightarrow{BC}+\overrightarrow{DC}|$ = $\left|\overrightarrow{AC}\right|$.

Mặt khác ABCD là hình vuông có các cạnh bằng 1 nên độ dài đường chéo AC = $\sqrt{2}$.

Và $\left|\overrightarrow{AC}\right|$ = AC, suy ra $\left|\overrightarrow{AC}\right|$ = $\sqrt{2}$.

Do đó $|\overrightarrow{BC}+\overrightarrow{DC}|$ = $\left|\overrightarrow{AC}\right|$= $\sqrt{2}$.

Ta có: $\overrightarrow{AB}+\overrightarrow{DC}+\overrightarrow{BD}$ = ($\overrightarrow{AB}$ + $\overrightarrow{BD}$) + $\overrightarrow{DC}$ = $\overrightarrow{AD}$ + $\overrightarrow{DC}$ = $\overrightarrow{AC}$.

Suy ra $|\overrightarrow{AB}+\overrightarrow{DC}+\overrightarrow{BD}|$ = $\left|\overrightarrow{AC}\right|=\sqrt{2}$.

Vậy $|\overrightarrow{BC}+\overrightarrow{DC}|$ = $\sqrt{2}$; $|\overrightarrow{AB}+\overrightarrow{DC}+\overrightarrow{BD}|$ = $\sqrt{2}$.

4. Hiệu của hai vectơ

– Vectơ có cùng độ dài và ngược hướng với vectơ $\overrightarrow{a}$ được gọi là vectơ đối của vectơ $\overrightarrow{a}$. Vectơ đối của vectơ $\overrightarrow{a}$ kí hiệu là –$\overrightarrow{a}$.

– Vectơ được coi là vectơ đối của chính nó.

– Hai vectơ đối nhau khi và chỉ khi tổng của chúng bằng $\overrightarrow{0}$.

– Vectơ $\overrightarrow{a}$+ (–$\overrightarrow{b}$) được gọi là hiệu của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ và được kí hiệu là $\overrightarrow{a}$– $\overrightarrow{b}$. Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.

– Nếu $\overrightarrow{b}$+ $\overrightarrow{c}$= $\overrightarrow{a}$ thì $\overrightarrow{a}$– $\overrightarrow{b}$ = $\overrightarrow{a}$+ (–$\overrightarrow{b}$) = $\overrightarrow{c}$ + $\overrightarrow{b}$+ (–$\overrightarrow{b}$) = $\overrightarrow{c}$+ $\overrightarrow{0}$ = $\overrightarrow{c}$.

– Quy tắc hiệu: Với ba điểm O, M, N, ta có $\overrightarrow{MN}=\overrightarrow{MO}+\overrightarrow{ON}=\left(-\overrightarrow{OM}\right)+\overrightarrow{ON}=\overrightarrow{ON}-\overrightarrow{OM}$.

Ví dụ: Cho hình bình hành ABCD và một điểm O bất kì. Chứng minh rằng $\overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{OC}-\overrightarrow{OD}$.

Hướng dẫn giải

Áp dụng quy tắc hiệu, ta có $\overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{AB}$; $\overrightarrow{OC}-\overrightarrow{OD}=\overrightarrow{DC}$.

Mặt khác, vì ABCD là hình bình hành nên $\overrightarrow{AB}=\overrightarrow{DC}$.

Vậy $\overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{OC}-\overrightarrow{OD}$.

Nhận xét: Trong vật lý, trọng tâm của một vật là điểm đặt của trọng lực tác dụng lên vật đó. Đối với một vật mỏng hình đa giác A1A2…An thì trọng tâm của nó là điểm G thỏa mãn $\overrightarrow{G{A}_1}+\overrightarrow{G{A}_2}+\mathrm{...}+\overrightarrow{G{A}_n}=\overrightarrow{0}$.

Ví dụ:

– Nếu I là trung điểm của đoạn thẳng AB thì $\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$

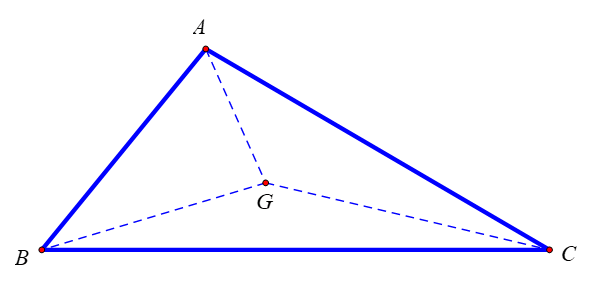
– Nếu G là trọng tâm của tam giác ABC thì $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Chú ý:

– Phép cộng tương ứng với các quy tắc tổng hợp lực, tổng hợp vận tốc:

+ Nếu hai lực cùng tác động vào chất điểm A và được biểu diễn bởi các vectơ $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ thì hợp lực tác động vào A được biểu diễn bởi vectơ $\overrightarrow{u_1}$ + $\overrightarrow{u_2}$.

+ Nếu một con thuyền di chuyển trên sông với vận tốc riêng (vận tốc so với dòng nước) được biểu diễn bở vectơ $\overrightarrow{v_r}$ và vận tốc của dòng nước (so với bờ) được biểu diễn bởi vectơ $\overrightarrow{v_n}$ thì vận tốc thực tế của thuyền (so với bờ) được biểu diễn bởi vectơ $\overrightarrow{v_r}$ + $\overrightarrow{v_n}$.

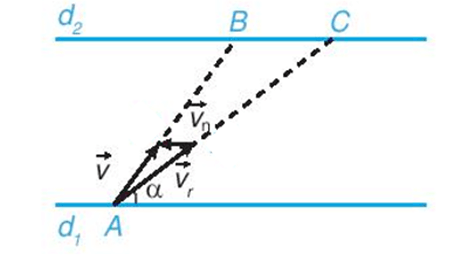
Ví dụ: Con tàu di chuyển từ bờ sông bên này sang bờ sông bên kia với vận tốc riêng không đổi. Vectơ vận tốc thực tế của tàu được biểu thị như sau:

Ta biểu thị hai bờ sông là hai đường thẳng d1, d2 song song với nhau. Giả sử tàu xuất phát từ A và bánh lái luôn giữ để tàu tạo với bờ góc α.

Gọi $\overrightarrow{v_r}$, $\overrightarrow{v_n}$ lần lượt là vectơ vận tốc riêng của tàu và vận tốc dòng nước.

Khi đó tàu chuyển động với vận tốc thực tế là: $\overrightarrow{v}=\overrightarrow{v_r}+\overrightarrow{v_n}$.

5. Tích của một vectơ với một số

• Tích của một vectơ $\overrightarrow{a}\ne \overrightarrow{0}$ với một số thực k > 0 là một vectơ, kí hiệu là k $\overrightarrow{a}$, cùng hướng với vectơ $\overrightarrow{a}$ và có độ dài bằng k $\overrightarrow{a}$.

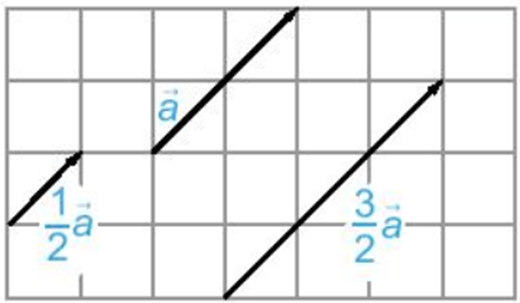
Ví dụ: Cho hình vẽ sau:

– Vectơ $\frac{1}{2}\overrightarrow{a}$ cùng hướng với vectơ $\overrightarrow{a}$ và $\left(\frac{1}{2}\overrightarrow{a}\right)$ = $\frac{1}{2}\left|\overrightarrow{a}\right|$

– Vectơ $\frac{3}{2}\overrightarrow{a}$ cùng hướng với vectơ $\overrightarrow{a}$ và $\left(\frac{3}{2}\overrightarrow{a}\right)$= $\frac{3}{2}\left|\overrightarrow{a}\right|$.

• Tích của một vectơ $\overrightarrow{a}\ne \overrightarrow{0}$ với một số thực k < 0 là một vectơ, kí hiệu là k $\overrightarrow{a}$, ngược hướng với vectơ $\overrightarrow{a}$ và có độ dài bằng (–k) |$\overrightarrow{a}$|.

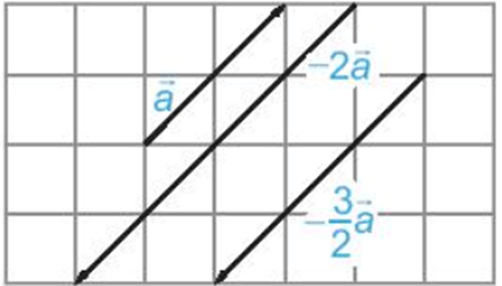
Ví dụ: Cho hình sau:

– Vectơ –2$\overrightarrow{a}$ ngược hướng với vectơ $\overrightarrow{a}$ và $\left(-2\overrightarrow{a}\right)$= $2\left|\overrightarrow{a}\right|$

– Vectơ $-\frac{3}{2}\overrightarrow{a}$ ngược hướng với vectơ $\overrightarrow{a}$ và $\left(-\frac{3}{2}\overrightarrow{a}\right)$= $\frac{3}{2}\left|\overrightarrow{a}\right|$.

Chú ý: Ta quy ước k $\overrightarrow{a}$ = $\overrightarrow{0}$ nếu $\overrightarrow{a}$ = $\overrightarrow{0}$ hoặc k = 0.

Nhận xét: Vectơ k $\overrightarrow{a}$ có độ dài bằng |k||$\overrightarrow{a}$| và cùng hướng với $\overrightarrow{a}$ nếu k ≥ 0, ngược hướng với $\overrightarrow{a}$ nếu $\overrightarrow{a}$ ≠ $\overrightarrow{0}$ và k < 0.

Chú ý: Phép lấy tích của vectơ với một số gọi là phép nhân vectơ với một số (hay phép nhân một số với vectơ).

6. Các tính chất của phép nhân vectơ với một số

Với hai vectơ $\overrightarrow{a}$, $\overrightarrow{b}$ và hai số thực k, t, ta luôn có :

+) k(t$\overrightarrow{a}$) = (kt) $\overrightarrow{a}$;

+) k ($\overrightarrow{a}$ + $\overrightarrow{b}$) = k$\overrightarrow{a}$ + k$\overrightarrow{b}$; k ($\overrightarrow{a}$ – $\overrightarrow{b}$) = k$\overrightarrow{a}$ – k$\overrightarrow{b}$;

+) (k + t) $\overrightarrow{a}$ = k$\overrightarrow{a}$ + t$\overrightarrow{a}$;

+) 1$\overrightarrow{a}$ = $\overrightarrow{a}$; (–1) $\overrightarrow{a}$ = –$\overrightarrow{a}$.

Nhận xét:

Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi $\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$.

Điểm G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Ví dụ:

a) Cho đoạn thẳng CD có trung điểm I. Chứng minh với điểm O tùy ý, ta có $\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OI}$.

b) Cho tam giác ABC có G là trọng tâm. Chứng minh rằng với điểm O tùy ý, ta có $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=3\overrightarrow{OG}$.

Hướng dẫn giải

a) Vì I là trung điểm của CD nên ta có $\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}$.

Do đó $\overrightarrow{OC}+\overrightarrow{OD}=(\overrightarrow{OI}+\overrightarrow{IC})+(\overrightarrow{OI}+\overrightarrow{ID})$ = 2$\overrightarrow{OI}$ + ($\overrightarrow{IC}+\overrightarrow{ID}$)= 2$\overrightarrow{OI}$ + $\overrightarrow{0}$ = 2$\overrightarrow{OI}$.

Vậy, $\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OI}$.

b) Vì G là trọng tâm tam giác ABC nên: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Ta có $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=(\overrightarrow{OG}+\overrightarrow{GA})+(\overrightarrow{OG}+\overrightarrow{GB})+(\overrightarrow{OG}+\overrightarrow{GC})$

= $3\overrightarrow{OG}+(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC})=3\overrightarrow{OG}+\overrightarrow{0}=3\overrightarrow{OG}$

Vậy $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}$.

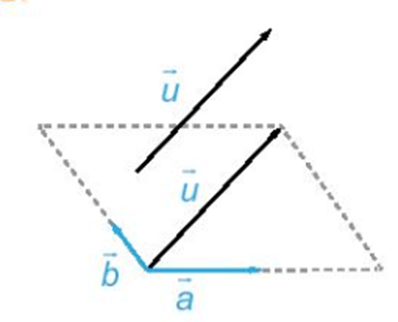
Chú ý : Cho hai vectơ không cùng phương $\overrightarrow{a}$ và $\overrightarrow{b}$. Khi đó, mọi vectơ $\overrightarrow{u}$ đều biểu thị (phân tích) được một cách duy nhất theo hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, nghĩa là có duy nhất cặp số (x; y) sao cho $\overrightarrow{u}$ = x$\overrightarrow{a}$ + y$\overrightarrow{b}$.

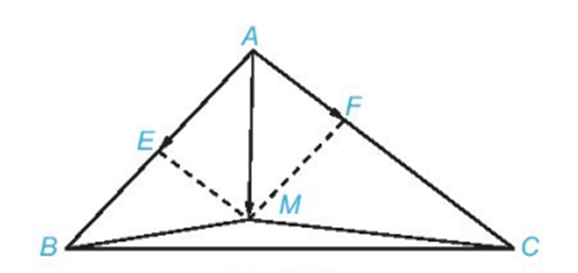
Ví dụ : Cho tam giác ABC. Hãy xác định điểm M để $\overrightarrow{MA}+3\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$.

Hướng dẫn giải

Để xác định vị trí của M, trước hết ta biểu thị $\overrightarrow{AM}$ (với gốc A đã biết) theo hai vectơ đã biết $\overrightarrow{AB},\overrightarrow{AC}$.

$\overrightarrow{MA}+3\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$

⇔ $\overrightarrow{MA}+3(\overrightarrow{MA}+\overrightarrow{AB})+2(\overrightarrow{MA}+\overrightarrow{AC})=\overrightarrow{0}$

⇔ $6\overrightarrow{MA}+3\overrightarrow{AB}+2\overrightarrow{AC}=\overrightarrow{0}$

⇔ $\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$

Lấy điểm E là trung điểm của AB và điểm F thuộc cạnh AC sao cho $\text{AF}=\frac{1}{3}AC$.

Khi đó $\overrightarrow{AE}=\frac{1}{2}\overrightarrow{AB}$ và $\overrightarrow{AF}=\frac{1}{3}\overrightarrow{AC}$. Vì vậy $\overrightarrow{AM}=\overrightarrow{AE}+\overrightarrow{AF}$.

Suy ra M là đỉnh thứ tư của hình bình hành EAFM.

7. Góc giữa hai vectơ

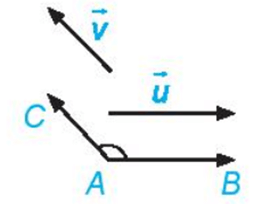
Cho hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ khác $\overrightarrow{0}$. Từ một điểm A tùy ý, vẽ các vectơ $\overrightarrow{AB}=\overrightarrow{u}$ và $\overrightarrow{AC}=\overrightarrow{v}$. Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ hay đơn giản là góc giữa hai vectơ $\overrightarrow{u}$, $\overrightarrow{v}$, kí hiệu là ($\overrightarrow{u}$, $\overrightarrow{v}$).

Chú ý :

+ Quy ước rằng góc giữa hai vectơ $\overrightarrow{u}$ và $\overrightarrow{0}$ có thể nhận một giá trị tùy ý từ 0° đến 180°.

+ Nếu ($\overrightarrow{u}$, $\overrightarrow{v}$) = 90° thì ta nói rằng $\overrightarrow{u}$ và $\overrightarrow{v}$ vuông góc với nhau. Kí hiệu $\overrightarrow{u}$ ⊥ $\overrightarrow{v}$ hoặc $\overrightarrow{v}$ ⊥ $\overrightarrow{u}$. Đặc biệt được coi là vuông góc với mọi vectơ.

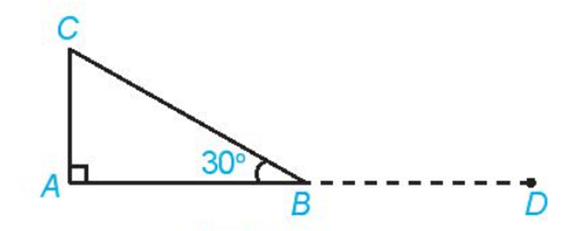
Ví dụ : Cho tam giác ABC vuông tại A và $\hat{B}=30°$. Tính $(\overrightarrow{AB},\overrightarrow{AC})$, $(\overrightarrow{CA},\overrightarrow{CB})$, $(\overrightarrow{AB},\overrightarrow{BC})$.

Hướng dẫn giải

Ta có $(\overrightarrow{AB},\overrightarrow{AC})$ = $\widehat{BAC}=90°$.

Tam giác ABC vuông tại A nên ta có .

$\widehat{ACB}+\widehat{ABC}=90°\Rightarrow \widehat{ACB}=90°-\widehat{ABC}=90°-30°=60°$

Suy ra: $(\overrightarrow{CA},\overrightarrow{CB})=\widehat{ACB}=60°$.

Vẽ $\overrightarrow{BD}$ sao cho $\overrightarrow{BD}$ = $\overrightarrow{AB}$. Khi đó $(\overrightarrow{AB},\overrightarrow{BC})$ = $(\overrightarrow{BD},\overrightarrow{BC})$ = $\widehat{CBD}$.

Mặt khác $\widehat{ABC}+\widehat{CBD}=180°$ (hai góc kề bù)

Suy ra $\widehat{CBD}=180°-\widehat{ABC}=180°-30°=150°$.

Do đó, $(\overrightarrow{AB},\overrightarrow{BC})$ = $\widehat{CBD}$ = 150°.

Vậy $(\overrightarrow{AB},\overrightarrow{AC})$ = 90°, $(\overrightarrow{CA},\overrightarrow{CB})$ = 60°, $(\overrightarrow{AB},\overrightarrow{BC})$ = 150°.

8. Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ khác vectơ-không $\overrightarrow{u}$ và $\overrightarrow{v}$ là một số, kí hiệu là $\overrightarrow{u}$.$\overrightarrow{v}$, được xác định bởi công thức sau:

$\overrightarrow{u}$. $\overrightarrow{v}$ = |$\overrightarrow{u}$|.|$\overrightarrow{v}$|.cos($\overrightarrow{u}$, $\overrightarrow{v}$)

Chú ý:

+) $\overrightarrow{u}$ ⊥ $\overrightarrow{v}$ ⇔ $\overrightarrow{u}$. $\overrightarrow{v}$ = 0.

+) $\overrightarrow{u}$. $\overrightarrow{u}$ còn được viết là ${\overrightarrow{u}}^2$ và được gọi là bình phương vô hướng của vectơ $\overrightarrow{u}$.

Ta có ${\overrightarrow{u}}^2=\left|\overrightarrow{u}\right|.\left|\overrightarrow{u}\right|.\cos 0°={\left(\overrightarrow{u}\right)}^2$.

(Bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó.)

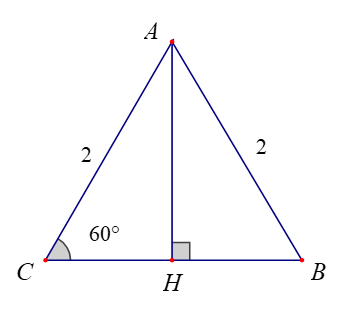
Ví dụ: Cho tam giác đều ABC có cạnh bằng 2 và có đường cao AH. Tính các tích vô hướng:

a) $\overrightarrow{AB}.\overrightarrow{AC}$;

b) $\overrightarrow{AH}.\overrightarrow{BC}$.

Hướng dẫn giải

a) Vì tam giác ABC đều nên $(\overrightarrow{AB},\overrightarrow{AC})=\widehat{BAC}=60°$.

Suy ra: $\overrightarrow{AB}.\overrightarrow{AC}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|\cos (\overrightarrow{AB},\overrightarrow{AC})=\mathrm{2.2.}\cos 60°=\mathrm{2.2.}\frac{1}{2}=2$.

Vậy $\overrightarrow{AB}.\overrightarrow{AC}$ = 2.

b) Vì AH là đường cao của tam giác ABC nên AH ⊥ BC.

Do đó $(\overrightarrow{AH},\overrightarrow{BC})=90°$.

Ta có: $\overrightarrow{AH}.\overrightarrow{BC}=\left|\overrightarrow{AH}\right|.\left|\overrightarrow{BC}\right|\cos (\overrightarrow{AH},\overrightarrow{BC})=\left|\overrightarrow{AH}\right|.\left|\overrightarrow{BC}\right|\cos 90°=\left|\overrightarrow{AH}\right|.\left|\overrightarrow{BC}\right|.0=0$.

Vậy $\overrightarrow{AH}.\overrightarrow{BC}$ = 0.

9. Biểu thức tọa độ và tính chất của tích vô hướng

• Tích vô hướng của hai vectơ $\overrightarrow{u}=(x;y)$ và $\overrightarrow{v}=(x\text{'};y\text{'})$ được tính theo công thức :

$\overrightarrow{u}$. $\overrightarrow{v}$ = x.x' + y.y'.

Nhận xét:

+ Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ vuông góc với nhau khi và chỉ khi x.x' + y.y' = 0.

+ Bình phương vô hướng của $\overrightarrow{u}=(x;y)$ là ${\overrightarrow{u}}^2$ = x2 + y2.

+ Nếu $\overrightarrow{u}$ ≠ $\overrightarrow{0}$ và $\overrightarrow{v}$ ≠ $\overrightarrow{0}$ thì cos($\overrightarrow{u}$, $\overrightarrow{v}$) = $\frac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\frac{xx\text{'}+yy\text{'}}{\sqrt{x^2+y^2}.\sqrt{x{\text{'}}^2+y{\text{'}}^2}}$.

Ví dụ: Trong mặt phẳng tọa độ cho hai vectơ $\overrightarrow{u}=(0;-5)$ và $\overrightarrow{v}=(\sqrt{3};1)$ .

a) Tính tích vô hướng của hai vectơ trên.

b) Tìm góc giữa của hai vectơ trên.

Hướng dẫn giải

a) Ta có: $\overrightarrow{u}$. $\overrightarrow{v}$ = 0.$\sqrt{3}$ + (–5).1= –5;

Vậy $\overrightarrow{u}$. $\overrightarrow{v}$ = –5.

b) Ta có $|\overrightarrow{u|}=\sqrt{0^2+{(-5)}^2}=5$; $\left|\overrightarrow{v}\right|=\sqrt{{\left(\sqrt{3}\right)}^2+1^2}=2$

Suy ra : cos($\overrightarrow{u}$, $\overrightarrow{v}$) = $\frac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\frac{-5}{5.2}=\frac{-5}{10}=\frac{-1}{2}$.

Suy ra ($\overrightarrow{u}$, $\overrightarrow{v}$) = 120°.

Vậy ($\overrightarrow{u}$, $\overrightarrow{v}$) = 120°.

• Tính chất của tích vô hướng :

Với ba vectơ $\overrightarrow{u}$, $\overrightarrow{v}$, $\overrightarrow{\text{w}}$ bất kì và mọi số thực k, ta có :

+) $\overrightarrow{u}$. $\overrightarrow{v}$ = $\overrightarrow{v}$. $\overrightarrow{u}$ (tính chất giao hoán);

+) $\overrightarrow{u}$. ($\overrightarrow{v}$ + $\overrightarrow{\text{w}}$) = $\overrightarrow{u}$. $\overrightarrow{v}$ + $\overrightarrow{u}$. $\overrightarrow{\text{w}}$ (tính chất phân phối đối với phép cộng) ;

+) (k $\overrightarrow{u}$). $\overrightarrow{v}$ = k ($\overrightarrow{u}$. $\overrightarrow{v}$) = $\overrightarrow{u}$.( k$\overrightarrow{v}$).

Chú ý: Từ tính trên, ta có thể chứng minh được :

$\overrightarrow{u}$. ($\overrightarrow{v}$ – $\overrightarrow{\text{w}}$)= $\overrightarrow{u}$. $\overrightarrow{v}$ – $\overrightarrow{u}$. $\overrightarrow{\text{w}}$ (tính chất phân phối đối với phép trừ) ;

($\overrightarrow{u}$ + $\overrightarrow{v}$)2 = ${\overrightarrow{u}}^2$ + 2$\overrightarrow{u}$. $\overrightarrow{v}$ + ${\overrightarrow{v}}^2$; ($\overrightarrow{u}$ – $\overrightarrow{v}$)2 = ${\overrightarrow{u}}^2$ –2$\overrightarrow{u}$.$\overrightarrow{v}$ + ${\overrightarrow{v}}^2$;

($\overrightarrow{u}$ + $\overrightarrow{v}$).($\overrightarrow{u}$ – $\overrightarrow{v}$) = ${\overrightarrow{u}}^2$ – ${\overrightarrow{v}}^2$.

Ví dụ: Cho tam giác ABC. Chứng minh rằng với điểm M tùy ý ta có:

$\overrightarrow{MA}.\overrightarrow{BC}+\overrightarrow{MB}.\overrightarrow{CA}+\overrightarrow{MC}.\overrightarrow{AB}=0$.

Hướng dẫn giải

Ta có $\overrightarrow{MA}.\overrightarrow{BC}=\overrightarrow{MA}.(\overrightarrow{MC}-\overrightarrow{MB})=\overrightarrow{MA}.\overrightarrow{MC}-\overrightarrow{MA}.\overrightarrow{MB};$(1)

$\overrightarrow{MB}.\overrightarrow{CA}=\overrightarrow{MB}.(\overrightarrow{MA}-\overrightarrow{MC})=\overrightarrow{MB}.\overrightarrow{MA}-\overrightarrow{MB}.\overrightarrow{MC};$ (2)

$\overrightarrow{MC}.\overrightarrow{AB}=\overrightarrow{MC}.(\overrightarrow{MB}-\overrightarrow{MA})=\overrightarrow{MC}.\overrightarrow{MB}-\overrightarrow{MC}.\overrightarrow{MA}$. (3)

Cộng các kết quả từ (1), (2), (3), ta được: $\overrightarrow{MA}.\overrightarrow{BC}+\overrightarrow{MB}.\overrightarrow{CA}+\overrightarrow{MC}.\overrightarrow{AB}=0$

Vậy $\overrightarrow{MA}.\overrightarrow{BC}+\overrightarrow{MB}.\overrightarrow{CA}+\overrightarrow{MC}.\overrightarrow{AB}=0$.

B.Bài tập tự luyện

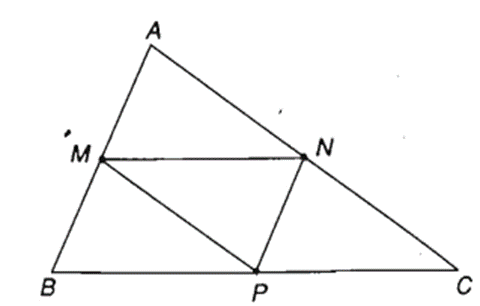
Bài 1: Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của AB, AC, BC.

a) Tìm hiệu $\overrightarrow{AM}-\overrightarrow{AN}$, $\overrightarrow{MN}-\overrightarrow{NC}$.

b) Phân tích $\overrightarrow{AM}$ theo hai vectơ $\overrightarrow{MN}$ và $\overrightarrow{MP}$.

Hướng dẫn giải

a) Ta có $\overrightarrow{AM}-\overrightarrow{AN}=\overrightarrow{NM}$ (theo quy tắc hiệu).

Do M, P lần lượt là trung điểm của AB và BC nên MP là đường trung bình của tam giác ABC.

Suy ra MP // AC và MP = $\frac{AC}{2}$.

Mặt khác N là trung điểm của AC, nên AN = $\frac{AC}{2}$.

Do đó MP // AN (vì hai đường thẳng AN và AC trùng nhau) và MP = AN.

Suy ra AMPN là hình bình hành.

Vì N là trung điểm của AC nên ta có $\overrightarrow{AN}=\overrightarrow{NC}$;

Do AMPN là hình bình hành nên $\overrightarrow{MP}=\overrightarrow{AN}$;

Do đó $\overrightarrow{MP}=\overrightarrow{NC}$.

Suy ra $\overrightarrow{MN}-\overrightarrow{NC}=\overrightarrow{MN}-\overrightarrow{MP}=\overrightarrow{PN}$.

Vậy $\overrightarrow{AM}-\overrightarrow{AN}=\overrightarrow{NM}$; $\overrightarrow{MN}-\overrightarrow{NC}=\overrightarrow{PN}$.

b) Do AMPN là hình bình hành nên ta có $\overrightarrow{AM}=\overrightarrow{NP}$

Suy ra $\overrightarrow{AM}=\overrightarrow{NP}=\overrightarrow{MP}-\overrightarrow{MN}$

Vậy $\overrightarrow{AM}=\overrightarrow{MP}-\overrightarrow{MN}$.

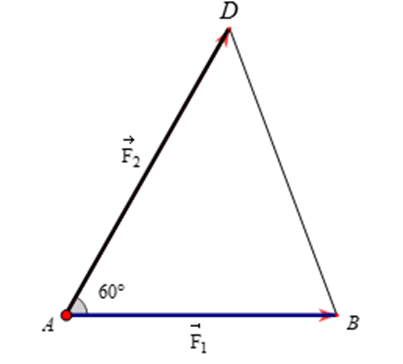
Bài 2: Hai lực $\overrightarrow{F_1}$ và $\overrightarrow{F_2}$ cùng tác động lên một vật, biết |$\overrightarrow{F_1}$| = 7N, |$\overrightarrow{F_2}$| = 8N. góc tạo bởi hai lực là 60°. Tính độ lớn của hợp lực $\overrightarrow{F_1}$ + $\overrightarrow{F_2}$.

Hướng dẫn giải:

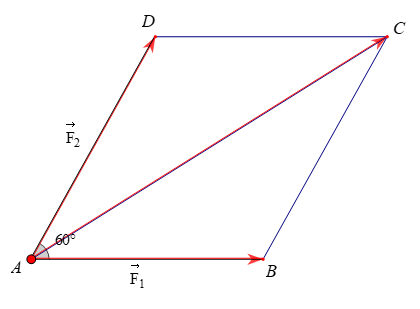
Đặt $\overrightarrow{AB}=\overrightarrow{F_1}$; $\overrightarrow{AD}=\overrightarrow{F_2}$. Ta vẽ hình bình hành ABCD.

Khi đó $\overrightarrow{F_1}$ + $\overrightarrow{F_2}$ = $\overrightarrow{AB}+\overrightarrow{AD}$ = $\overrightarrow{AC}$ (theo quy tắc hình bình hành).

Suy ra: |$\overrightarrow{F_1}$ + $\overrightarrow{F_2}$|=|$\overrightarrow{AC}$|

Do ABCD là hình bình hành nên AD // BC.

Suy ra $\widehat{DAB}+\widehat{CBA}=180°$ (hai góc trong cùng phía của hai đường thẳng song song).

⇒ $\widehat{CBA}=180°-\widehat{DAB}=180°-60°=120°$.

Mặt khác $\overrightarrow{AD}=\overrightarrow{BC}$ nên $\left|\overrightarrow{AD}\right|=\left|\overrightarrow{BC}\right|=\left|\overrightarrow{F_2}\right|=8$; $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{F_1}\right|=7$.

Áp dụng định lí côsin cho tam giác ABC ta có:

AC2 = AB2 + BC2 – 2.AB.BC.cosB

⇒ AC2 = 72 + 82 – 2.7.8.cos 1200 =169.

⇒ AC = $\sqrt{169}$ = 13

Suy ra |$\overrightarrow{F_1}$ + $\overrightarrow{F_2}$| = |$\overrightarrow{AC}$| = AC = 13

Vậy, |$\overrightarrow{F_1}$ + $\overrightarrow{F_2}$| = 13 (N).

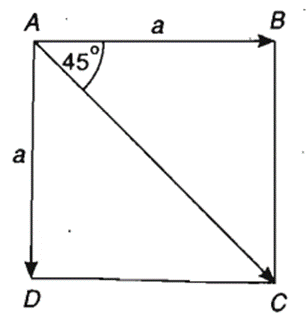
Bài 3: Cho hình vuông ABCD cạnh a. Tính tích $\overrightarrow{AB}.\overrightarrow{AD}$ và $\overrightarrow{AB}.\overrightarrow{AC}$.

Hướng dẫn giải

Do ABCD là hình vuông nên $(\overrightarrow{AB},\overrightarrow{AD})=\widehat{BAD}=90°$, $(\overrightarrow{AB},\overrightarrow{AC})=\widehat{BAC}=45°$.

Ta có: $\overrightarrow{AB}.\overrightarrow{AD}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AD}\right|.\cos (\overrightarrow{AB}.\overrightarrow{AD})=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AD}\right|.\cos 90°=0$.

Áp dụng định lí Pythagore cho tam giác ABC vuông tại B, ta có:

$A{C}^2=A{B}^2+B{C}^2=a^2+a^2=2a^2$

Suy ra AC = a$\sqrt{2}$.

Ta có: $\overrightarrow{AB}.\overrightarrow{AC}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|.\cos (\overrightarrow{AB},\overrightarrow{AC})=a.a\sqrt{2}.\cos 45°=a.a\sqrt{2}.\frac{\sqrt{2}}{2}=a^2$

Vậy $\overrightarrow{AB}.\overrightarrow{AD}$ = 0; $\overrightarrow{AB}.\overrightarrow{AC}$ = a2.

Bài 4: Cho $\overrightarrow{a}(3;-4)$ và $\overrightarrow{a}(3;-4)$.

a) Tính tích vô hướng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$.

b) Tính góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$.

Hướng dẫn giải

a) Ta có $\overrightarrow{a}$. $\overrightarrow{b}$ = 3 . 4 + (– 4) . 3 = 0.

Vậy $\overrightarrow{a}$. $\overrightarrow{b}$ = 0.

b) Ta có: cos($\overrightarrow{a}$, $\overrightarrow{b}$) = $\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{0}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=0$.

Suy ra ($\overrightarrow{a}$, $\overrightarrow{b}$) = 90°.

Vậy góc giữa hai vectơ $\overrightarrow{a}$ và là 90°.

Bài 5: Chứng minh $-(\overrightarrow{a}+\overrightarrow{b})=-\overrightarrow{a}+(-\overrightarrow{b})$.

Hướng dẫn giải

Giả sử $\overrightarrow{a}=\overrightarrow{AB},\overrightarrow{b}=\overrightarrow{BC}$ thì $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.

Ta có $-\overrightarrow{a}=-\overrightarrow{AB}=\overrightarrow{BA},-\overrightarrow{b}=-\overrightarrow{BC}=\overrightarrow{CB}$.

Do đó $-\overrightarrow{a}+(-\overrightarrow{b})=\overrightarrow{BA}+\overrightarrow{CB}=\overrightarrow{CB}+\overrightarrow{BA}=\overrightarrow{CA}=-\overrightarrow{AC}=-(\overrightarrow{a}+\overrightarrow{b})$.

Vậy $-(\overrightarrow{a}+\overrightarrow{b})=-\overrightarrow{a}+(-\overrightarrow{b})$.