Lý thuyết Đường tròn trong mặt phẳng tọa độ (Kết nối tri thức 2024) Toán 10

Lý thuyết Toán 10 Bài 21: Đường tròn trong mặt phẳng tọa độ

A. Lý thuyết Đường tròn trong mặt phẳng tọa độ

1. Phương trình đường tròn

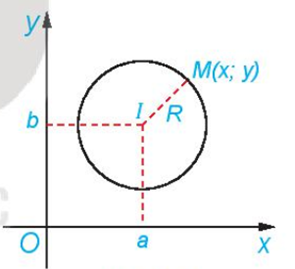
- Điểm M(x; y) thuộc đường tròn (C), tâm I(a; b), bán kính R khi và chỉ khi

(x – a)2 + (y – b)2 = R2 (1)

Ta gọi (1) là phương trình đường tròn (C).

Nhận xét:

- Phương trình (1) tương đương với: x2 + y2 – 2ax – 2by + (a2 + b2 – R2) = 0.

- Phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình của một đường tròn (C) khi và chỉ khi a2 + b2 – c > 0. Khi đó, (C) có tâm I(a; b) và bán kính $R=\sqrt{a^2+b^2-c}$

Ví dụ:

a) Viết phương trình đường tròn (C) có tâm I(2; –1) và bán kính R = 1.

b) Cho phương trình đường tròn x2 + y2 + 2x + 4y – 5 = 0. Hãy xác định tâm và bán kính của đường tròn này.

Hướng dẫn giải

a) Phương trình đường tròn (C) có tâm I(2; –1) và bán kính R = 1 là:

(x – 2)2 + (y + 1)2 = 1 .

b) Từ phương trình x2 + y2 + 2x + 4y – 5 = 0

⇔ x2 + y2 – 2.( –1).x – 2.( –2).y + (– 5) = 0

Khi đó a = –1 và b = –2, c = – 5.

Suy ra tâm của đường tròn này là I(–1; –2) và bán kính của đường tròn là:

$R=\sqrt{{(-1)}^2+{(-2)}^2-(-5)}=\sqrt{10}$

Vậy tâm của đường tròn này là: I(–1; –2) và bán kính R= $\sqrt{10}$.

2. Phương trình tiếp tuyến của đường tròn.

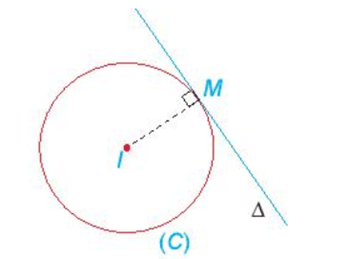
Cho điểm M(x0; y0) thuộc đường tròn (C): (x – a)2 + (y – b)2 = R2 (tâm I(a; b), bán kính R). Khi đó, tiếp tuyến ∆ của (C) tại M(x0; y0) có vectơ pháp tuyến $\overrightarrow{MI}=(a-x_0;b-y_0)$ và phương trình:

(a – x0)(x – x0) + (b – y0)(y – y0) = 0.

Ví dụ: Cho đường tròn (C) có phương trình (x – 1)2 + (y + 2)2 = 10 và điểm M(0; 1) thuộc đường tròn (C). Hãy viết phương trình tiếp tuyến của (C) tại điểm M.

Hướng dẫn giải

Từ phương trình đường tròn (C): (x – 1)2 + (y + 2)2 = 10 suy ra tâm của (C) là I(1; –2).

Tiếp tuyến của (C) tại M là đường thẳng đi qua M và vuông góc với MI.

Khi đó tiếp tuyến của (C) tại M(0; 1) có vectơ pháp tuyến $\overrightarrow{MI}=(1-0;-2-1)=(1;-3)$ , nên ta có phương trình:

1(x – 0) + (–2)(y – 1) = 0 ⇔ x – 2y + 2 = 0.

Vậy phương trình tiếp tuyến của (C) tại M(0; 1) là x – 2y + 2 = 0.

B. Bài tập Đường tròn trong mặt phẳng tọa độ

Bài 1: Cho phương trình là x2 + y2 + 6x + 8y + 7 = 0. Phương trình này có phải là phương trình đường tròn hay không? Nếu có, hãy tìm tâm và bán kính của đường tròn đó.

Hướng dẫn giải

Ta có : x2 + y2 + 6x + 8y + 7 = 0 ⇔ x2 + y2 –2.( –3)x –2.( –4)y + 7 = 0.

Suy ra a = –3 ; b = –4 ; c = 7.

Vì a2 + b2 – c = (–3)2 + (–4)2 – 7 = 18 > 0 nên x2 + y2 + 6x + 8y + 7 = 0 là phương trình của một đường tròn (C).

Đường tròn (C) có tâm I(–3; –4) và bán kính $R=\sqrt{a^2+b^2-c}=\sqrt{18}=3\sqrt{2}$.

Vậy, phương trình x2 + y2 + 6x + 8y + 7 = 0 là phương trình của một đường tròn (C) có tâm I(–3; –4) và bán kính R = $3\sqrt{2}$

Bài 2: Cho hai điểm A(3; –4 ); B(–3; 4).Viết phương trình đường tròn (C) nhận AB làm đường kính.

Hướng dẫn giải

Ta có $\overrightarrow{AB}=(-3-3;4-(-4\left)\right)=(-6;8)$ ⇒ AB = $\left(\overrightarrow{AB}\right)$ = $\sqrt{{(-6)}^2+8^2}=10$

Gọi M là trung điểm của AB.

Khi đó tọa độ của điểm M thỏa mãn: $\left(\begin{array}{c}{x}_M=\frac{x_A+x_B}{2}=\frac{3+(-3)}{2}=0\\ y_M=\frac{y_A+y_B}{2}=\frac{-4+4}{2}=0\end{array}\right)$ ⇒ M(0; 0).

Do đường tròn (C) có đường kính là AB nên điểm M chính là tâm của đường tròn và bán kính đường tròn $R=\frac{AB}{2}=\frac{10}{2}=5$

Phương trình đường tròn (C) là: (x – 0)2 + (y – 0)2 = 52 ⇔ x2 + y2 = 25.

Vậy đường tròn (C) có phương trình là x2 + y2 = 25.

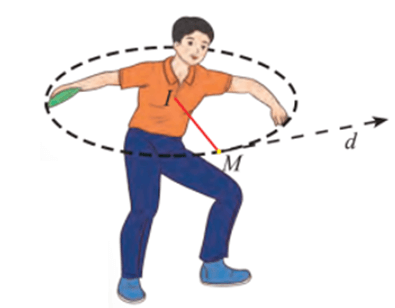
Bài 3: Một vận động viên ném đĩa vung đĩa theo một đường tròn (C) có phương trình là: x2 + y2 = $\frac{100}{81}$ .

Khi người đó vung đĩa đến vị trí điểm A( $\frac{6}{9}$; $\frac{8}{9}$ ) thì buông đĩa. Hãy viết phương trình tiếp tuyến của đường tròn (C).

Hướng dẫn giải

Từ phương trình đường tròn (C): x2 + y2 = $\frac{100}{81}$ suy ra tâm của (C) là O(0; 0).

Tiếp tuyến của (C) tại A( $\frac{6}{9}$; $\frac{8}{9}$ ) là đường thẳng đi qua A và vuông góc với OA.

Khi đó tiếp tuyến của (C) tại A($\frac{6}{9}$ ; $\frac{8}{9}$ ) có vectơ pháp tuyến , nên có phương trình:

$\frac{6}{9}$(x –$\frac{6}{9}$ ) +$\frac{8}{9}$ (y –$\frac{8}{9}$ ) = 0 ⇔ 3x + 4y – $\frac{50}{9}$ = 0.

Vậy phương trình tiếp tuyến của (C) tại A( $\frac{6}{9}$; $\frac{8}{9}$ ) là 3x + 4y – $\frac{50}{9}$ = 0.