Lý thuyết Vectơ trong mặt phẳng tọa độ (Kết nối tri thức 2024) Toán 10

Lý thuyết Toán lớp 10 Bài 10: Vectơ trong mặt phẳng tọa độ

A.Lý thuyếtVectơ trong mặt phẳng tọa độ

1. Tọa độ của vectơ

– Trục tọa độ (còn gọi là trục, hay trục số) là một đường thẳng mà trên đó đã xác định một điểm O và một vectơ $\overrightarrow{i}$ có độ dài bằng 1. Điểm O gọi là gốc tọa độ, vectơ $\overrightarrow{i}$ gọi là vectơ đơn vị của trục. Điểm M trên trục biểu diễn số x0 nếu $\overrightarrow{OM}=x_0\overrightarrow{i}$

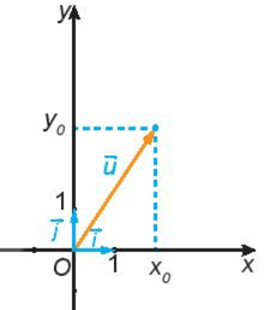
– Trên mặt phẳng với một đơn vị đo độ dài cho trước, xét hai trục Ox, Oy có chung gốc O và vuông góc với nhau. Kí hiệu vectơ đơn vị của trục Ox là $\overrightarrow{i}$, vectơ đơn vị của trục Oy là $\overrightarrow{j}$. Hệ gồm hai trục Ox, Oy như vậy được gọi là hệ trục tọa độ Oxy. Điểm O gọi là gốc tọa độ, trục Ox gọi là trục hoành, trục Oy gọi là trục tung. Mặt phẳng chứa hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy hay mặt phẳng Oxy.

– Mỗi vectơ $\overrightarrow{u}$ trên mặt phẳng Oxy, có duy nhất cặp số (x0; y0) sao cho $\overrightarrow{u}=x_0\overrightarrow{i}+y_0\overrightarrow{j}$.

Ta nói vectơ $\overrightarrow{u}$ có tọa độ (x0; y0) và viết $\overrightarrow{u}$ = (x0; y0) hay $\overrightarrow{u}$(x0; y0). Các số x0, y0 tương ứng được gọi là hoành độ, tung độ của $\overrightarrow{u}$.

– Hai vectơ bằng nhau khi và chỉ khi chúng có cùng tọa độ.

$\overrightarrow{u}(x;y)=\overrightarrow{v}(x\text{'};y\text{'})\iff \left(\begin{array}{c}x=x\text{'}\\ y=y\text{'}.\end{array}\right)$

Ví dụ : Trong mặt phẳng tọa độ Oxy, $\overrightarrow{u}$ = (2; –4). Hãy biểu diễn vectơ $\overrightarrow{u}$ qua vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$.

Hướng dẫn giải

Vì $\overrightarrow{u}$ = (2; –4) nên $\overrightarrow{u}=2\overrightarrow{i}+(-4)\overrightarrow{j}=2\overrightarrow{i}-4\overrightarrow{j}$

Vậy $\overrightarrow{u}=2\overrightarrow{i}-4\overrightarrow{j}$.

2. Biểu thức tọa độ của các phép toán vectơ

Cho hai vectơ $\overrightarrow{u}$ = (x; y) và $\overrightarrow{v}$ = (x’; y’). Khi đó :

$\overrightarrow{u}$ + $\overrightarrow{v}$ = (x + x’ ; y + y’) ;

$\overrightarrow{u}$ – $\overrightarrow{v}$ = (x – x’ ; y – y’) ;

k $\overrightarrow{u}$ = (kx ; ky) với k ∈ℝ.

Ví dụ : Cho $\overrightarrow{u}$ = (2; 3), = (–1; 2).

a) Tìm tọa độ của $\overrightarrow{u}$ + $\overrightarrow{v}$; $\overrightarrow{u}$ – $\overrightarrow{v}$.

b) Tìm tọa độ của vectơ 4$\overrightarrow{u}$.

Hướng dẫn giải

a) Ta có:

$\overrightarrow{u}$ + $\overrightarrow{v}$ = (2 + (–1); 3 + 2) = (1; 5)

$\overrightarrow{u}$ – $\overrightarrow{v}$ = (2 – (–1); 3 – 2) = (3; 1).

Vậy $\overrightarrow{u}$ + $\overrightarrow{v}$ = (1; 5) ; $\overrightarrow{u}$ – $\overrightarrow{v}$ = (3; 1).

b) 4$\overrightarrow{u}$ = (4.2 ; 4.3) = (8; 12)

Vậy 4$\overrightarrow{u}$ = (8; 12).

Nhận xét:

– Vectơ $\overrightarrow{v}$(x’; y’) cùng phương với vectơ $\overrightarrow{u}$(x; y) ≠ $\overrightarrow{0}$ khi và chỉ khai tồn tại số k sao cho x’ = kx, y’ = ky (hay là $\frac{x\text{'}}{x}=\frac{y\text{'}}{y}$ nếu xy ≠ 0).

– Nếu điểm M có tọa độ (x; y) thì vectơ $\overrightarrow{OM}$ có tọa độ (x; y) và độ dài $\left|\overrightarrow{OM}\right|=\sqrt{x^2+y^2}$.

– Với vectơ $\overrightarrow{u}$ = (x; y), ta lấy điểm M(x; y) thì $\overrightarrow{u}$ = $\overrightarrow{OM}$. Do đó $\left|\overrightarrow{u}\right|=\left|\overrightarrow{OM}\right|=\sqrt{x^2+y^2}$.

– Với hai điểm M(x; y) và N(x’ ; y’) thì và khoảng cách giữa hai điểm M, N là MN = $\left|\overrightarrow{MN}\right|=\sqrt{{(x\text{'}-x)}^2+{(y\text{'}-y)}^2}$.

Ví dụ: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(1; –2), B(3; 2), C(7; 4).

a) Tìm tọa độ của các vectơ $\overrightarrow{AB},\overrightarrow{BC}$.

b) So sánh các khoảng cách từ B tới A và C.

c) Ba điểm A, B, C có thẳng hàng không?

Hướng dẫn giải

a) Ta có $\overrightarrow{AB}=(3-1;2-(-2\left)\right)=(2;4)$;

$\overrightarrow{BC}=(7-3;4-2)=(4;2).$

b) Các khoảng cách từ B đến A và C lần lượt là:

AB = $\left|\overrightarrow{AB}\right|=\sqrt{2^2+4^2}=\sqrt{20}=2\sqrt{5}$;

BC = $\left|\overrightarrow{BC}\right|=\sqrt{4^2+2^2}=\sqrt{20}=2\sqrt{5}$.

Suy ra AB = BC = $2\sqrt{5}$.

Vậy khoảng cách từ B đến A bằng khoảng cách từ B đến C.

c) Hai vectơ $\overrightarrow{AB}=(2;4)$ và $\overrightarrow{BC}=(4;2)$ không cùng phương (vì $\frac{2}{4}\ne \frac{4}{2}$).

Do đó các điểm A, B, C không cùng nằm trên cùng một đường thẳng.

Vậy ba điểm A, B, C không thẳng hàng.

Chú ý:

- Trung điểm M của đoạn thẳng AB có tọa độ là $\left(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}\right)$.

- Trọng tâm G của tam giác ABC có tọa độ là $\left(\frac{x_A+x_B+x_C}{3};\frac{y_A+y_B+y_C}{3}\right)$.

B.Bài tập tự luyện

Bài 1: Trong mặt phẳng tọa độ Oxy cho các điểm A(1; –2) và B(2; 1).

a) Tính độ dài các đoạn thẳng OA, OB.

b) Tam giác OAB là tam giác gì? Vì sao?

Hướng dẫn giải

a) Ta có $\overrightarrow{OA}=(1;-2)\Rightarrow \left|\overrightarrow{OA}\right|=\sqrt{1^2+{(-2)}^2}=\sqrt{5}$.

Suy ra OA = $\left|\overrightarrow{OA}\right|=\sqrt{5}$

Ta có $\overrightarrow{OB}=(2;1)\Rightarrow \left|\overrightarrow{OB}\right|=\sqrt{2^2+1^2}=\sqrt{5}$.

Suy ra OB = $\left|\overrightarrow{OB}\right|=\sqrt{5}$

Vậy OA = $\sqrt{5}$; OB = $\sqrt{5}$.

b) Ta có: $\overrightarrow{AB}=\left(1;3\right)$ nên $AB=\left(\overrightarrow{AB}\right)=\sqrt{1^2+3^2}=\sqrt{10}$.

Xét tam giác OAB có OA = OB nên tam giác OAB là tam giác cân tại O.

Vậy tam giác OAB cân tại O.

Bài 2: Cho $\overrightarrow{u}=(3;-2)$ và $\overrightarrow{v}=(7;4)$. Tìm tọa độ của các vectơ $\overrightarrow{u}+\overrightarrow{v}$, $\overrightarrow{u}-\overrightarrow{v}$, $3\overrightarrow{u}-4\overrightarrow{v}$

Hướng dẫn giải

Ta có $\overrightarrow{u}+\overrightarrow{v}$ = (3 + 7; (–2) + 4) = (10; 2)

$\overrightarrow{u}-\overrightarrow{v}$ = (3 – 7 ; (–2) – 4) = (–4 ;–6)

$3\overrightarrow{u}=(3.3;3.(-2\left)\right)=(9;-6)$

$4\overrightarrow{v}=(4.7;\text{4.4) = (28;16)}$

Suy ra: $3\overrightarrow{u}-4\overrightarrow{v}=(9-28;(-6)-16)=(-19;-22)$.

Vậy: $\overrightarrow{u}+\overrightarrow{v}$ = (10 ; 2) ; $\overrightarrow{u}-\overrightarrow{v}$ =(4 ;– 6) ; $3\overrightarrow{u}-4\overrightarrow{v}=(-19;-22)$.

Bài 3: Cho hình bình hành ABCD có A(–1; 3), B(2; 4), C(0; 1). Tìm tọa độ đỉnh D.

Hướng dẫn giải

Giả sử D(x; y), khi đó $\overrightarrow{AD}=(x+1;y-3)$; $\overrightarrow{BC}=(0-2;1-4)=(-2;-3)$.

Vì ABCD là hình bình hành nên ta có: $\overrightarrow{AD}=\overrightarrow{BC}$. Do đó:

$\left(\begin{array}{c}x+1=-2\\ y-3=-3\end{array}\right)\iff \left(\begin{array}{c}x=-3\\ y=0\end{array}\right)$

Vậy tọa độ điểm D(–3 ; 0).