Lý thuyết Hàm số, đồ thị và ứng dụng (Kết nối tri thức 2024) Toán 10

Lý thuyết Toán 10 Chương 6: Hàm số, đồ thị và ứng dụng

A. Lý thuyết Chương 6: Hàm số, đồ thị và ứng dụng

1. Khái niệm hàm số

Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập hợp số thực ℝ thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D gọi là tập xác định của hàm số.

Tập tất cả các giá trị y nhận được, gọi là tập giá trị của hàm số.

Ví dụ : Viết hàm số mô tả sự phụ thuộc giữa diện tích S và bán kính r của hình tròn. Tìm tập xác định của hàm số đó.

Hướng dẫn giải

Diện tích S của hình tròn phụ thuộc vào bán kính r theo công thức S = π.r2, trong đó r là biến số, S = S(r) là hàm số của r.

Vì r là bán kính của hình tròn nên r > 0.

Do đó tập xác định của hàm số S = π.r2 là D = (0 ; +∞).

Vậy hàm số mô tả sự phụ thuộc giữa diện tích và bán kính của hình tròn là: S = S(r) = π.r2 và tập xác định của hàm số đó là: D = (0 ; +∞).

Chú ý : Khi cho hàm số bằng công thức y = f(x) mà không chỉ rõ tập xác định của nó thì ta quy ước tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

Ví dụ :

a) Tìm tập xác định của hàm y = $\sqrt{x+3}$

b) Tìm tập xác định của hàm y = $\frac{2x+4}{-x-1}$

Hướng dẫn giải

a) Biểu thức $\sqrt{x+3}$ có nghĩa khi x + 3 ≥ 0, tức là x ≥ – 3.

Vậy tập xác định của hàm số y = $\sqrt{x+3}$ là D = [– 3 ; +∞).

b) Biểu thức $\frac{2x+4}{-x-1}$ có nghĩa khi –x – 1 ≠ 0, tức là x ≠ –1.

Vậy tập xác định của hàm số y = $\frac{2x+4}{-x-1}$ là D = ℝ\{–1}.

Nhận xét : Một hàm số có thể cho bằng bảng, bằng biểu đồ, bằng công thức hoặc mô tả bằng lời.

Ví dụ :

a) Hàm số cho bởi công thức như hàm số y = f(x) = 2x + 7 ;

b) Nhiệt độ T(°C) tại các thời điểm t (giờ) trong cùng một ngày được cho bởi bảng sau :

Nhiệt độ T(°C) phụ thuộc vào sự thay đổi của thời gian t (giờ) và mỗi giờ chỉ tương ứng với đúng một giá trị nhiệt độ nên tương ứng đó xác định một hàm số.

Vậy bảng trên biểu thị một hàm số.

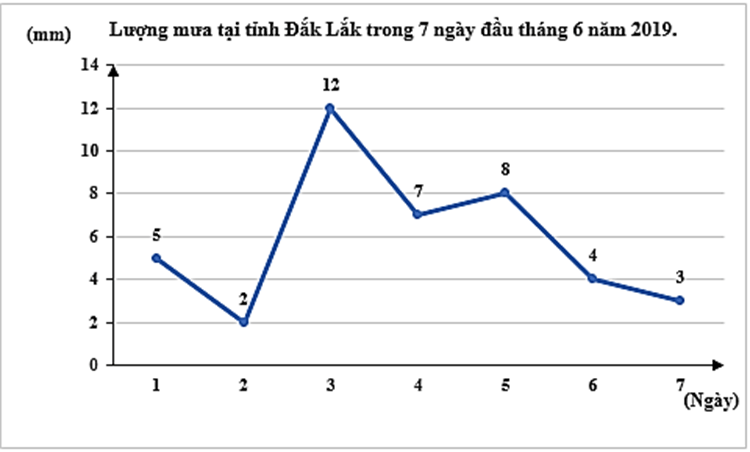
c) Cho biểu đồ sau:

Quan sát biểu đồ trên ta thấy ứng với mỗi ngày chỉ có đúng một giá trị lượng mưa nên tương ứng đó xác định một hàm số.

Vậy biểu đồ trên biểu thị một hàm số.

2. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x ; f(x)) trên mặt phẳng tọa độ với mọi x thuộc D.

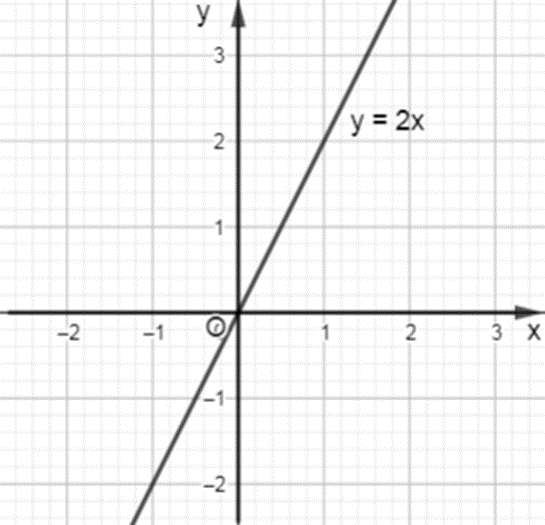
Ví dụ: Tìm tập xác định và vẽ đồ thị của hàm số y = 2x trên mặt phẳng tọa độ.

Hướng dẫn giải

Vì 2x xác định với mọi x ∈ℝ nên tập xác định của hàm số y = 2x là D = ℝ.

Đồ thị của hàm số y = 2x là một đường thẳng đi qua gốc tọa độ như trong hình sau :

3. Sự đồng biến, nghịch biến của hàm số

- Hàm số y = f(x) được gọi là đồng biến (tăng) trên khoảng (a ; b), nếu

∀ x1, x2 ∈ (a ; b), x1 < x2 ⇒ f(x1) < f(x2).

- Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a ; b), nếu

∀ x1, x2 ∈ (a ; b), x1 < x2 ⇒ f(x1) > f(x2).

Chú ý:

- Đồ thị của một hàm số đồng biến trên khoảng (a; b) là đường “đi lên” từ trái sang phải;

- Đồ thị của một hàm số nghịch biến trên khoảng (a; b) là đường “đi xuống” từ trái sang phải.

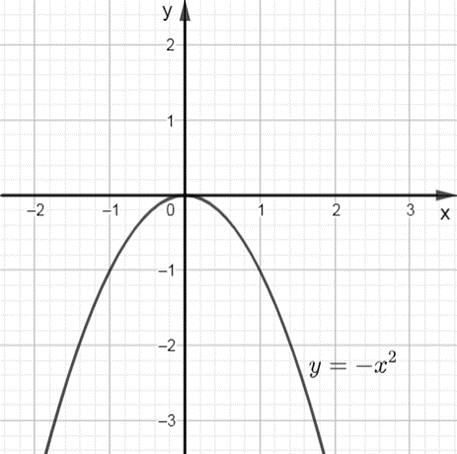
Ví dụ: Cho hàm số y = –x2 có đồ thị hàm số như hình sau:

Hàm số y = –x2 đồng biến hay nghịch biến trên mỗi khoảng (–∞; 0) và (0; +∞).

Hướng dẫn giải

Quan sát đồ thị hàm số y = –x2 ta thấy trên khoảng (–∞; 0), đồ thị đi lên từ trái sang phải. Do đó hàm số đồng biến trên khoảng (–∞; 0).

Ta thấy trên khoảng (0; +∞), đồ thị đi xuống từ trái sang phải. Do đó hàm số nghịch biến trên khoảng (0; +∞).

Vậy hàm số y = –x2 đồng biến trên khoảng (–∞; 0) và nghịch biến trên khoảng (0; +∞).

4. Khái niệm hàm số bậc hai

Hàm số bậc hai là hàm số cho bởi công thức y = ax2 + bx + c, trong đó x là biến số, a, b, c là các hằng số và a ≠ 0.

Tập xác định của hàm số bậc hai là ℝ.

Nhận xét : Hàm số y = ax2 (a ≠ 0) đã học ở lớp 9 là một trường hợp đặc biệt của hàm số bậc hai với b = c = 0.

Ví dụ:

a) Hàm số y = 2x2 + x – 1 là hàm số bậc hai với a = 2, b = 1, c = –1.

b) Hàm số y = – x2 cũng là hàm số bậc hai với a = –1 và b = c = 0.

5. Đồ thị của hàm số bậc hai

- Đồ thị của hàm số bậc hai là một parabol.

- Đồ thị hàm số y = ax2 + bx + c (a ≠ 0) là một đường parabol có đỉnh là điểm $I\left(-\frac{b}{2a};-\frac{\Delta }{4a}\right)$, có trục đối xứng là đường thẳng $x=-\frac{b}{2a}$. Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0.

- Để vẽ đường parabol y = ax2 + bx + c ta tiến hành theo các bước sau :

1. Xác định tọa độ đỉnh $I\left(-\frac{b}{2a};-\frac{\Delta }{4a}\right)$ ;

2. Vẽ trục đối xứng $x=-\frac{b}{2a}$;

3. Xác định tọa độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol ;

4. Vẽ parabol.

Nhận xét : Từ đồ thị hàm số y = ax2 + bx + c (a ≠ 0), ta suy ra tính chất của hàm số y = ax2 + bx + c (a ≠ 0):

Với a > 0	Với a < 0
Hàm số nghịch biến trên khoảng $\left(-\infty ;-\frac{b}{2a}\right)$ ; Hàm số đồng biến trên khoảng $\left(-\frac{b}{2a};+\infty \right)$ ; $-\frac{\Delta }{4a}$ là giá trị nhỏ nhất của hàm số.	Hàm số đồng biến trên khoảng $\left(-\infty ;-\frac{b}{2a}\right)$; Hàm số nghịch biến trên khoảng $\left(-\frac{b}{2a};+\infty \right)$ ; $-\frac{\Delta }{4a}$ là giá trị lớn nhất của hàm số.

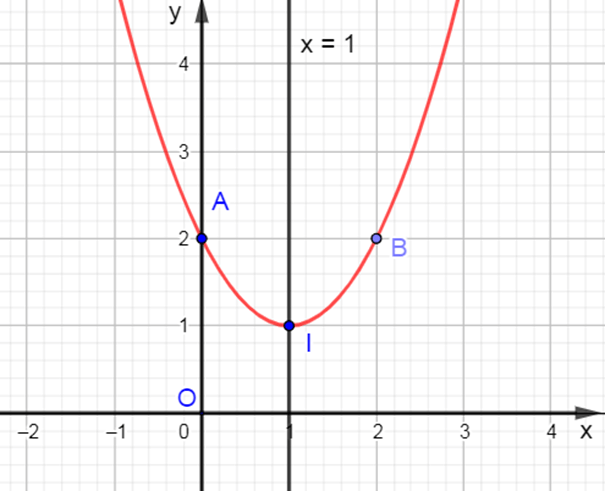
Ví dụ : Hãy vẽ parabol y = x2 – 2x + 2 và chỉ ra khoảng đồng biến, nghịch biến và giá trị nhỏ nhất của hàm số đó.

Hướng dẫn giải

Hàm số y = x2 – 2x + 2 có hệ số a = 1; b = – 2 ; c = 2.

Ta có : ∆ = (– 2)2 – 4.1.2 = –4.

Vì a = 1 > 0 nên parabol quay bề lõm lên trên.

Khi đó đỉnh $I=\left(-\frac{-2}{2.1};-\frac{-4}{4.1}\right)$ = (1 ; 1); trục đối xứng $x=-\frac{b}{2a}=-\frac{-2}{2.1}=1$.

Giao của đồ thị với trục Oy là A(0 ; 2).

Vì ∆ = – 4 < 0 nên phương trình x2 – 2x + 2 = 0 vô nghiệm, do đó đồ thị không giao với trục Ox.

Ta lấy điểm B(2; 2) đối xứng với A(0; 2) qua đường thẳng x = 1.

Ta có parabol y = x2 – 2x + 2 như hình vẽ sau :

b) Vì a = 1 > 0 nên ta có :

Hàm số y = x2 – 2x + 2 nghịch biến trên khoảng (–∞; 1);

Hàm số y = x2 – 2x + 2 đồng biến trên khoảng (1; +∞);

Giá trị nhỏ nhất của hàm số là y = 1, khi x = 1.

6. Dấu của tam thức bậc hai

Tam thức bậc hai (đối với x) là biểu thức có dạng ax2 + bx + c, trong đó a, b, c là những số thực cho trước (với a ≠ 0), được gọi là các hệ số của tam thức bậc hai.

Chú ý : Nghiệm của phương trình bậc hai ax2 + bx + c = 0 cũng là nghiệm của tam thức bậc hai ax2 + bx + c.

Ví dụ : Trong các biểu thức sau, biểu thức nào là tam thức bậc hai và tìm nghiệm của tam thức bậc hai đó.

a) A = x2 + 6x + 10;

b) B = 2x3 + x;

c) C = $\sqrt{x}$ + 2x + 1.

Hướng dẫn giải

a) Biểu thức A = x2 + 6x + 10 có dạng tam thức bậc hai với a = 1; b = 6 ; c = 10.

Nghiệm của tam thức bậc hai x2 + 6x + 10 cũng chính là nghiệm của phương trình x2 + 6x + 10 = 0.

Xét phương trình x2 + 6x + 10 = 0 có ∆ = 62 – 4.1.10 = –4 < 0

Suy ra phương trình x2 + 6x + 10 = 0 vô nghiệm.

Vậy tam thức bậc hai x2 + 6x + 10 vô nghiệm.

b) Đa thức 2x3 + x có bậc là 3 nên biểu thức B = 2x3 + x không phải là tam thức bậc hai.

c) Biểu thức C = $\sqrt{x}$ + 2x + 1 không có dạng ax2 + bx + c (a ≠ 0), do đó nó không phải là tam thức bậc hai.

Vậy biểu thức A = x2 + 6x + 10 là tam thức bậc hai và tam thức này vô nghiệm.

Định lí về dấu của tam thức bậc hai

Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0).

+ Nếu ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ℝ.

+ Nếu ∆ = 0 thì f(x) cùng dấu với hệ số a với mọi $x\ne -\frac{b}{2a}$ và $f\left(-\frac{b}{2a}\right)=0$

+ Nếu ∆ > 0 thì tam thức f(x) có hai nghiệm phân biệt x1 và x2 (x1 < x2). Khi đó, f(x) cùng dấu với hệ số a với mọi x ∈ (–∞; x1) ∪ (x2; +∞); f(x) trái dấu với hệ số a với mọi x ∈ (x1; x2).

Tức là, khi ∆ > 0, dấu của f(x) và a là: “Trong trái, ngoài cùng”

Chú ý: Trong định lí về dấu của tam thức bậc hai có thể thay ∆ bởi ∆’.

Ví dụ: Xét dấu của tam thức bậc hai sau:

a) f(x) = –2x2 + x – 2;

b) f(x) = – 4x2 – 12x – 9.

c) f(x) = 2x2 – x – 15.

Hướng dẫn giải

a) Xét f(x) = – 2x2 + x – 2 có ∆ = 12 – 4. (–2).(–2) = –15 < 0 .

Mặt khác a = –2 < 0 nên f(x) luôn cùng dấu với hệ số a = –2 < 0.

Vậy f(x) luôn âm với mọi x ∈ℝ.

b) Xét f(x) = – 4x2 – 12x – 9.

Ta có ∆ = (–12)2 – 4. (–4). (–9) = 0

Mặt khác a = –4 < 0 nên f(x) cùng dấu với a = –4 < 0 với mọi x ≠ $-\frac{3}{2}$ và f( $-\frac{3}{2}$) = 0.

Vậy f(x) âm với mọi x ≠ $-\frac{3}{2}$ và f( $-\frac{3}{2}$) = 0.

c) Xét f(x) = 2x2 – x – 15.

Ta có ∆ = (–1)2 – 4. 2 (–15) = 121 > 0.

Khi đó f(x) có hai nghiệm phân biệt $x_1=\frac{1+\sqrt{121}}{2.2}=3$ và $x_2=\frac{1-\sqrt{121}}{2.2}=-\frac{5}{2}$ .

Mặt khác a = 2 > 0 nên ta có bảng xét dấu sau :

Vậy f(x) dương trong khoảng $\left(-\infty ;-\frac{5}{2}\right)\cup \left(3;+\infty \right)$ và âm trong khoảng .

7. Bất phương trình bậc hai

- Bất phương trình bậc hai ẩn x là bất phương trình có dạng ax2 + bx + c > 0 (hoặc ax2 + bx + c ≥ 0, ax2 + bx + c < 0, ax2 + bx + c ≤ 0), trong đó a, b, c là những số thực đã cho và a ≠ 0.

- Số thực x0 gọi là một nghiệm của bất phương trình bậc hai ax2 + bx + c > 0, nếu ax02 + bx0 + c > 0. Tập hợp gồm tất cả các nghiệm của bất phương trình bậc hai ax2 + bx + c > 0 gọi là tập nghiệm của bất phương trình này.

- Giải một bất phương trình bậc hai là tìm tập nghiệm của nó.

Nhận xét: Để giải bất phương trình bậc hai ax2 + bx + c > 0 (hoặc ax2 + bx + c ≥ 0, ax2 + bx + c < 0, ax2 + bx + c ≤ 0) ta cần xét dấu tam ax2 + bx + c, từ đó suy ra tập nghiệm.

Ví dụ: Giải bất phương trình sau: 2x2 – 5x + 3 < 0;

Hướng dẫn giải

Đặt f(x) = 2x2 – 5x + 3

Ta có ∆ = (–5)2 – 4.2.3 = 1 > 0

Do đó f(x) = 2x2 – 5x + 3 có hai nghiệm phân biệt là :

$x_1=\frac{5+\sqrt{1}}{2.2}=\frac{3}{2}$ và $x_2=\frac{5-\sqrt{1}}{2.2}=1$ .

Mặt khác a = 2 > 0 nên ta có bảng xét dấu sau :

Từ bảng xét dấu trên ta thấy f(x) = 2x2 – 5x + 3 < 0 khi x ∈ $\left(1;\frac{3}{2}\right)$ .

Vậy tập nghiệm của bất phương trình 2x2 – 5x + 3 < 0 là $\left(1;\frac{3}{2}\right)$ .

8. Phương trình dạng $\sqrt{a{x}^2+bx+c}=\sqrt{d{x}^2+ex+f}$

Để giải phương trình $\sqrt{a{x}^2+bx+c}=\sqrt{d{x}^2+ex+f}$ ta thực hiện như sau:

- Bình phương hai vế và giải phương trình nhận được;

- Thử lại các giá trị tìm được ở trên có thỏa mãn phương trình đã cho hay không và kết luận nghiệm.

Ví dụ: Giải phương trình $\sqrt{x^2-7x}=\sqrt{-x^2-8x+3}$

Hướng dẫn giải

Bình phương hai vế của phương trình $\sqrt{x^2-7x}=\sqrt{-x^2-8x+3}$ , ta được:

x2 – 7x = –x2 – 8x + 3

⇒ 2x2 + x – 3 = 0.

Giải phương trình 2x2 + x – 3 = 0 ta được x1 = 1 và x2 = $-\frac{3}{2}$ .

Thay lần lượt x1 = 1 và x2 = $-\frac{3}{2}$ vào ta thấy chỉ có giá trị x2 = $-\frac{3}{2}$ thỏa mãn.

Vậy phương trình có nghiệm là x = $-\frac{3}{2}$.

9. Phương trình dạng $\sqrt{a{x}^2+bx+c}=dx+e$ .

Để giải phương trình $\sqrt{a{x}^2+bx+c}=dx+e$ , ta thực hiện như sau:

- Bình phương hai vế và giải phương trình nhận được;

- Thử lại các giá trị tìm được ở trên có thỏa mãn phương trình đã cho hay không và kết luận nghiệm.

Ví dụ: Giải phương trình $\sqrt{4x^2+x-1}=-x+1$

Bình phương hai vế của phương trình , ta được:

4x2 + x – 1 = (–x + 1)2

⇒ 4x2 + x – 1 = x2 – 2x + 1

⇒ 3x2 + 3x – 2 = 0.

Giải phương trình 3x2 + 3x – 2 = 0 ta được $x_1=\frac{-3+\sqrt{33}}{6}$ và $x_2=\frac{-3-\sqrt{33}}{6}$

Thay lần lượt $x_1=\frac{-3+\sqrt{33}}{6}$ và $x_2=\frac{-3-\sqrt{33}}{6}$ vào $\sqrt{4x^2+x-1}=-x+1$ ta thấy cả hai giá trị $x_1=\frac{-3+\sqrt{33}}{6}$ và $x_2=\frac{-3-\sqrt{33}}{6}$ đều thỏa mãn.

Vậy phương trình có hai nghiệm là $x_1=\frac{-3+\sqrt{33}}{6}$ và $x_2=\frac{-3-\sqrt{33}}{6}$

B. Bài tập Chương 6: Hàm số, đồ thị và ứng dụng

Bài 1: Xác định parabol y = ax2 + bx + c, biết parabol đi qua điểm A(4 ; 0) và có đỉnh là I(5 ; 7).

Hướng dẫn giải

Đỉnh của parabol là I(5 ; 7) do đó $-\frac{b}{2a}=5$ và 7 = a.52 + b.5 + c ⇒ 25a + 5b + c = 7.

Điểm A(4 ; 0) thuộc parabol nên ta có 0 = a.42 + b.4 + c ⇔ 16a + 4b + c = 0.

Khi đó, ta có hệ phương trình sau : $\left(\begin{array}{c}-\frac{b}{2a}=5\\ 25a+5b+c=7\\ 16a+4b+c=0\end{array}\right)$

Giải hệ trên ta được $\left(\begin{array}{c}a=-7\\ b=70\\ c=-168\end{array}\right)$

Vậy parabol cần tìm là y = –7x2 + 70x – 168.

Bài 2: Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y là hàm số của x.

a) 2x + y = –4;

b) y = –x2;

c) x = y2 (với x > 0).

Hướng dẫn giải

a) Ta có 2x + y = –4 ⇔ y = –2x – 4

Ta thấy với mỗi giá trị của x thì chỉ xác định được tương ứng một giá trị của y theo công thức y = –2x – 4.

Do đó y = –2x – 4 là hàm số của x.

b) Ta có với mỗi giá trị của x thì xác định một giá trị của y theo công thức y = –x2.

Do đó y = –x2 là hàm số của x.

c) Từ x = y2 ⇔ y = $\sqrt{x}$ hoặc y = $-\sqrt{x}$ (với x > 0).

Do đó với một giá trị của x xác định hai giá trị của y.

Vậy x = y2 (với x > 0) không phải là hàm số của x.

Bài 3: Tìm tập xác định của hàm số sau :

a) y = $\sqrt{2x-3}$ + $\sqrt{3-x}$

b) y = $\frac{x}{-x^2+2x+3}$

c) y = $\frac{1}{2}$x + 5.

Hướng dẫn giải

a) Ta có $\sqrt{2x-3}$ xác định khi 2x – 3 ≥ 0 ⇔ x ≥ $\frac{3}{2}$

$\sqrt{3-x}$ xác định khi 3 – x ≥ 0 ⇔ x ≤ 3.

Khi đó $\sqrt{2x-3}$ + $\sqrt{3-x}$ xác định khi x ≥ $\frac{3}{2}$ và x ≤ 3, tức là x ∈ [1,5 ; 3].

Vậy tập xác định của hàm số y = $\sqrt{2x-3}$ + $\sqrt{3-x}$ là D = [1,5 ; 3].

b) Ta có $\frac{x}{-x^2+2x+3}$ xác định khi –x2 + 2x + 3 ≠ 0 ⇔ x ≠ –1 và x ≠ 3.

Do đó y = $\frac{x}{-x^2+2x+3}$ xác định khi x ≠ –1 và x ≠ 3.

Vậy tập xác định của hàm số y = $\frac{x}{-x^2+2x+3}$ là D = ℝ \{–1 ; 3}.

c) Ta có $\frac{1}{2}$x + 5 xác định với mọi x∈ℝ.

Vậy hàm số y = $\frac{1}{2}$x + 5 có tập xác định D = ℝ.

Bài 4: Vẽ đồ thị hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng :

a) y = 2x – 1

b) y = –3x2.

Hướng dẫn giải

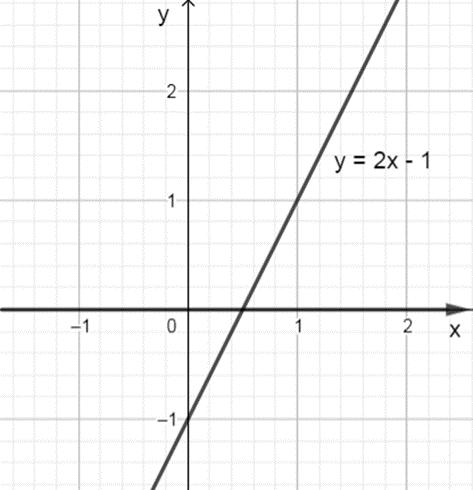
a) Hàm số y = 2x – 1 có tập xác định D = ℝ

Đồ thị hàm số y = 2x – 1 là đường thẳng đi qua hai điểm (0 ; – 1) và (; 0) dưới hình vẽ sau :

Quan sát hình vẽ ta thấy đồ thì hàm số đi lên từ trái sang phải nên hàm số y = 2x – 1 đồng biến trên toàn tập xác định.

Vậy hàm số y = 2x – 1 đồng biến trên ℝ.

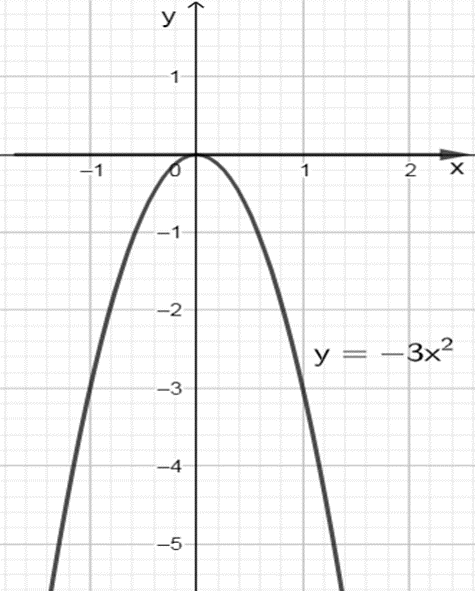
b) Hàm số y = –3x2 có tập xác định D = ℝ.

Đồ thị hàm số y = –3x2 là parabol trong hình vẽ sau :

Quan sát đồ thị hàm số y = –3x2 ta thấy trên khoảng (–∞; 0), đồ thị đi lên từ trái sang phải. Do đó hàm số đồng biến trên khoảng (–∞; 0).

Ta thấy trên khoảng (0; +∞), đồ thị đi xuống từ trái sang phải. Do đó hàm số nghịch biến trên khoảng (0; +∞).

Vậy hàm số y = –3x2 đồng biến trên khoảng (–∞; 0) và nghịch biến trên khoảng (0; +∞).

Bài 5: Hiện tại bạn Lan đã để dành được một số tiền là 500 nghìn đồng. Bạn Lan muốn mua một chiếc xe đạp có giá 2 triệu đồng, nên hằng ngày Lan đều tiết kiệm 20 nghìn đồng. Gọi y là số tiền Lan tiết kiệm được sau x ngày.

a) Viết công thức liên hệ giữa y và x.

b) Hỏi sau bao nhiêu lâu kể từ ngày bắt đầu tiết kiệm thì Lan đủ tiền mua chiếc xe đạp đó.

Hướng dẫn giải

a) Vì mỗi ngày Lan tiết kiệm 20 nghìn đồng nên x ngày Lan tiết kiệm được số tiền là 20x (nghìn đồng).

Mặt khác ban đầu Lan đã có 500 nghìn đồng nên sau x ngày số tiền Lan có là: 500 + 20x (nghìn đồng).

Tức là số tiền Lan tiết kiệm được sau x ngày là y = 500 + 20x (nghìn đồng).

Vậy ta có công thức liên hệ giữa y và x là hàm số : y = 500 + 20x.

b)

Khi Lan đủ tiền mua chiếc xe đạp đó, tức là Lan đã tiết kiệm đủ 2 triệu đồng.

Khi đó y = 2 triệu đồng = 2 000 (nghìn đồng).

Thay y = 2 000 vào hàm số y = 500 + 20x ta được :

2 000 = 500 + 20x

⇔ 20x = 1 500

⇔ x = 75

Suy ra sau 75 ngày thì Lan tiết kiệm được 2 triệu đồng.

Vậy sau 75 ngày kể từ ngày bắt đầu tiết kiệm thì Lan đủ tiền mua chiếc xe đạp đó.

Bài 6: Vẽ các parabol sau và xác định khoảng đồng biến, nghịch biến, giá trị lớn nhất, giá trị nhỏ nhất (nếu có).

a) y = x2 + 6x + 8

b) y = –x2 + 2x – 2

Hướng dẫn giải

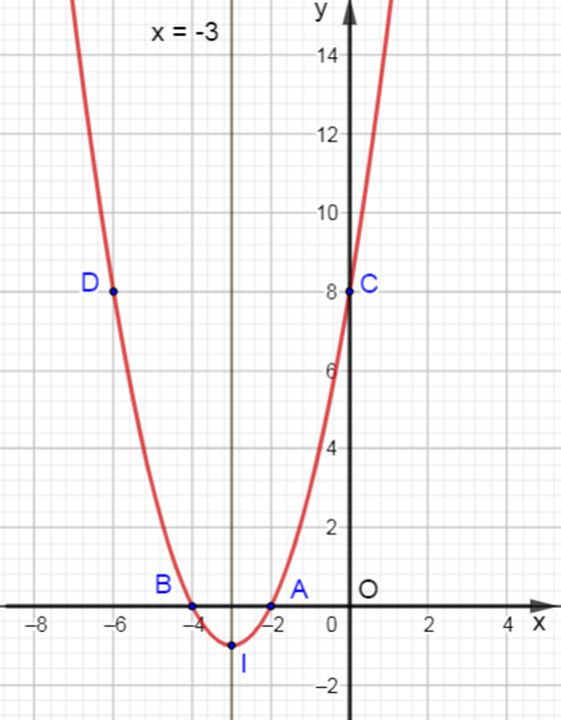
a) Hàm số y = x2 + 6x + 8 có hệ số a = 1; b = 6 ; c = 8

Ta có : ∆ = 62 – 4.1.8 = 4

Vì a = 1 > 0 nên parabol quay bề lõm lên trên.

Khi đó đỉnh I = $\left(-\frac{6}{2.1};-\frac{4}{4.1}\right)$ = (–3 ; –1); trục đối xứng $x=-\frac{b}{2a}=-\frac{6}{2.1}=-3$;

Giao của đồ thị với trục Ox là A(–2 ; 0) và B(–4 ; 0)

Giao của đồ thị với trục Oy là C(0 ; 8)

Ta lấy thêm điểm D(–6 ; 8) đối xứng với C(0 ; 8) qua đường thẳng x = –3 , điểm D cũng thuộc parabol.

Khi đó, ta có parabol y = x2 + 6x + 8 như hình vẽ sau :

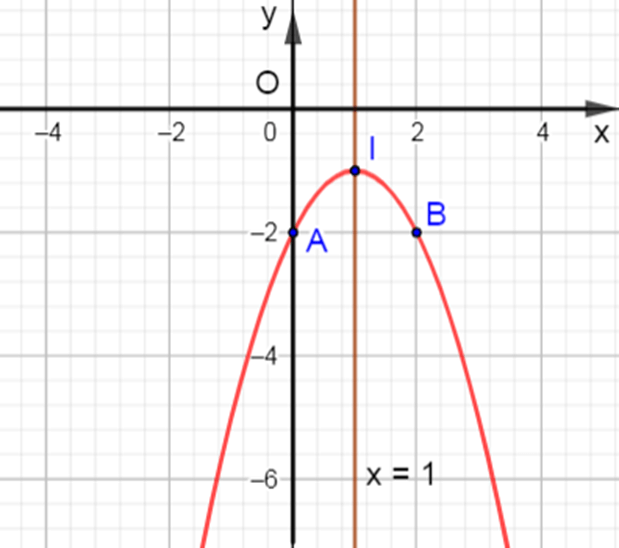
b) Hàm số y = –x2 + 2x – 2 có hệ số a = –1; b = 2 ; c = –2

Ta có : ∆ =22 – 4. (–1). (–2) = –4.

Vì a = –1 < 0 nên parabol quay bề lõm xuống dưới.

Khi đó đỉnh I =$\left(-\frac{2}{2.(-1)};-\frac{-4}{4.(-1)}\right)$ = (1 ; –1); trục đối xứng $x=-\frac{b}{2a}=-\frac{2}{2.(-1)}=1$.

Vì ∆ = –4 < 0 nên –x2 + 2x – 2 = 0 vô nghiệm, do đó đồ thị hàm số y = –x2 + 2x – 2 không cắt trục Ox.

Giao của đồ thị với trục Oy là A(0 ; –2)

Ta lấy thêm điểm B(2 ; –2) đối xứng với A(0 ; –2) qua đường thẳng x = 1, điểm B cũng thuộc parabol.

Khi đó, ta có parabol y = –x2 + 2x – 2 như hình vẽ sau :

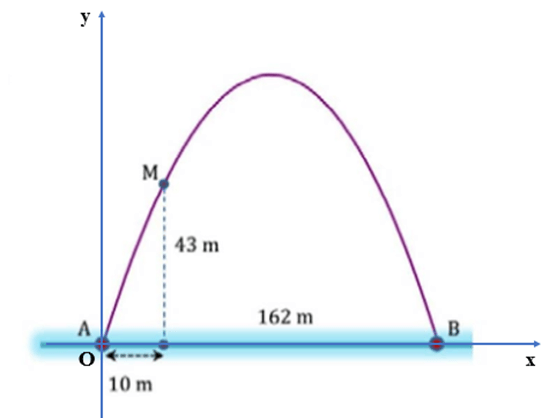
Bài 7: Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất, người ta thả một sợi dây chạm đất, vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch.

Hướng dẫn giải

Ta chọn hệ trục tọa độ như hình sau:

Gọi phương trình của parabol cần tìm là y = ax2 + bx + c (a ≠ 0).

Khi đó parabol đi qua ba điểm A(0 ; 0), B(162 ; 0) và M(10 ; 43).

Thay lần lượt tọa độ các điểm này vào phương trình parabol. Khi đó ta có hệ phương trình sau :

$\left(\begin{array}{c}a{.0}^2+b.0+c=0\\ a{.162}^2+b.162+c=0\\ a{.10}^2+b.10+c=43\end{array}\right)$

Giải hệ trên :

$\left(\begin{array}{c}a{.0}^2+b.0+c=0\\ a{.162}^2+b.162+c=0\\ a{.10}^2+b.10+c=43\end{array}\right)$⇔ $\left(\begin{array}{c}c=0\\ a{.162}^2+b.162=0\\ a{.10}^2+b.10=43\end{array}\right)\iff \left(\begin{array}{c}c=0\\ a=-\frac{43}{1520}\\ b=\frac{3483}{760}\end{array}\right)$

Suy ra parabol cần tìm là y = $-\frac{43}{1520}$x2 + $\frac{3483}{760}$x.

Ta có ∆ = ${\left(\frac{3483}{760}\right)}^2-4.\left(-\frac{43}{1520}\right).0={\left(\frac{3483}{760}\right)}^2$

Khi đó chiều cao của cổng là h = $-\frac{\Delta }{4a}$ = $-\frac{{\left(\frac{3483}{760}\right)}^2}{4.\left(-\frac{43}{1520}\right)}$ ≈ 185,6 (m).

Vậy chiều cao của cổng Arch khoảng 185,6 mét.

Bài 8: Xét dấu của các tam thức bậc hai sau:

a) f(x) = – 2x2 + 3x +5

b) g(x) = –x2 + 2x + 4

c) h(x) = 4x2 – 5x + 7

Hướng dẫn giải

a) Xét f(x) = –2x2 + 3x + 5 có ∆ = 32 – 4. (–2).5 = 49 > 0

Khi đó f(x) có hai nghiệm phân biệt $x_1=\frac{-3+\sqrt{49}}{2.(-2)}=-1$ và $x_2=\frac{-3-\sqrt{49}}{2.(-2)}=\frac{5}{2}$ .

Mặt khác a = –2 < 0 nênta có bảng xét dấu sau :

Vậy f(x) âm trong khoảng $\left(-\infty ;-1\right)\cup \left(\frac{5}{2};+\infty \right)$ và dương trong khoảng $\left(-1;\frac{5}{2}\right)$ .

b) Xét g(x) = –x2 + 2x –4 có ∆ = 22 – 4. (–1). (–4) = –12 < 0

Mặt khác a = –1 < 0 nên g(x) luôn cùng dấu với hệ số a = –1 < 0.

Vậy g(x) luôn âm với mọi x ∈ℝ.

c) Xét h(x) = 3x2 – 6x + 3 có ∆ = (–6)2 – 4.3.3 = 0.

Khi đó h(x) cùng dấu với hệ số a = 3 > 0 với mọi $x\ne -\frac{-6}{2.3}$ , tức là x ≠ 1 và h(1) = 0.

Vậy h(x) dương với mọi x ≠ 1 và h(1) = 0.

Bài 9: Giải các bất phương trình bậc hai:

a) 3x2 + 2x + 5 < 0

b) x2 + 12x + 36 > 0

c) 2x2 – x – 1 ≤ 0

Hướng dẫn giải

a) Đặt f(x) = 3x2 + 2x + 5

Ta có ∆ = 22 – 4.3.5 = –56< 0.

Khi đó f(x) luôn cùng dấu với a = 3 > 0 với mọi x ∈ℝ.

Tức là f(x) =3x2 + 2x + 5 > 0 với mọi x ∈ℝ.

Do đó bất phương trình 3x2 + 2x + 5 < 0 vô nghiệm.

b) Đặt g(x) = x2 + 12x + 36

Ta có ∆ = 122 – 4.1.36 = 0.

Khi đó g(x) luôn cùng dấu với a = 1 > 0 với mọi x ≠ –6 và g(–6) = 0.

Tức là g(x) = x2 + 12x + 36 > 0 với mọi x ≠ –6 và g(–6) = 0.

Do đó bất phương trình x2 + 12x + 36 > 0 khi x ≠ –6.

Vậy bất phương trình x2 + 12x + 36 > 0 có tập nghiệm là ℝ\{–6}.

c) Đặt h(x) = 2x2 – x – 1

Ta có ∆ = (–1)2 – 4.2.(–1) = 9> 0.

Khi đó h(x) có hai nghiệm phân biệt $x_1=\frac{-(-1)+\sqrt{9}}{2.2}=1$ và $x_2=\frac{-(-1)-\sqrt{9}}{2.2}=-\frac{1}{2}$ .

Mặt khác a = 2> 0 nênta có bảng xét dấu sau :

Từ bảng xét dấu ta thấy h(x) = 2x2 – x – 1 ≤ 0 khi x ∈ $\left(-\frac{1}{2};1\right)$.

Vậy bất phương trình 2x2 – x – 1 ≤ 0 có tập nghiệm là $\left(-\frac{1}{2};1\right)$

Bài 10: Tổng chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm được cho bởi biểu thức x2 + 20x + 3 100; giá bán của một sản phẩm là 150 nghìn đồng. Số sản phẩm sản xuất phải trong khoảng nào để đảm bảo không bị lỗ.

Hướng dẫn giải

Vì giá bán một sản phẩm là 150 nghìn đồng nên với x sản phẩm thì bán được 150x (nghìn đồng).

Do tổng chi phí để sản xuất ra x sản phầm là x2 + 20x + 3 100 nên lợi nhuận thu về từ x sản phẩm là:

150x – (x2 + 20x + 3 100) = – x2 + 130x – 3100.

Để không bị lỗ thì – x2 + 130x – 3 100 ≥ 0.

Đặt f(x) = – x2 + 130x – 3 100

Ta có: ∆ = 1302 – 4.(–1)( –3 100) = 4 500 > 0.

Khi đó f(x) có hai nghiệm phân biệt là $x_1=\frac{-130+\sqrt{4500}}{2.(-1)}=65-15\sqrt{5}\approx 31,5$ và $x_2=\frac{-130-\sqrt{4500}}{2.(-1)}=65+15\sqrt{5}\approx 98,5$.

Mặt khác a = –1 < 0 nên ta có bảng xét dấu sau:

Từ bảng xét dấu ta thấy f(x) = – x2 + 130x – 3 100 ≥ 0 khi x ∈ [31,5; 98,5].

Mặt khác, vì x là số sản phẩm nên để không bị lỗ thì x ∈ [32; 98].

Vậy để không bị lỗ thì số sản phẩm sản xuất phải từ 32 đến 98 sản phẩm.

Bài 11: Giải các phương trình sau :

a) $\sqrt{x^2+x+2}=\sqrt{x^2-x+1}$

b) $\sqrt{x^2-2x}=\sqrt{-3x^2-x+1}$

Hướng dẫn giải

a) Bình phương hai vế của phương trình $\sqrt{x^2+x+2}=\sqrt{x^2-x+1}$ , ta được:

x2 + x + 2 = x2 – x + 1

⇒ 2x = – 1

⇒ x = $-\frac{1}{2}$

Thay x = $-\frac{1}{2}$ vào phương trình $\sqrt{x^2+x+2}=\sqrt{x^2-x+1}$ ta thấy thỏa mãn.

Vậy phương trình $\sqrt{x^2+x+2}=\sqrt{x^2-x+1}$ có nghiệm là x = $-\frac{1}{2}$ .

b) Bình phương hai vế của phương trình $\sqrt{x^2-2x}=\sqrt{-3x^2-x+1}$ , ta được:

x2 – 2x = –3x2 – x + 1

⇒ 4x2 – x – 1 = 0

Phương trình 4x2 – x – 1 = 0 có hai nghiệm phân biệt là

$x_1=\frac{1+\sqrt{17}}{8}$ và $x_2=\frac{1-\sqrt{17}}{8}$ .

Thay lần lượt $x_1=\frac{1+\sqrt{17}}{8}$ và $x_2=\frac{1-\sqrt{17}}{8}$vào phương trình $\sqrt{x^2-2x}=\sqrt{-3x^2-x+1}$ ta thấy chỉ có $x_2=\frac{1-\sqrt{17}}{8}$ thỏa mãn.

Vậy phương trình $\sqrt{x^2-2x}=\sqrt{-3x^2-x+1}$ có nghiệm là $x=\frac{1-\sqrt{17}}{8}$

Bài 12: Giải các phương trình sau:

a) $\sqrt{4x^2+3x+1}=-2x+1$

b) .$\sqrt{-x^2+2x+33}-x=-x+5$

Hướng dẫn giải

a) Bình phương hai vế của phương trình $\sqrt{4x^2+3x+1}=-2x+1$ , ta được:

4x2 + 3x + 1 = 4x2 – 4x + 1

⇒ 7x = 0

⇒ x = 0

Thay x = 0 vào phương trình $\sqrt{4x^2+3x+1}=-2x+1$ ta thấy thỏa mãn.

Vậy phương trình $\sqrt{4x^2+3x+1}=-2x+1$ có nghiệm là x = 0.

b) Ta có $\sqrt{-x^2+2x+33}-x=-x+5\iff \sqrt{-x^2+2x+33}=5$

Bình phương hai vế của phương trình $\sqrt{-x^2+2x+33}=5$ , ta được:

– x2 + 2x + 33 = 25

⇒ – x2 + 2x + 8 = 0

Phương trình –x2 + 2x + 8 = 0 có hai nghiệm phân biệt x1 = –2 và x2 = 4.

Thay lần lượt x1 = –2 và x2 = 4 vào phương trình $\sqrt{-x^2+2x+33}=5$ta thấy cả hai giá trị đều thỏa mãn.

Vậy phương trình $\sqrt{-x^2+2x+33}-x=-x+5$ có hai nghiệm là x1 = –2 và x2 = 4.

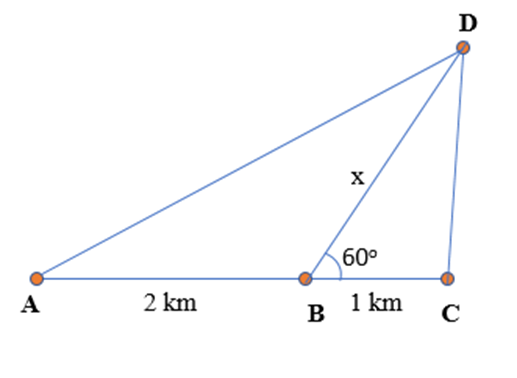
Bài 13: Nhà của An, Minh, Quân và Long lần lượt nằm trên các vị trí A, B, C, D như hình vẽ sau. Biết nhà An cách nhà Minh 2 km, nhà Minh cách nhà Quân 1 km. Biết khoảng cách từ nhà Long đến nhà Quân bằng $\frac{2}{3}$ khoảng cách từ nhà Long đến nhà An. Tính khoảng cách từ nhà Long đến nhà Minh.

Hướng dẫn giải

Gọi khoảng cách từ nhà Long đến nhà Minh là x (km), tức là DB = x km.

Nhà An cách nhà Minh 2 km nên AB = 2 km.

Nhà Minh cách nhà Quân 1 km nên BC = 1 km.

- Áp dụng định lí Côsin cho tam giác DBC ta có :

DC2 = DB2 + BC2 – 2.DB.BC.cos$\widehat{DBC}$ = x2 + 12 – 2.x.1.cos60° = x2 – x + 1

⇒ DC = $\sqrt{x^2-x+1}$ .

Suy ra khoảng cách từ nhà Long đến nhà Quân là $\sqrt{x^2-x+1}$ (km)

Ta có $\widehat{DBA}+\widehat{DBC}={180}^o$(hai góc kề bù)

Suy ra : $\widehat{DBA}={180}^o-\widehat{DBC}={180}^o-{60}^o={120}^o$.

- Áp dụng định lí Côsin cho tam giác DBA ta có :

AD2 = DB2 + AB2 – 2.DB.AB.cos$\widehat{DBA}$ = x2 + 22 – 2.x.2.cos120° = x2 + 2x + 4

⇒ AD = $\sqrt{x^2+2x+4}$.

Suy ra khoảng cách từ nhà Long đến nhà An là $\sqrt{x^2+2x+4}$ (km)

Do khoảng cách từ nhà Long đến nhà Quân bằng $\frac{2}{3}$ khoảng cách từ nhà Long đến nhà An nên ta có phương trình: $\sqrt{x^2-x+1}$ =$\frac{2}{3}$.$\sqrt{x^2+2x+4}$

Bình phương hai vế của phương trình $\sqrt{x^2-x+1}$=$\frac{2}{3}$ .$\sqrt{x^2+2x+4}$ ta được:

x2 – x + 1 = $\frac{4}{9}$(x2 + 2x + 4)

⇒ x2 – x + 1 = $\frac{4}{9}$x2 + $\frac{8}{9}$x + $\frac{16}{9}$

⇒ $\frac{5}{9}$x2 – $\frac{17}{9}$x – $\frac{7}{9}$ = 0.

Giải phương trình$\frac{5}{9}$ x2 –$\frac{17}{9}$ x – $\frac{7}{9}$ = 0 ta được x1 ≈ 3,8 và x2 ≈ – 0,4.

Vì x là khoảng cách từ nhà Long đến nhà Minh nên x > 0, do đó x2 ≈ – 0,4 không thỏa mãn.

Thay x1 ≈ 3,8 vào phương trình $\sqrt{x^2-x+1}$ = $\frac{2}{3}$. $\sqrt{x^2+2x+4}$ta thấy giá trị x1 ≈ 3,8 thỏa mãn.

Do đó phương trình $\sqrt{x^2-x+1}$ = $\frac{2}{3}$.$\sqrt{x^2+2x+4}$ có nghiệm là x ≈ 3,8.

Vậy khoảng cách từ nhà Long đến nhà Minh khoảng 3,8 km.