30 câu Trắc nghiệm Hình thoi và hình vuông (có đáp án 2024) – Toán 8 Kết nối tri thức
Bộ 30 câu hỏi trắc nghiệm Toán 8 (có đáp án) Bài 14: Hình thoi và hình vuông đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 8 Bài 14.
Trắc nghiệm Toán 8 Bài 14: Hình thoi và hình vuông
Câu 1. Khẳng định nào sau đây là sai?
A. Tứ giác có 4 cạnh bằng nhau là hình thoi.
B. Tứ giác có hai đường chéo vuông góc với nhau và bằng nhau là hình thoi.
C. Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
D. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
Đáp án đúng là: B
Câu A, C, D đúng theo dấu hiệu nhận biết hình thoi.
Câu B sai vì hai đường chéo không cắt nhau tại trung điểm mỗi đường.
Câu 2. Hình thoi không có tính chất nào dưới đây?
A. Hai đường chéo cắt nhau tại trung điểm mỗi đường.
B. Hai đường chéo là các đường phân giác của các góc của hình thoi.
C. Hai đường chéo vuông góc với nhau.
D. Hai đường chéo bằng nhau.
Đáp án đúng là: D
Hình thoi có tất cả các tính chất của hình bình hành
+ Các cạnh đối song song và bằng nhau, các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Ngoài ra còn có
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc của hình thoi.
Câu 3. Khẳng định nào sau đây là sai?
A. Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
B. Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
C. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
D. Tứ giác có bốn góc bằng nhau là hình thoi.
Đáp án đúng là: D
Vì theo dấu hiệu nhận biết hình thoi
⦁ Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
⦁ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
⦁ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
⦁ Hình chữ nhật là tứ giác có bốn góc bằng nhau nhưng bốn cạnh không bằng nhau nên không là hình thoi.
Câu 4. Các dấu hiệu nhận biết sau, dấu hiệu nào không đủ để kết luận một hình vuông?
A. Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
B. Hình thoi có một góc vuông là hình vuông.
C. Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
D. Hình thoi có hai đường chéo vuông góc là hình vuông.
Đáp án đúng là: D
Câu A, B, C là các câu đúng theo dấu hiệu nhận biết hình vuông.
Câu D sai vì hình thoi đã có sẵn hai đường chéo vuông góc, hình thoi cần có hai đường chéo bằng nhau thì mới là hình vuông.
Câu 5. Để chứng minh tứ giác ABCD là hình vuông, dấu hiệu nào sau đây là sai?
A. Tứ giác ABCD là hình thoi có hai đường chéo bằng nhau.
B. Tứ giác ABCD là hình thoi có một góc vuông.
C. Tứ giác ABCD là hình thoi có hai đường chéo vuông góc.
D. Tứ giác ABCD là hình chữ nhật có hai cạnh kề bằng nhau.
Đáp án đúng là: C
Tứ giác ABCD hình thoi có hai đường chéo AC, BD vuông góc với nhau nhưng chưa thể kết luận được ABCD là hình vuông.
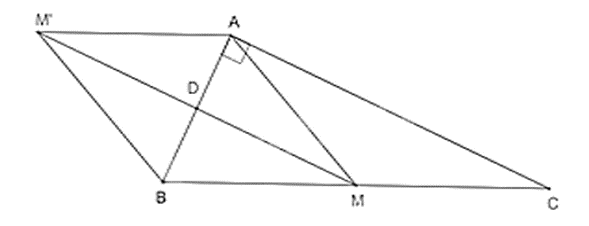
Câu 6. Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB và MD // AC, M′ là điểm đối xứng với M qua D. Tứ giác AMBM′ là hình gì?
A. Hình thoi.
B. Hình bình hành.
C. Hình chữ nhật.
D. Hình thang.
Đáp án đúng là: A
Vì M′ đối xứng M qua D nên DM = DM′ (1)
Ta có: MD // AC
Mặt khác ΔABC vuông ở A nên AB⊥AC.(2)
Từ (1) và (2) suy ra DM⊥AB⇒MM'.
Vì D là trung điểm của AB (gt) và D là trung điểm của MM′ nên tứ giác AMBM′ là hình bình hành.
Mặt khác nên AMBM′ là hình thoi. (Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.)
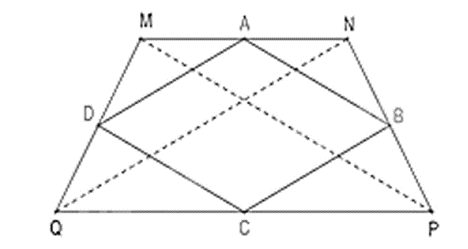
Câu 7. Cho hình thang cân MNPQ. Gọi A, B, C, D lần lượt là các điểm thuộc các cạnh MN, NP, PQ, QM và . Tứ giác ABCD là hình gì?
A. Hình chữ nhật.
B. Hình bình hành.
C. Hình thang cân.
D. Hình thoi.
Đáp án đúng là: D
Do MNPQ là hình thang cân nên MP = NQ. (hình thang cân có hai đường chéo bằng nhau). (1)
Xét các tam giác MNQ, PQN, MNP, QMP ta có:
(2)
Từ (1) và (2) suy ra AB = BC = CD = DA.
Do đó ABCD là hình thoi. (Tứ giác có bốn cạnh bằng nhau là hình thoi.)
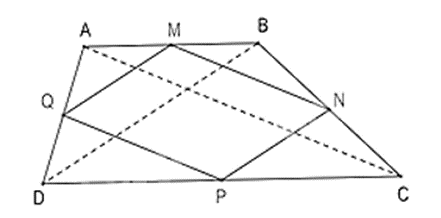
Câu 8. Cho hình thang ABCD. Gọi M, N, P, Q lần lượt là các điểm thuộc các cạnh AB, BC, CD, DA và ; ; . Hình thang ABCD có thêm điều kiện nào dưới đây thì MNPQ là hình thoi?
A. MP = QN
B. .
C. AB = AD.
D. AC = BD.
Đáp án đúng là: D
Xét tam giác ABC có: (1)
Xét tam giác ADC có: (2)
Từ (1) và (2) suy ra là hình bình hành.
Để hình bình hành MNPQ là hình thoi ta cần có MN = MQ.
Mà
Suy ra AC = BD.
Vậy để hình bình hành MNPQ là hình thoi thì AC = BD.
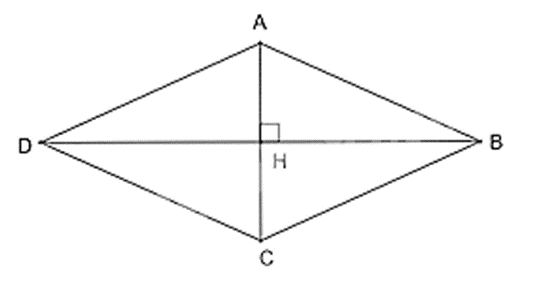
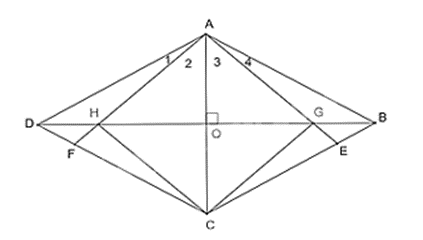
Câu 9. Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H thứ tự là giao điểm của AE, AF với đường chéo DB. Tứ giác AGCH là hình gì?
A. Hình thoi.
B. Hình chữ nhật.
C. Hình bình hành.
D. Hình thang.
Đáp án đúng là: A
Gọi O là giao điểm của AC và BD thì (do O là giao điểm của hai đường chéo của hình thoi)
Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD, ta được:
Từ đó suy ra (c.g.c).
Suy ra ( hai góc tương ứng).
Mà AC là phân giác của (1)
Xét tam giác AGH có AO là đường cao, đồng thời là đường phân giác nên tam giác AGH cân tại A.
Suy ra HO = OG (2)
Do ABCD là hình thoi nên AO = OC (tính chất đường chéo của hình thoi) (3)
Từ (1), (2), (3) suy ra: AHCG là hình thoi.
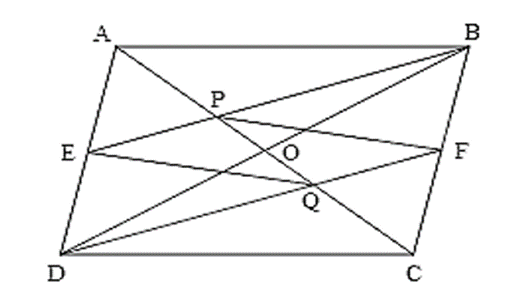
Câu 10. Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của AD, BC. Các đường BE, DF cắt AC tại P, Q . Tứ giác EPFQ là hình thoi nếu bằng
A. 45°.
B. 90°.
C. 60°.
D. 75°.
Đáp án đúng là: B
Gọi O là giao điểm của hai đường chéo AC và BD.
Vì ABCD là hình bình hành nên O là trung điểm của AC, BD và AD // CB, AD = BC
Xét tứ giác EDFB có ED // FB,
Nên EDFB là hình bình hành.
Suy ra: BE = DF, BE // DF.
Xét có P là giao điểm hai đường trung tuyến BE, AO nên P là trọng tâm
Xét có Q là giao điểm hai đường trung tuyến DF, CO nên Q là trọng tâm
Mà BE = DF (cmt) EP = QF.
Xét tứ giác EPFQ có EP = QF, EP // QF EPFQ là hình bình hành.
Để hình bình hành EPFQ là hình thoi thì .
Mà EF // CD (do hình bình hành ABCD có AB // CD, E là trung điểm AD, F là trung điểm BC ).
Nên hay
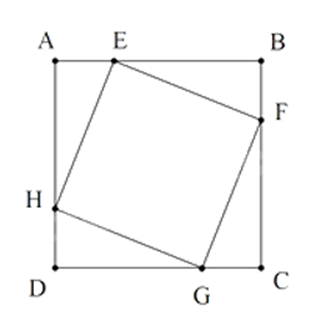
Câu 11. Cho hình vuông ABCD. Trên cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình bình hành.
B. Hình chữ nhật.
C. Hình thoi.
D. Hình vuông.
Đáp án đúng là: D
Ta có: AH = BE = CF = DG
Do đó: EH = FE = GF = HG (1)
Lại có:
Từ (1) và (2) suy ra tứ giác EFGH là hình vuông.
Hình thoi có một góc vuông là hình vuông.
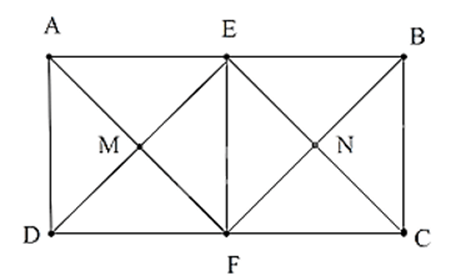
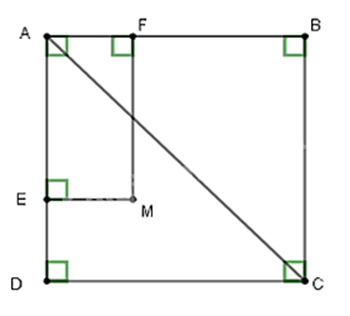
Câu 12. Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của AB, CD; EF // AD // BC. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Tứ giác EMFN là hình gì?
A. Hình bình hành.
B. Hình chữ nhật.
C. Hình thoi.
D. Hình vuông.
Đáp án cần chọn là: D
Vì EF // AD //BC
Và AE = FB = BC = CF = FD = DA
Lại có: AE // DF
Tứ giác ADFE là hình bình hành (dhnb)
Lại có: (do ABCD là hình chữ nhật)
Tứ giác ADFE là hình chữ nhật.
Mặt khác:
ADFE là hình vuông.
Chứng minh tương tự ta có BCFE là hình vuông
Do đó và là hai tam giác vuông cân tại M, N
Suy ra tứ giác EMFN là hình vuông.
Câu 13. Cho hình vuông ABCD. M là điểm nằm trong hình vuông. Gọi E, F lần lượt là hình chiếu của M trên cạnh AB và AD. Tứ giác AEMF là hình vuông khi
A. M trên đường chéo AC
B. M thuộc cạnh DC
C. M thuộc đường chéo BD
D. M tùy ý nằm trong hình vuông ABCD
Tứ giác AFME có: nên AEMF là hình chữ nhật
Để hình chữ nhật AEMF là hình vuông thì AM là phân giác của góc
Mà ta lại có: AC là phân giác (do ABCD là hình vuông)
Nên suy ra .
Đáp án đúng là: A
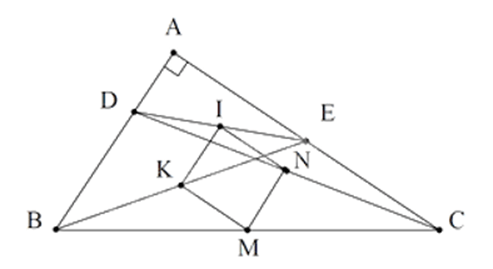
Câu 14. Tam giác ABC vuông tại A. Trên các cạnh AB, AC lấy các điểm D, E sao cho
BD = CE. Gọi I, K, M, N theo thứ tự là các điểm thuộc các cạnh DE, BE, CB, CD sao cho ; IK // BD, IN // CE. Tứ giác IKMN là hình gì?
A. Hình vuông.
B. Hình chữ nhật.
C. Hình bình hành.
D. Hình thoi.
Ta có:
Mà BD = CE nên IK = KM = MN = IN (1)
Lại có: IK // BD, IN //CE
Mặt khác:
(2)
Từ (1) và (2) suy ra IKMN là hình vuông.
Đáp án đúng là: A
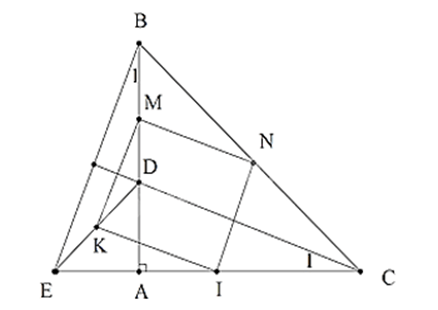
Câu 15. Cho tam giác ABC vuông cân tại A, điểm D thuộc cạnh AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AD. Gọi M, N, I, K theo thứ tự là các điểm thuộc các cạnh BD, BC, EC, ED sao cho . Tứ giác MNIK là hình gì?
A. Hình bình hành.
B. Hình chữ nhật.
C. Hình vuông.
D. Hình thoi.
Đáp án đúng là: C
Ta có: (c.g.c)
Suy ra: CD = BE
Lại có:
Mặt khác: phụ với nên phụ với
Do đó:
Theo đề bài ta có:
Từ đó suy ra MN = NI = KI = MK và
Do đó tứ giác MNIK là hình vuông.