30 câu Trắc nghiệm Phương trình bậc nhất một ẩn (có đáp án 2024) – Toán 8 Kết nối tri thức

Bộ 30 câu hỏi trắc nghiệm Toán 8 (có đáp án) Bài 25: Phương trình bậc nhất một ẩn đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 8 Bài 25.

1 174 lượt xem

Bài trước

Bài sau

Trắc nghiệm Toán 8 Bài 25: Phương trình bậc nhất một ẩn

Câu 1 : Ở một số quốc gia, người ta dùng cả hai đơn vị đo nhiệt độ là Fahrenheit (oF) và độ Celcius (oC), liên hệ với nhau bởi công thức $C = \frac{5}{9} (F - 32) .$ Khi ở 20 oC thì ứng với độ Fahrenheit là:

A
34 oF
B
38 oF
C
64 oF
D
68 oF

Đáp án : D

Lời giải:

Với $C = 20^{o} C$ ta có: $20 = \frac{5}{9} (F - 32)$

$F - 32 = 36$

$F = 36 + 32 = 68$

Vậy $C = 20^{o} C$ thì ứng với 68 oF

Câu 2 : Biết rằng $4 x - 8 = 0$ . Giá trị của biểu thức $5 x^{2} - 4$ là:

A
$- 24$
B
$24$
C
$- 16$
D
16

Đáp án : D

Lời giải :

$4 x - 8 = 0$

$4 x = 8$

$x = \frac{8}{4} = 2$

Với $x = 2$ thay vào biểu thức $5 x^{2} - 4$ ta có: ${5.2}^{2} - 4 = 16$

Câu 3 : Phương trình $x^{2} + 4 = 0$ có bao nhiêu nghiệm?

A
Vô nghiệm
B
Vô số nghiệm
C
1 nghiệm
D
2 nghiệm

Đáp án : A

Lời giải :

Vì $x^{2} \geq 0$ với mọi x nên $x^{2} + 4 > 0$ với mọi x.

Do đó, phương trình $x^{2} + 4 = 0$ vô nghiệm.

Câu 4 : Nghiệm của phương trình $3 x - 6 = 0$ là:

A
$x = \frac{1}{2}$
B
$x = \frac{- 1}{2}$
C
$x = 2$
D
$x = - 2$

Đáp án : C

Lời giải:

$3 x - 6 = 0$

$3 x = 6$

$x = \frac{6}{3} = 2$

Vậy phương trình có nghiệm $x = 2$

Câu 5 : Nghiệm của phương trình $\frac{3}{4} + \frac{2}{5} x = 0$ có dạng $x = - \frac{a}{b},$ trong đó $b > 0$ và $\frac{a}{b}$ là phân số tối giản. Khẳng định nào sau đây đúng?

A
$a + b = 21$
B
$a + b = 23$
C
$a + b = 20$
D
$a + b = 24$

Đáp án : B

Lời giải:

$\frac{3}{4} + \frac{2}{5} x = 0$

$\frac{2}{5} x = \frac{- 3}{4}$

$x = \frac{- 3}{4} : \frac{2}{5} = \frac{- 15}{8}$

Do đó, $a = 15, b = 8$

Vậy $a + b = 15 + 8 = 23$

Câu 6: Phương trình với ẩn x có dạng:

A
$A (x) = B (x)$ , trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
B
$A (x) > B (x)$ , trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
C
$A (x) < B (x)$ , trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
D
$A (x) \geq B (x)$ , trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x

Đáp án : A

Lời giải :

Phương trình với ẩn x có dạng

$A (x) = B (x)$ , trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x.

Câu 7 : Phương trình nào dưới đây là phương trình một ẩn?

A
$2 x - 2 y + 1 = 0$
B
$x z y = 6$
C
$2 x^{2} + 1 = x - 2$
D
$3 x^{2} + 4 y^{2} = 2 y$

Đáp án : C

Lời giải :

$2 x^{2} + 1 = x - 2$ là phương trình một ẩn (ẩn x)

Câu 8 : $x_{0}$ được gọi là nghiệm của phương trình $A (x) = B (x)$ nếu:

A
$A (x_{0}) < B (x_{0})$
B
$A (x_{0}) > B (x_{0})$
C
$A (x_{0}) \neq B (x_{0})$
D
$A (x_{0}) = B (x_{0})$

Đáp án : D

Lời giải :

Số

$x_{0}$ được gọi là nghiệm của phương trình

$A (x) = B (x)$ nếu giá trị của A(x) và B(x) tại

$x_{0}$ bằng nhau. Tức là

$A (x_{0}) = B (x_{0})$

Câu 9 : Phương trình dạng $a x + b = 0$ , với a, b là hai số đã cho được gọi là phương trình bậc nhất một ẩn x khi:

A
Với mọi giá trị của a, b
B
$a \neq 0; b \neq 0$
C
$a \neq 0$
D
$b \neq 0$

Đáp án : C

Lời giải:

Theo khái niệm về phương trình bậc nhất một ẩn: Phương trình dạng

$a x + b = 0$ , với a, b là hai số đã cho và

$a \neq 0$ được gọi là phương trình bậc nhất một ẩn x.

Câu 10 : Cho phương trình $2 x + 1 = 0$ , chọn khẳng định đúng

A
Hệ số của x là 2, hạng tử tự do là 1
B
Hệ số của x là 1, hạng tử tự do là 2
C
Hệ số của x là $- 1,$ hạng tử tự do là 2
D
Hệ số của x là 2, hạng tử tự do là $- 1$

Đáp án : A

Lời giải:

Phương trình

$2 x + 1 = 0$ có hệ số của x là 2, hạng tử tự do là 1

Câu 11 : Tìm x, biết rằng nếu lấy x trừ đi $\frac{1}{4},$ rồi nhân kết quả với $\frac{1}{2}$ thì được $\frac{1}{8}$

A
$x = \frac{1}{2}$
B
$x = - \frac{1}{2}$
C
$x = \frac{1}{4}$
D
$x = \frac{- 1}{4}$

Đáp án : A

Lời giải :

Theo đề bài ta có: $(x - \frac{1}{4}) . \frac{1}{2} = \frac{1}{8}$

$x - \frac{1}{4} = \frac{1}{8} : \frac{1}{2} = \frac{1}{4}$

$x = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}$

Vậy $x = \frac{1}{2}$

Câu 12 : Gọi $x_{0}$ là nghiệm của phương trình $3 (x - 5) + 9 x (x - 3) = 9 x^{2} .$

Hãy chọn đáp án đúng.

A
$x_{0} < 0$
B
$x_{0} < - 1$
C
$x_{0} > 0$
D
$x_{0} > 1$

Đáp án : A

Lời giải:

$3 (x - 5) + 9 x (x - 3) = 9 x^{2}$

$3 x - 15 + 9 x^{2} - 27 x = 9 x^{2}$

$- 24 x = 15$

$x = \frac{- 5}{8}$

Khi đó, nghiệm của phương là $x_{0} = \frac{- 5}{8}$

Do đó, $x_{0} < 0$

Câu 13 : Cho $A = \frac{2 (x + 1)}{3} - \frac{1}{2}, B = \frac{1 + 3 x}{4}$ . Tìm x để $A = B$

A
$x = 1$
B
$x = - 1$
C
$x = - 2$
D
$x = 2$

Đáp án : B

Lời giải:

Vì $A = B$ nên $\frac{2 (x + 1)}{3} - \frac{1}{2} = \frac{1 + 3 x}{4}$

$\frac{8 (x + 1)}{12} - \frac{6}{12} = \frac{3 (1 + 3 x)}{12}$

$8 x + 8 - 6 = 3 + 9 x$

$9 x - 8 x = 2 - 3$

$x = - 1$

Câu 14 : Cho hai phương trình $8 (x - 2) = 14 + 6 (x - 1) + 2 (x + 5) (1)$ và ${(x - 2)}^{2} = x^{2} - 2 x - 2 (x - 2) (2)$

Hãy chọn đáp án đúng.

A
Phương trình (1) vô nghiệm, phương trình (2) có nghiệm duy nhất
B
Phương trình (1) có vô số nghiệm, phương trình (2) vô nghiệm
C
Phương trình (1) vô nghiệm, phương trình (2) có vô số nghiệm
D
Cả phương trình (1) và phương trình (2) đều có một nghiệm

Đáp án : C

Lời giải :

$8 (x - 2) = 14 + 6 (x - 1) + 2 (x + 5)$

$8 x - 16 = 14 + 6 x - 6 + 2 x + 10$

$8 x - 6 x - 2 x = 18 + 16$

$0 = 34$ (vô lí)

Vậy phương trình (1) vô nghiệm.

${(x - 2)}^{2} = x^{2} - 2 x - 2 (x - 2)$

$x^{2} - 4 x + 4 = x^{2} - 2 x - 2 x + 4$

$x^{2} - 4 x + 4 - x^{2} + 4 x - 4 = 0$

$0 = 0$ (luôn đúng)

Vậy phương trình (2) có vô số nghiệm.

Câu 15 : Cho phương trình: $\frac{x - 11}{2011} + \frac{x - 10}{2012} = \frac{x - 74}{1948} + \frac{x - 72}{1950}$ .

Khẳng định nào sau đây đúng?

A
Nghiệm của phương trình là một chia hết cho 5
B
Nghiệm của phương trình là một số chia hết cho 2
C
Nghiệm của phương trình là một chia hết cho 4
D
Nghiệm của phương trình là một số nguyên tố

Đáp án : B

Lời giải :

$\frac{x - 11}{2011} + \frac{x - 10}{2012} = \frac{x - 74}{1948} + \frac{x - 72}{1950}$

$(\frac{x - 11}{2011} - 1) + (\frac{x - 10}{2012} - 1) = (\frac{x - 74}{1948} - 1) + (\frac{x - 72}{1950} - 1)$

$\frac{x - 2022}{2011} + \frac{x - 2022}{2012} - \frac{x - 2022}{1948} - \frac{x - 2022}{1950} = 0$

$(x - 2022) (\frac{1}{2011} + \frac{1}{2012} - \frac{1}{1948} - \frac{1}{1950}) = 0$

$x - 2022 = 0$ (vì $\frac{1}{2011} + \frac{1}{2012} - \frac{1}{1948} - \frac{1}{1950} < 0$ )

$x = 2022$

Vì 2022 chia hết cho 2, không chia hết cho 4, không chia hết cho 5 nên nghiệm của phương trình là một số chia hết cho 2

Câu 16 : Tìm điều kiện của m để phương trình $3 m x + m - 4 x = 3 m^{2} + 1$ có nghiệm duy nhất

A
$m \neq \frac{4}{3}$
B
$m = \frac{4}{3}$
C
$m = \frac{3}{4}$
D
$m \neq \frac{3}{4}$

Đáp án : A

Lời giải :

$3 m x + m - 4 x = 3 m^{2} + 1$

$(3 m - 4) x + m - 3 m^{2} - 1 = 0$

Để phương trình $(3 m - 4) x + m - 3 m^{2} - 1 = 0$ có nghiệm duy nhất thì $3 m - 4 \neq 0$

$3 m \neq 4$

$m \neq \frac{4}{3}$

Vậy $m \neq \frac{4}{3}$

Câu 17 : Hình tam giác và hình chữ nhật ở hình dưới có cùng chu vi. Khi đó, giá trị của x là:

A
$x = - 2$
B
$x = 2$
C
$x = 1$
D
$x = - 1$

Đáp án : C

Lời giải :

Chu vi hình tam giác là: $x + 2 + x + 4 + x + 5 = 3 x + 11$

Chu vi hình chữ nhật là: $2 (x + 1 + x + 4) = 2 (2 x + 5) = 4 x + 10$

Vì hai hình có chu vi bằng nhau nên: $3 x + 11 = 4 x + 10$

$4 x - 3 x = 11 - 10$

$x = 1$

Câu 18 : Cho hai phương trình $\frac{7 x}{8} - 5 (x - 9) = \frac{1}{6} (20 x + 1, 5) (1)$ và $2 (a - 1) x - a (x - 1) = 2 a + 3 (2)$

Để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) thì giá trị của a là:

A
$a = 7$
B
$a = - 7$
C
$a = \frac{1}{7}$
D
$a = \frac{- 1}{7}$

Đáp án : A

Lời giải:

$\frac{7 x}{8} - 5 (x - 9) = \frac{1}{6} (20 x + 1, 5)$

$\frac{21 x}{24} - \frac{120 (x - 9)}{24} = \frac{4 (20 x + 1, 5)}{24}$

$21 x - 120 x + 1080 = 80 x + 6$

$- 179 x = - 1074$

$x = 6$

Vì phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) nên phương trình (2) có nghiệm là $x = 2$

$2 (a - 1) x - a (x - 1) = 2 a + 3 (2)$

Với $x = 2$ thay vào phương trình (2) ta có:

$2 (a - 1) 2 - a (2 - 1) = 2 a + 3$

$4 a - 4 - a = 2 a + 3$

$a = 7$

Câu 19 : Phương trình $\frac{x + 1}{3} + \frac{3 (2 x + 1)}{4} = \frac{2 x + 3 (x + 1)}{6} + \frac{7 + 12 x}{12}$ có bao nhiêu nghiệm?

A
1 nghiệm
B
2 nghiệm
C
Không có nghiệm nào
D
Có vô số nghiệm

Đáp án : D

Lời giải:

$\frac{x + 1}{3} + \frac{3 (2 x + 1)}{4} = \frac{2 x + 3 (x + 1)}{6} + \frac{7 + 12 x}{12}$

$\frac{4 (x + 1)}{12} + \frac{9 (2 x + 1)}{12} = \frac{2 (5 x + 3)}{12} + \frac{7 + 12 x}{12}$

$4 x + 4 + 18 x + 9 = 10 x + 6 + 7 + 12 x$

$22 x + 13 = 22 x + 13$

$0 = 0$ (luôn đúng)

Vậy phương trình đã cho có vô số nghiệm

Câu 20 : Cho phương trình: $\frac{2 - x}{2001} - 1 = \frac{1 - x}{2002} - \frac{x}{2003} (1)$

Gọi $x_{0}$ là nghiệm của phương trình (1). Chọn đáp án đúng

A
$x_{0} - 3 = 200$
B
$x_{0} - 3 = - 2000$
C
$x_{0} - 3 = 2000$
D
$x_{0} - 3 = - 200$

Đáp án : C

Lời giải:

$\frac{2 - x}{2001} - 1 = \frac{1 - x}{2002} - \frac{x}{2003}$

$\frac{2 - x}{2001} + 1 = (\frac{1 - x}{2002} + 1) + (\frac{- x}{2003} + 1)$

$\frac{2003 - x}{2001} = \frac{2003 - x}{2002} + \frac{2003 - x}{2003}$

$(2003 - x) (\frac{1}{2001} - \frac{1}{2002} - \frac{1}{2003}) = 0$

$2003 - x = 0$ (do $\frac{1}{2001} - \frac{1}{2002} - \frac{1}{2003} \neq 0$ )

$x = 2003$

Do đó phương trình có nghiệm $x_{0} = 2003$ . Vậy $x_{0} - 3 = 2000$

Câu 21 : Cho hình vẽ dưới đây. Biết rằng diện tích của cả hình đó bằng $168 m^{2} .$ Khi đó, giá trị của x (mét) là:

A
11m
B
12m
C
13m
D
14m

Đáp án : B

Lời giải :

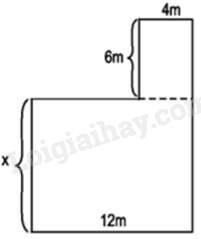
Hình bên có gồm hai hình chữ nhật:

+ Hình chữ nhật độ dài 2 kích thước là 12m và x (mét) nên diện tích hình là: $12 x (m^{2})$

+ Hình chữ nhật có độ dài 2 kích thước là 6m và 4m nên diện tích hình là: $4.6 = 24 (m^{2})$

Mà diện tích của cả hình đó bằng $168 m^{2}$ nên ta có:

$12 x + 24 = 168$

$12 x = 144$

$x = 12$

Vậy $x = 12 m$

Câu 22 : Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là:

A
$48 = 32 (x - 1)$
B
$48 x = 32 (1 - x)$
C
$48 x = 32 (x - 1)$
D
$48 x = 32 (x + 1)$

Đáp án : D

Lời giải chi tiết :

Giả sử ô tô gặp xe máy tại C như trên hình.

Gọi x (giờ) (x > 0) là khoảng thời gian chuyển động của ôtô đi từ A đến C.

Ô tô đi với vận tốc 48km/h nên quãng đường AC bằng: 48.x (km) (1)

Vì xe máy đi trước ôtô 1 giờ nên thời gian xe máy đi từ A đến C bằng: x + 1 (h)

Xe máy đi với vận tốc 32km/h nên quãng đường AC bằng: 32(x + 1) (km) (2)

Từ (1) và (2) ta có phương trình: 48x = 32(x + 1).

Vậy phương trình là: 48x = 32(x + 1).

Câu 23 : Cho phương trình $(m^{2} - 3 m + 2) x = m - 2,$ với m là tham số. Giá trị của m để phương trình có vô số nghiệm là:

A
$m = 1$
B
$m = 2$
C
$m \in {1; 2}$
D
$m = 0$

Đáp án : B

Lời giải:

$(m^{2} - 3 m + 2) x = m - 2 (*)$

Xét $m^{2} - 3 m + 2 = 0$

$m^{2} - m - 2 m + 2 = 0$

$(m - 1) (m - 2) = 0$

Từ đó tính được $m = 1; m = 2$

Với $m = 1$ thay vào (*) ta có: $0. x = - 1$ (vô lí) nên phương trình (*) vô nghiệm.

Với $m = 2$ thay vào (*) ta có: $0 x = 0$ (luôn đúng) nên phương trình (*) có vô số nghiệm với mọi số thực x.

Câu 24 : Số nghiệm của phương trình $\sqrt{x} + 1 = 2 \sqrt{- x}$ là:

A
1 nghiệm
B
2 nghiệm
C
0 nghiệm
D
Vô số nghiệm

Đáp án : C

Lời giải :

Khi $x = 0$ ta có: $1 = 0$ (vô lí) nên $x = 0$ không là nghiệm của phương trình đã cho

Khi $x < 0$ thì $\sqrt{x}$ không xác định

Khi $x > 0$ thì $\sqrt{- x}$ không xác định

Vậy trong mọi trường hợp, không có giá trị nào thỏa mãn phương trình.

Vậy phương trình đã cho vô nghiệm

Câu 25 : Hình dưới dây mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1ft=0,3048m). Tốc độ v(ft/s) của nước tại thời điểm t(s) được cho bởi công thức $v = 48 - 30 t .$ Thời gian để một giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là:

A
1,8s
B
1,7s
C
1,6s
D
1,5s

Đáp án : C

Lời giải :

Khi xuất phát từ mặt đài phun nước, giọt nước có $t = 0.$

Khi giọt nước đạt độ cao tối đa thì $v = 0.$ Thay vào công thức ta có:

$0 = 48 - 30 t$

$30 t = 48$

$t = 1, 6$

Vậy thời gian để giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là: $1, 6 - 0 = 1, 6$ (s)

Câu 26 : Nghiệm của phương trình $\frac{x + a}{b + c} + \frac{x + b}{a + c} + \frac{x + c}{a + b} = - 3$ (các mẫu đều khác 0) là:

A
$x = a + b + c$
B
$x = a - b - c$
C
$x = a + b - c$
D
$x = - (a + b + c)$

Đáp án : D

Lời giải:

$\frac{x + a}{b + c} + \frac{x + b}{a + c} + \frac{x + c}{a + b} = - 3$

$(\frac{x + a}{b + c} + 1) + (\frac{x + b}{a + c} + 1) + (\frac{x + c}{a + b} + 1) = 0$

$\frac{x + a + b + c}{b + c} + \frac{x + a + b + c}{a + c} + \frac{x + a + b + c}{a + b} = 0$

$(x + a + b + c) (\frac{1}{b + c} + \frac{1}{c + a} + \frac{1}{a + b}) = 0$

$x + a + b + c = 0$

$x = - (a + b + c)$

Vậy nghiệm của phương trình đã cho là $x = - (a + b + c)$

Câu 27 : Cho a và ba số b, c, d khác a thỏa mãn điều kiện $b + d = 2 c .$ Số nghiệm của phương trình $\frac{x}{(a - b) (a - c)} - \frac{2 x}{(a - b) (a - d)} + \frac{3 x}{(a - c) (a - d)} = \frac{4 a}{(a - c) (a - d)}$ là:

A
0 nghiệm
B
1 nghiệm
C
2 nghiệm
D
Vô số nghiệm

Đáp án : B

Lời giải :

$\frac{x}{(a - b) (a - c)} - \frac{2 x}{(a - b) (a - d)} + \frac{3 x}{(a - c) (a - d)} = \frac{4 a}{(a - c) (a - d)}$

$\frac{x (a - d) - 2 x (a - c) + 3 x (a - b)}{(a - b) (a - c) (a - d)} = \frac{4 a (a - b)}{(a - b) (a - c) (a - d)}$

$x (a - d - 2 a + 2 c + 3 a - 3 b) = 4 a (a - b)$

$x (2 a - 3 b + 2 c - d) = 4 a (a - b) (1)$

Từ giả thiết, $b + d = 2 c$ nên $2 a - 3 b + 2 c - d = 2 a - 2 b = 2 (a - b)$ thay vào (1) ta có:

$2 (a - b) x = 4 a (a - b) (2)$

Vì $a - b \neq 0$ nên phương trình (2) có nghiệm duy nhất là $x = 2 a .$

Vậy phương trình đã cho có một nghiệm.

Câu 28 : Cho phương trình $0, 05 (\frac{2 x - 2}{2009} + \frac{2 x}{2010} + \frac{2 x + 2}{2011}) = 3, 3 - (\frac{x - 1}{2009} + \frac{x}{2010} + \frac{x + 1}{2011})$

Hãy chọn đáp án đúng.

A
Nghiệm của phương trình đã cho là số chẵn
B
Nghiệm của phương trình đã cho là số lẻ
C
Nghiệm của phương trình đã cho là chính phương
D
Nghiệm của phương trình đã cho là số nguyên tố

Đáp án : A

Lời giải :

$0, 05 (\frac{2 x - 2}{2009} + \frac{2 x}{2010} + \frac{2 x + 2}{2011}) = 3, 3 - (\frac{x - 1}{2009} + \frac{x}{2010} + \frac{x + 1}{2011})$

$\frac{x - 1}{2009} + \frac{x}{2010} + \frac{x + 1}{2011} = 3$

$(\frac{x - 1}{2009} - 1) + (\frac{x}{2010} - 1) + (\frac{x + 1}{2011} - 1) = 0$

$\frac{x - 2010}{2009} + \frac{x - 2010}{2010} + \frac{x - 2010}{2011} = 0$

$(x - 2010) (\frac{1}{2009} + \frac{1}{2010} + \frac{1}{2011}) = 0$

$x - 2010 = 0$

$x = 2010$

Do đó, nghiệm của phương trình là một số chẵn.

1 174 lượt xem

Bài trước

Bài sau

30 câu Trắc nghiệm Phương trình bậc nhất một ẩn (có đáp án 2024) – Toán 8 Kết nối tri thức

Giới thiệu

Liên kết

Chính sách

Kết nối

30 câu Trắc nghiệm Phương trình bậc nhất một ẩn (có đáp án 2024) – Toán 8 Kết nối tri thức

CHỌN BỘ SÁCH BẠN MUỐN XEM