Lý thuyết Ba trường hợp đồng dạng của hai tam giác (Kết nối tri thức 2024) Toán 8

Lý thuyết Toán lớp 8 Bài 34: Ba trường hợp đồng dạng của hai tam giác

A. Lý thuyết Ba trường hợp đồng dạng của hai tam giác

1. Trường hợp đồng dạng thứ nhất của tam giác

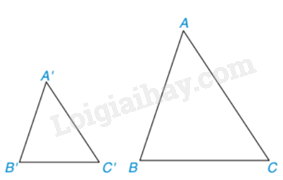
Trường hợp đồng dạng cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.

$\{\begin{array}{l}\mathrm{\Delta }ABC,\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime };\\ \frac{A^{\prime }{B}^{\prime }}{AB}=\frac{B^{\prime }{C}^{\prime }}{BC}=\frac{A^{\prime }{C}^{\prime }}{AC}\end{array}\Rightarrow \mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }\backsim \mathrm{\Delta }ABC$

2. Trường hợp đồng dạng thứ hai của tam giác

Trường hợp đồng dạng cạnh – góc – cạnh:

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.

$\{\begin{array}{l}\mathrm{\Delta }ABC,\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime };\\ \frac{A^{\prime }{B}^{\prime }}{AB}=\frac{A^{\prime }{C}^{\prime }}{AC},\widehat{A^{\prime }}=\hat{A}\end{array}\Rightarrow \mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }\backsim \mathrm{\Delta }ABC$

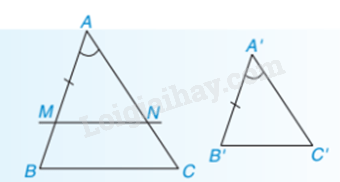
Nhận xét: Nếu $\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }\backsim \mathrm{\Delta }ABC$ theo tỉ số k và AM, A’M’ lần lượt là các đường trung tuyến của $\mathrm{\Delta }ABC$ và $\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }$ thì $\frac{A^{\prime }{M}^{\prime }}{AM}=k$

3. Trường hợp đồng dạng thứ ba của tam giác

Trường hợp đồng dạng góc – góc:

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

$\{\begin{array}{l}\mathrm{\Delta }ABC,\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime };\\ \widehat{A^{\prime }}=\hat{A},\widehat{B^{\prime }}=\hat{B}\end{array}\Rightarrow \mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }\backsim \mathrm{\Delta }ABC$

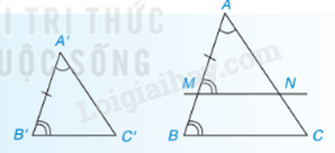
Nhận xét: $\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }\backsim \mathrm{\Delta }ABC$ theo tỉ số k và AM, A’M’ lần lượt là các đường phân giác của $\mathrm{\Delta }ABC$ và $\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }$ thì $\frac{A^{\prime }{M}^{\prime }}{AM}=k$

Sơ đồ tư duy Ba trường hợp đồng dạng của hai tam giác

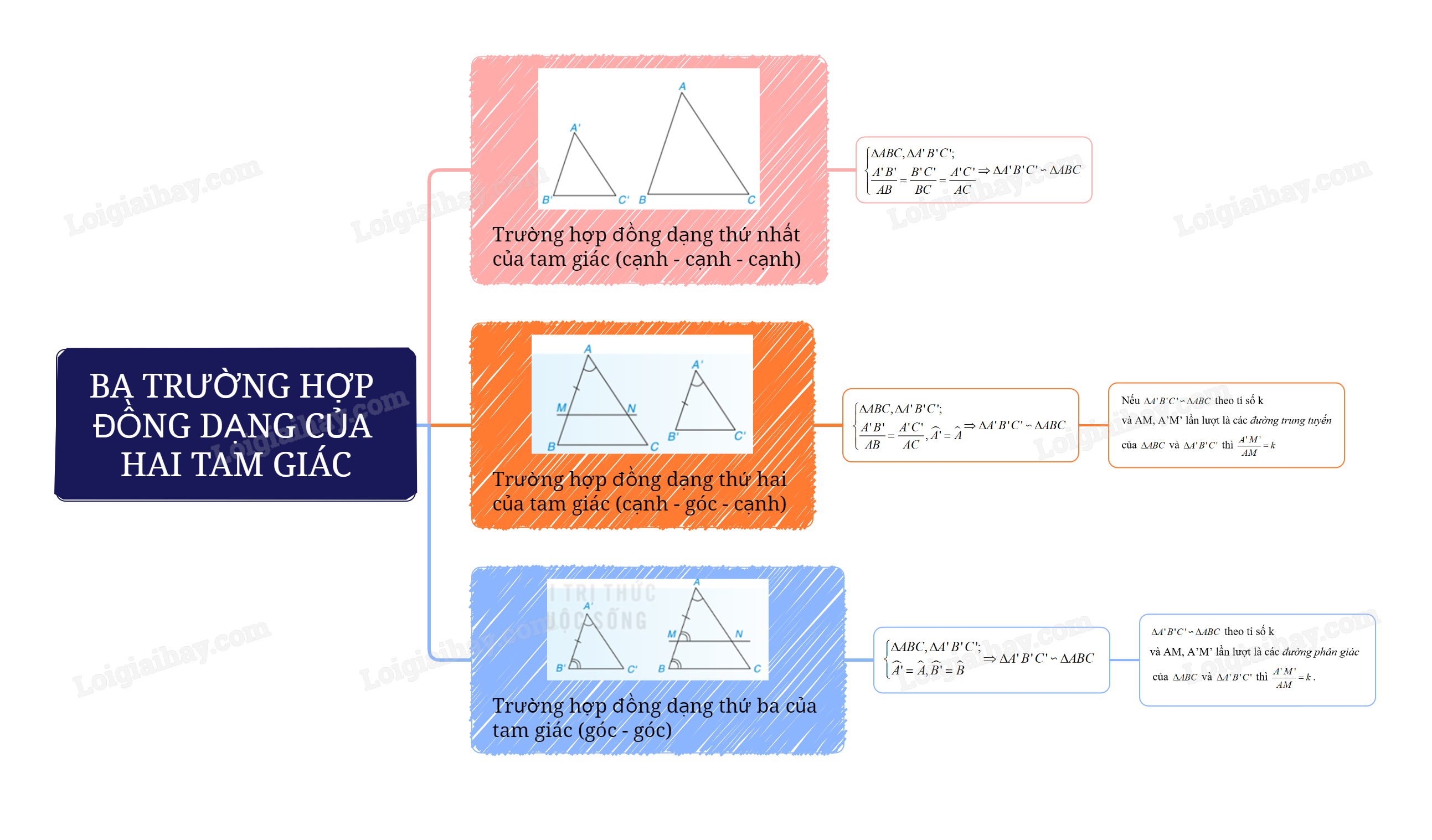
B. Bài tập Ba trường hợp đồng dạng của hai tam giác

Đang cập nhật...