Lý thuyết Tứ giác (Kết nối tri thức 2024) Toán 8

Lý thuyết Toán lớp 8 Bài 10: Tứ giác

A. Lý thuyết Tứ giác

1. Khái niệm 

Tứ giác ABCD là một hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

Ví dụ:

Đặc điểm

+ Có 4 đỉnh

+ Có 4 cạnh

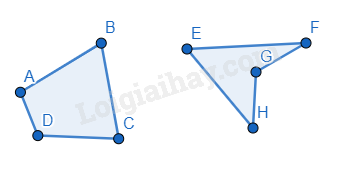
Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa bất kỳ cạnh nào của tứ giác đó.

Ví dụ: ABCD là tứ giác lồi, EFGH không phải là tứ giác lồi.

2. Tính chất

+ Hai cạnh kề nhau là hai cạnh chung đỉnh.

+ Hai cạnh kề nhau tạo thành góc của tứ giác.

+ Hai cạnh đối nhau không chung đỉnh.

+ Hai đỉnh đối nhau là hai đỉnh không cùng nằm trên một cạnh.

+ Đường chéo là đoạn thẳng nối hai đỉnh đối nhau.

3. Định lí tổng các góc của một tứ giác

Tổng số đo các góc của một tứ giác bằng ${360}^0$.

Tứ giác ABCD, $\hat{A}+\hat{B}+\hat{C}+\hat{D}={360}^0$

Ví dụ:

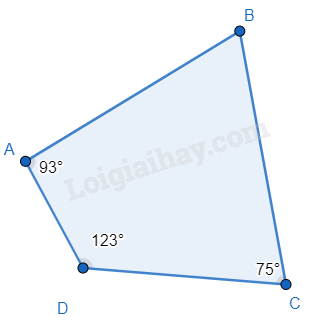
$\hat{B}={360}^0-{93}^0-{123}^0-{75}^0={69}^0$

B. Bài tập Tứ giác

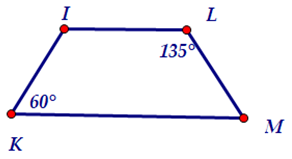
Bài 1. Tính góc chưa biết của tứ giác trong hình dưới đây, biết $\hat{I}+\hat{K}=180°$ .

Hướng dẫn giải

Vì $\hat{I}+\hat{K}=180°$mà $\hat{K}=60°\Rightarrow \hat{I}=120°$

Theo định lí về tổng các góc trong một tứ giác ta có:

$\hat{I}+\hat{K}+\hat{M}+\hat{L}=360°\Rightarrow \hat{M}=360°-(\hat{I}+\hat{K}+\hat{L})=360°-(120°+60°+135°)=45°$.

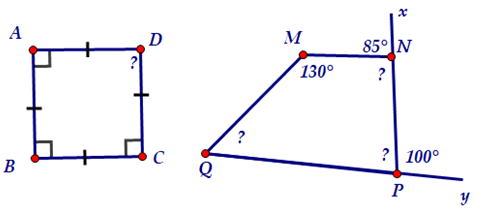
Bài 2. Tính góc chưa biết của các tứ giác trong hình sau:

Hướng dẫn giải

+ Tứ giác ABCD có 3 góc vuông nên $\hat{A}=\hat{B}=\hat{C}=90°$. Theo định lí về tổng các góc trong một tứ giác ta có: $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$

Suy ra $\hat{D}=360°-(\hat{A}+\hat{B}+\hat{C})=360°-(90°+90°+90°)=90°.$

+ Vì $\widehat{MNx}+\widehat{MNP}=180°$(hai góc kề bù)$\Rightarrow \widehat{MNP}=180°-85°=95°.$

$\widehat{NPy}+\widehat{NPQ}=180°$(hai góc kề bù) $\Rightarrow \widehat{NPQ}=180°-100°=80°.$

Theo định lí về tổng các góc trong một tứ giác ta có:$\hat{M}+\widehat{MNP}+\widehat{NPQ}+\hat{Q}=360°$

Suy ra $\hat{Q}=360°-(\hat{M}+\widehat{MNP}+\widehat{NPQ})=360°-130°-95°-80°=55°$.

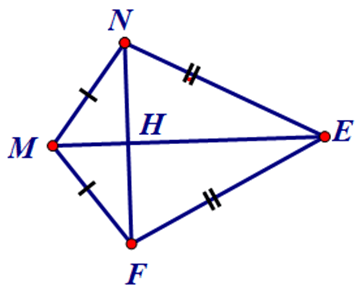
Bài 3. Tứ giác MNEF có MN = MF, NE = FE, được gọi là hình cái diều.

a) Chứng minh ME là đường trung trực của đoạn thẳng NF.

b) Tính các góc E, F biết $\hat{M}=100°,\hat{N}=105°.$

Hướng dẫn giải

a) Xét $\Delta MNE$ và $\Delta MFE$  có:

MN = MF$\Rightarrow NH=FH$ (giả thiết)

NE = FE (giả thiết)

ME chung

Do đó $\Delta MNE$  = $\Delta MFE$  (cạnh - cạnh - cạnh) $\Rightarrow \widehat{FME}=\widehat{NME}$

Gọi H là giao điểm của ME và NF

Xét $\Delta MNH$và $\Delta MFH$  có:

MN = MF ( giả thiết)

$\widehat{FME}=\widehat{NME}$ (chứng minh trên)

MH chung

Do đó $\Delta MNH$ = $\Delta MFH$  (cạnh - góc - cạnh)

$\Rightarrow NH=FH$(1)

Và $\widehat{MHN}=\widehat{MHF}$  mà $\widehat{MHN}+\widehat{MHF}=180°\Rightarrow \widehat{MHN}=\widehat{MHF}=90°$

$\Rightarrow ME\perp NF$(2)

Từ (1) và (2) suy ra ME là đường trung trực của đoạn thẳng NF.

b) Vì $\Delta MNE=\Delta MFE\Rightarrow \widehat{MNE}=\widehat{MFE}=105°$

Theo định lí về tổng các góc trong một tứ giác suy ra $\widehat{NEF}=50°$.