Lý thuyết Phân tích đa thức thành nhân tử (Kết nối tri thức 2024) Toán 8

Lý thuyết Toán lớp 8 Bài 9: Phân tích đa thức thành nhân tử

A. Lý thuyết Phân tích đa thức thành nhân tử

Phân tích đa thức thành nhân tử:

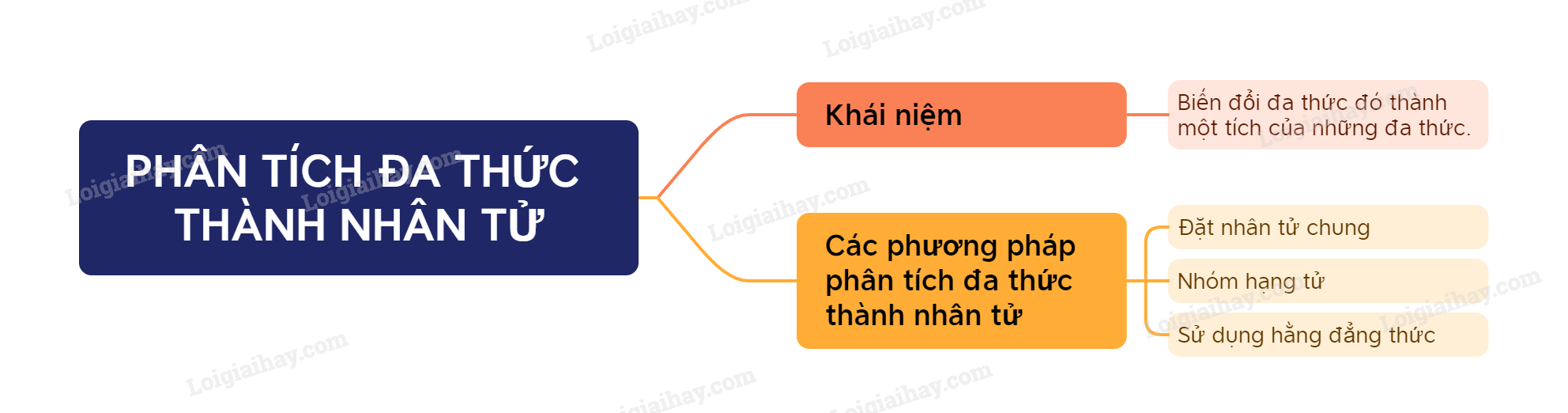
Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

Phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung:

Ví dụ: Phân tích đa thức $x^3+x$ thành nhân tử: $x^3+x=x.x^2+x=x(x^2+1)$

Phân tích đa thức thành nhân tử bằng cách nhóm nhân tử:

Ví dụ: Phân tích đa thức $xy+3z+xz+3y$ thành nhân tử:

 $xy+3z+xz+3y=(xy+xz)+(3z+3y)=x(y+z)+3(z+y)=(x+3)(y+z)$

Phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức như thế nào?

Ví dụ: Phân tích đa thức $x^2-8x+16$ thành nhân tử: $x^2-8x+16=x^2-2.x.4+4^2=(x-4{)}^2$

B. Bài tập Phân tích đa thức thành nhân tử

Bài 1. Tìm x, biết:

a) 2x2 + 2x = 0;                                          

b) 3x3 – 3x = 0.

Hướng dẫn giải

a) Ta có: 2x2 + 2x = 2x(x + 1)

Khi đó, 2x2 + 2x = 0 thì 2x(x + 1) = 0.

TH1: 2x = 0, suy ra x = 0.

TH2: x + 1 = 0, suy ra x = – 1.

Vậy x = 0 hoặc x = – 1.

b) Ta có: 3x3 – 3x = 3x(x2 – 1) = 3x(x – 1)(x + 1).

Khi đó 3x3 – 3x = 0 thì 3x(x + 1)(x – 1) = 0.

TH1: 3x = 0, suy ra x = 0.

TH2: x + 1 = 0, suy ra x = – 1.

TH3: x – 1 = 0, suy ra x = 1.

Vậy x = 0 hoặc x = – 1 hoặc x = 1.

Bài 2. Phân tích các đa thức sau thành nhân tử:

a) 3x2 + xy;                                                

b) 4x3 – x;

c) x2 – 16 + xy – 4y;                                  

d) 8x4 – x.

Hướng dẫn giải

a) 3x2 + xy = x(3x + y); 

b) 4x3 – x = x(4x2 – 1) = x[(2x)2 – 12] = x(2x – 1)(2x + 1);

c) x2 – 16 + xy – 4y = (x2 – 16) + (xy – 4y)

                             = (x – 4)(x + 4) + y(x – 4)

                             = (x – 4)(x + 4 + y);

d) 8x4 – x = x(8x3 – 1) = x[(2x)3 – 13]

                = x(2x – 1)(4x2 + 2x + 1).

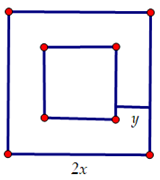
Bài 3. Một khu vườn hình vuông có độ dài cạnh bằng 2x (mét). Người ta làm đường đi xung quanh khu vườn, có độ rộng như nhau và bằng y (mét).

a) Viết biểu thức tính diện tích S của đường đi bao quanh mảnh vườn theo x và y.

b) Phân tích S thành nhân tử rồi tính S khi x = 102 m, y = 4 m.

Hướng dẫn giải

a) Diện tích khu vườn hình vuông là: (2x)2 (m2).

Vì làm đường đi bao quanh khu vườn, mỗi bên có độ rộng y mét nên phần vườn không chứa đường đi là một hình vuông có cạnh là 2x – 2y (m).

Diện tích khu vườn hình vuông sau khi làm đường đi là: (2x – 2y)2 (m2).

Diện tích đường đi bao quanh khu vườn là: S = (2x)2 – (2x – 2y)2 (m2).

b) Ta có:

S = (2x)2 – (2x – 2y)2

= [2x – (2x – 2y)][2x + (2x – 2y)]

= (2x – 2x + 2y)(2x + 2x – 2y)

= 2y(4x – 2y)

= 4y(2x – y).

Thay x = 102 m, y = 4 m vào S ta được:

S = 4.4.(2.102 – 4) = 16.200 = 3 200 m2.