Lý thuyết Khái niệm hàm số và đồ thị của hàm số (Kết nối tri thức 2024) Toán 8

Lý thuyết Toán lớp 8 Bài 27: Khái niệm hàm số và đồ thị của hàm số

A. Lý thuyết Khái niệm hàm số và đồ thị của hàm số

1. Hàm số

Khái niệm:

Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.

Ví dụ: Ta có bảng nhiệt độ dự báo ở Thủ đô Hà Nội ngày 25/5/2023.

Ta có nhiệt độ T là hàm số của thời điểm t vì mỗi giá trị của t chỉ xác định đúng một giá trị của T.

Ngược lại, thời điểm t không phải là hàm số của nhiệt độ T, vì nhiệt độ T = 340C tương ứng với hai thời điểm khác nhau t = 12 và t = 13.

Chú ý: Khi y là hàm số của x, ta viết $y=f(x);y=g(x),...$

Ví dụ: Cho hàm số y = f(x) = x + 3.

f(-2) = -2 + 3 = 1;            f(0) = 0 + 3 = 3

2. Mặt phẳng tọa độ

Khái niệm: Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ.

• Ox nằm ngang gọi là trục hoành;
• Oy thẳng đứng gọi là trục tung;
• O gọi là gốc tọa độ.

Tọa độ của một điểm:

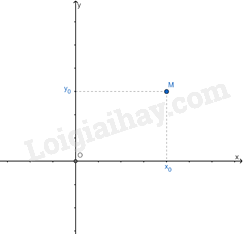
Trong mặt phẳng tọa độ, mỗi điểm M xác định duy nhất một cặp số $(x_0;y_0)$ và mỗi cặp số $(x_0;y_0)$ xác định duy nhất một điểm M.

Cặp số $(x_0;y_0)$ gọi là tọa độ của M, kí hiệu là M(x0,y0), trong đó x0 là hoành độ, y0 là tung độ của điểm M.

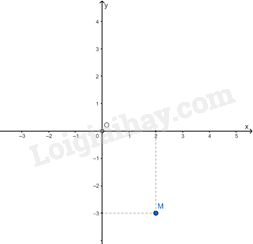
Ví dụ: Điểm M có tọa độ là (2; -3), kí hiệu là M(2; -3). Số 2 gọi là hoành độ, số -3 gọi là tung độ của điểm M.

3. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; y) trên mặt phẳng tọa độ.

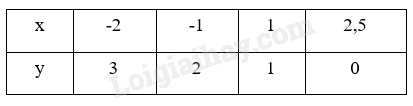
Ví dụ: Đồ thị của hàm số y = f(x) cho bởi bảng:

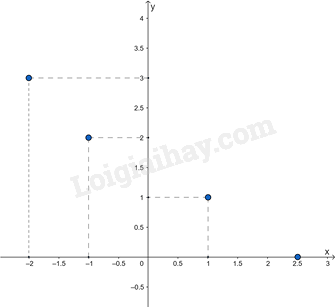
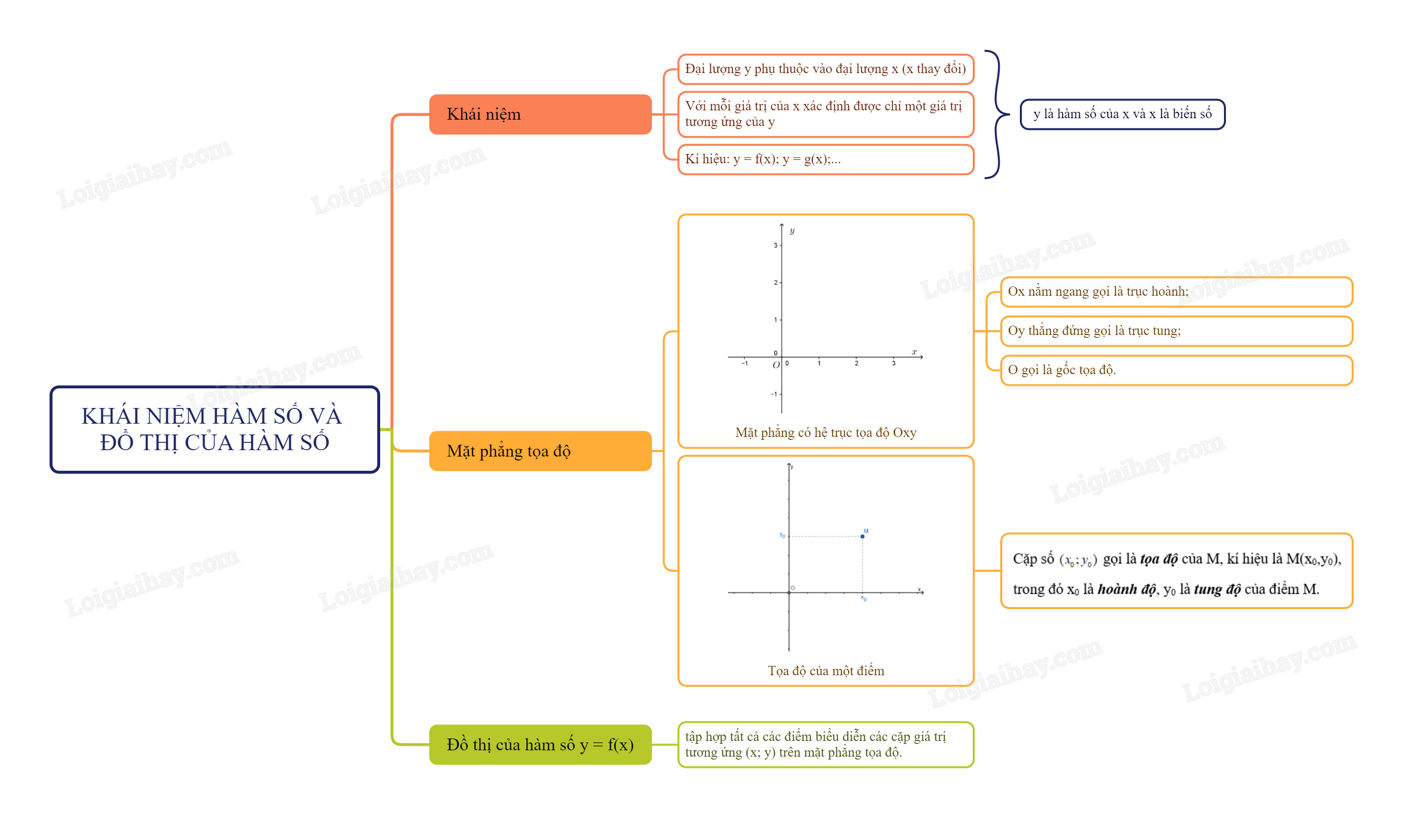
Sơ đồ tư duy Khái niệm hàm số và đồ thị của hàm số

B. Bài tập Khái niệm hàm số và đồ thị của hàm số

Đang cập nhật...