50 câu Trắc nghiệm Dấu của tam thức bậc hai (có đáp án 2024) – Toán 10 Chân trời sáng tạo
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 1: Dấu của tam thức bậc hai đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 1.
Trắc nghiệm Toán 10 Bài 1: Dấu của tam thức bậc hai
I. Nhận biết
Câu 1. Cho f(x) = ax2 + bx + c (a ≠ 0) và ∆ = b2 – 4ac. Khi f(x) luôn cùng dấu với hệ số a, với mọi x ∈ ℝ thì:
A. ∆ < 0;
B. ∆ = 0;
C. ∆ > 0;
D. ∆ ≥ 0.
Hướng dẫn giải
Đáp án: A
Giải thích:
Ta có f(x) cùng dấu với hệ số a với mọi giá trị của x khi ∆ < 0.
Do đó ta chọn phương án A.
Câu 6. Cho f(x) = (3m – 2)x2 – 2(3m – 2)x + 3(2m + 1). Đa thức f(x) là tam thức bậc hai khi và chỉ khi:
A. m<23;
B. m≠23;
C. m>23;
D. m=23.
Hướng dẫn giải
Đáp án: B
Giải thích:
Ta có đa thức f(x) = (3m – 2)x2 – 2(3m – 2)x + 3(2m + 1) là tam thức bậc hai khi và chỉ khi a ≠ 0.
Nghĩa là, 3m – 2 ≠ 0.
Suy ra m≠23.
Vậy ta chọn phương án B.
Câu 3. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0). Khẳng định nào sau đây đúng?
A. Nếu ∆ > 0 thì f(x) luôn cùng dấu với hệ số a, ∀x ∈ ℝ;
B. Nếu ∆ < 0 thì f(x) luôn trái dấu với hệ số a, ∀x ∈ ℝ;
C. Nếu ∆ = 0 thì f(x) luôn cùng dấu với hệ số a, ∀x ∈ ℝ \ {−b2a};
D. Nếu ∆ < 0 thì f(x) luôn cùng dấu với hệ số b, ∀x ∈ ℝ.
Hướng dẫn giải
Đáp án: C
Giải thích:
Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0), ta có:
⦁ Nếu ∆ < 0 thì f(x) cùng dấu với a với mọi giá trị x.
Do đó phương án B, D đều sai.
⦁ Nếu ∆ = 0 và x0=−b2a là nghiệm kép của f(x) thì f(x) cùng dấu với a với mọi x ≠ x0.
Do đó phương án C đúng.
⦁ Nếu ∆ > 0 và x1, x2 là hai nghiệm của f(x) (x1 < x2) thì f(x) trái dấu với a với mọi x trong khoảng (x1; x2); f(x) cùng dấu với a với mọi x thuộc hai khoảng (–∞; x1); (x2; +∞).
Do đó phương án A sai.
Vậy ta chọn phương án C.
Câu 4. Biểu thức nào sau đây là tam thức bậc hai?
A. f(x) = 2x3 + 3x2 + 1;
B. f(x) = –x2 + 2x – 10;
C. f(x) = x – 4;
D. f(x) = –7.
Hướng dẫn giải
Đáp án: B
Giải thích:
Tam thức bậc hai có dạng f(x) = ax2 + bx + c, với a ≠ 0.
Ta thấy chỉ có đa thức ở phương án B có dạng f(x) = ax2 + bx + c với a = –1, b = 2 và c = –10.
Vậy ta chọn phương án B.
Câu 5. Biệt thức và biệt thức thu gọn của tam thức bậc hai f(x) = –x2 – 4x – 6 lần lượt là:
A. ∆ = –2 và ∆’ = –8;
B. ∆’ = –8 và ∆ = –2;
C. ∆ = 8 và ∆’ = 2;
D. ∆ = –8 và ∆’ = –2.
Hướng dẫn giải
Đáp án: D
Giải thích:
Tam thức bậc hai f(x) = –x2 – 4x – 6 có dạng f(x) = ax2 + bx + c, với a = –1, b = –4, c = –6.
Biệt thức của f(x): ∆ = b2 – 4ac = (–4)2 – 4.(–1).(–6) = –8.
Biệt thức thu gọn của f(x): ∆’ = (b2)2−ac=(−42)2−(−1).(−6)=−2.
Vậy ∆ = –8 và ∆’ = –2.
Do đó ta chọn phương án D.
Câu 6. Cho tam thức f(x) = ax2 + bx + c (a ≠ 0), có ∆ = b2 – 4ac. Ta có f(x) ≤ 0, ∀x ∈ ℝ khi và chỉ khi:
A. a < 0 và ∆ ≤ 0;
B. a ≤ 0 và ∆ < 0;
C. a < 0 và ∆ ≥ 0;
D. a > 0 và ∆ ≤ 0.
Hướng dẫn giải
Đáp án: A
Giải thích:
Ta có f(x) ≤ 0, ∀x ∈ ℝ khi và chỉ khi a < 0 và ∆ ≤ 0.
Ta chọn phương án A.
Câu 7. Nghiệm của tam thức bậc hai f(x) = –2x2 + 4x – 2 là:
A. x = 1;
B. x = 1 hoặc x = –1;
C. x = –1;
D. f(x) vô nghiệm.
Hướng dẫn giải
Đáp án: A
Giải thích: Ư
Tam thức bậc hai f(x) = –2x2 + 4x – 2 có ∆ = 42 – 4.(–2).(–2) = 0.
Do đó f(x) có nghiệm kép x=−42.(−2)=1.
Vậy f(x) có nghiệm là x = 1.
Do đó ta chọn phương án A.
II. Thông hiểu
Câu 1. Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình vẽ.
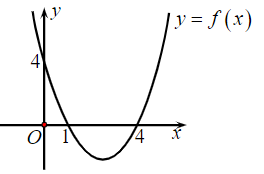
Đặt ∆ = b2 – 4ac. Chọn khẳng định đúng?
A. a > 0, ∆ > 0;
B. a < 0, ∆ > 0;
C. a > 0, ∆ = 0;
D. a < 0, ∆ = 0.
Hướng dẫn giải
Đáp án: A
Giải thích:
Quan sát đồ thị, ta thấy:
⦁ Đồ thị y = f(x) cắt trục Ox tại hai điểm phân biệt có hoành độ lần lượt là x1 = 1; x2 = 4.
Suy ra f(x) có 2 nghiệm phân biệt x1 = 1; x2 = 4.
Do đó ∆ > 0.
⦁ Trên khoảng (–∞; 1) và (4; +∞), ta có f(x) > 0. Suy ra a > 0.
Vậy ta có a > 0, ∆ > 0.
Ta chọn phương án A.
Câu 2. Cho tam thức bậc hai f(x) = x2 – 10x + 2. Kết luận nào sau đây đúng?
A. f(–2) < 0;
B. f(1) > 0;
C. f(–2) > 0;
D. f(1) = 0.
Hướng dẫn giải
Đáp án: C
Giải thích:
Ta có:
⦁ f(1) = 12 – 10.1 + 2 = –7 < 0.
Do đó phương án B, D sai.
⦁ f(–2) = (–2)2 – 10.(–2) + 2 = 26 > 0.
Do đó phương án C đúng, phương án A sai.
Vậy ta chọn phương án C.
Câu 3. Cho tam thức bậc hai f(x) = –2x2 + 8x – 8. Trong các mệnh đề sau, mệnh đề nào đúng?
A. f(x) < 0, ∀x ∈ ℝ;
B. f(x) ≥ 0, ∀x ∈ ℝ;
C. f(x) ≤ 0, ∀x ∈ ℝ;
D. f(x) > 0, ∀x ∈ ℝ.
Hướng dẫn giải
Đáp án: C
Giải thích:
Tam thức bậc hai f(x) = –2x2 + 8x – 8 có ∆ = 82 – 4.(–2).(–8) = 0.
Suy ra f(x) có nghiệm kép x=−82.(−2)=2.
Ta có a = –2 < 0.
Do đó f(x) < 0 với mọi x ≠ 2
Hay f(x) ≤ 0 với mọi x ∈ ℝ.
Do đó ta chọn phương án C.
Câu 4. Cho hàm số y = f(x) có đồ thị như hình bên.
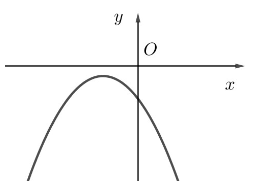
Bảng xét dấu của tam thức bậc hai tương ứng là:
A.
|
x |
–∞ +∞ |
|
f(x) |
+ |
|
x |
–∞ –1 +∞ |
|
f(x) |
+ 0 + |
|
x |
–∞ +∞ |
|
f(x) |
– |
|
x |
–∞ –1 +∞ |
|
f(x) |
– 0 – |
Đáp án: C
Giải thích:
Quan sát đồ thị, ta thấy f(x) < 0, với mọi x ∈ ℝ.
Do đó ta có bảng xét dấu của f(x) như sau:
|
x |
–∞ +∞ |
|
f(x) |
– |
Vậy ta chọn phương án C.
Câu 5. Bảng xét dấu nào sau đây là của f(x) = 6x2 + 37x + 6?
A.
|
x |
–∞ –6 −16 +∞ |
|
f(x) |
– 0 + 0 – |
|
x |
–∞ –6 −16 +∞ |
|
f(x) |
+ 0 – 0 + |
|
x |
–∞ -12 +∞ |
|
f(x) |
+ 0 + |
|
x |
–∞ +∞ |
|
f(x) |
+ |
Đáp án: B
Giải thích:
Tam thức bậc hai f(x) = 6x2 + 37x + 6 có ∆ = 372 – 4.6.6 = 1225 > 0.
Do đó f(x) có hai nghiệm phân biệt là:
x1=−37+√12252.6=−16; x2=−37−√12252.6=−6
Ta có a = 6 > 0.
Ta có bảng xét dấu f(x) như sau:
|
x |
–∞ –6 −16 +∞ |
|
f(x) |
+ 0 – 0 + |
Vậy ta chọn phương án B.
Câu 6. Cho tam thức bậc hai f(x) = x2 – 8x + 16. Khẳng định nào sau đây đúng?
A. Phương trình f(x) = 0 vô nghiệm;
B. f(x) > 0, ∀x ∈ ℝ;
C. f(x) ≥ 0, ∀x ∈ ℝ;
D. f(x) < 0 khi x < 4.
Hướng dẫn giải
Đáp án: C
Giải thích:
Tam thức bậc hai f(x) = x2 – 8x + 16 có ∆ = (–8)2 – 4.1.16 = 0.
Do đó f(x) có nghiệm kép x=−−82.1=4.
Khi đó phương án A sai.
Ta có a = 1 > 0.
Vì vậy f(x) > 0 với mọi x ≠ 4 hay f(x) ≥ 0, với mọi x ∈ ℝ.
Do đó phương án B và D sai; phương án C đúng.
Vậy ta chọn phương án C.
Câu 7. Tam thức nào sau đây luôn dương với mọi giá trị của x?
A. f(x) = x2 – 10x + 2;
B. f(x) = x2 – 2x + 1;
C. f(x) = x2 – 2x + 10;
D. f(x) = –x2 + 2x + 10.
Hướng dẫn giải
Đáp án: C
Giải thích:
Tam thức f(x) luôn dương với mọi giá trị của x khi và chỉ khi a > 0 và ∆ < 0.
⦁ Xét phương án A: f(x) = x2 – 10x + 2.
Ta có a = 1 > 0 và ∆ = (–10)2 – 4.1.2 = 92 > 0.
Do đó ta loại phương án A.
⦁ Xét phương án B: f(x) = x2 – 2x + 1.
Ta có a = 1 > 0 và ∆ = (–2)2 – 4.1.1 = 0.
Do đó ta loại phương án B.
⦁ Xét phương án C: f(x) = x2 – 2x + 10.
Ta có a = 1 > 0 và ∆ = (–2)2 – 4.1.10 = –36 < 0.
Do đó ta nhận phương án C.
⦁ Xét phương án D: f(x) = –x2 + 2x + 10.
Ta có a = –1 < 0.
Do đó ta loại phương án D.
Vậy ta chọn phương án C.
Câu 8. Cho tam thức bậc hai f(x) = x2 + 1. Mệnh đề nào sau đây đúng nhất?
A. f(x) > 0 ⇔ x ∈ (–∞; +∞);
B. f(x) = 0 ⇔ x = –1;
C. f(x) < 0 ⇔ x ∈ (–∞; 1);
D. f(x) > 0 ⇔ x ∈ (0; 1).
Hướng dẫn giải
Đáp án: A
Giải thích:
Tam thức bậc hai f(x) = x2 + 1 có ∆ = 02 – 4.1.1 = –4 < 0.
Suy ra f(x) vô nghiệm.
Ta có a = 1 > 0.
Vậy f(x) > 0, ∀x ∈ ℝ hay f(x) > 0 ⇔ x ∈ (–∞; +∞).
Ta chọn phương án A.
III. Vận dụng
Câu 1. Cho f(x) = (m – 3)x2 + (m + 3)x – (m + 1). Để f(x) là một tam thức bậc hai và có nghiệm kép thì:
A. m = 1;
B. m = –1;
C. m=−35;
D. Cả A và C đều đúng.
Hướng dẫn giải
Đáp án: D
Giải thích:
Xét f(x) = (m – 3)x2 + (m + 3)x – (m + 1).
Ta có:
∆ = (m + 3)2 – 4.(m – 3).[–(m + 1)]
= m2 + 6m + 9 + 4.(m – 3)(m + 1)
= m2 + 6m + 9 + 4(m2 – 2m – 3)
= 5m2 – 2m – 3.
Ta có f(x) là một tam thức bậc hai và có nghiệm kép khi và chỉ khi a ≠ 0 và ∆ = 0.
⇔{m–
Vậy ta chọn phương án D.
Câu 2. Cho f(x) = x2 + 2(m – 1)x + m2 – 3m + 4. Giá trị của m để f(x) không âm với mọi giá trị của x là:
A. m < 3;
B. m ≥ 3;
C. m ≤ –3;
D. m ≤ 3.
Hướng dẫn giải
Đáp án: D
Giải thích:
Xét f(x) = x2 + 2(m – 1)x + m2 – 3m + 4.
Ta có:
∆’ = (m – 1)2 – 1.(m2 – 3m + 4)
= m2 – 2m + 1 – m2 + 3m – 4
= m – 3.
Yêu cầu bài toán ⇔ Tìm m để f(x) ≥ 0 với mọi giá trị của x.
Ta có f(x) ≥ 0, với mọi giá trị của x.
⇔ a > 0 và ∆’ ≤ 0.
⇔ 1 > 0 (luôn đúng) và m – 3 ≤ 0.
⇔ m ≤ 3.
Vậy m ≤ 3 thỏa mãn yêu cầu bài toán.
Ta chọn phương án D.
Câu 3. Cho f(x) = mx2 + 2(m + 1)x + m – 2. Với giá trị nào của tham số m thì f(x) là tam thức bậc hai và f(x) > 0 có nghiệm?
A. m ∈ ℝ;
B. ;
C. m ∈ ;
D. m ∈ ℝ \ {0}.
Hướng dẫn giải
Đáp án: C
Giải thích:
f(x) = mx2 + 2(m + 1)x + m – 2 là tam thức bậc hai ⇔ a ≠ 0 ⇔ m ≠ 0.
Ta có:
∆’ = (m + 1)2 – m(m – 2)
= m2 + 2m + 1 – m2 + 2m
= 4m + 1.
Trường hợp 1: a > 0 ⇔ m > 0.
Khi đó f(x) > 0 có nghiệm với mọi x.
Do đó m > 0 thỏa mãn yêu cầu đề bài.
Trường hợp 2: a < 0 ⇔ m < 0.
Khi đó để f(x) > 0 có nghiệm thì ∆ > 0.
⇔ 4m + 1 > 0.
⇔ .
Kết hợp m < 0 ta có
Kết hợp cả 2 trường hợp, ta thu được kết quả m ∈ .
Vậy m ∈ thỏa mãn yêu cầu bài toán.
Ta chọn phương án C.
Câu 4. Cho f(x) = mx2 – 2mx + m – 1. Giá trị nào của m để f(x) ≥ 0 vô nghiệm?
A. m ≤ 0;
B. m ≥ 0;
C. m < 0;
D. m > 0.
Hướng dẫn giải
Đáp án: C
Giải thích:
Nếu m = 0 ta có f(x) = –1 < 0 khi đó f(x) ≥ 0 vô nghiệm.
Do đó m = 0 thỏa mãn yêu cầu đề bài.
Nếu m ≠ 0 thì f(x) = mx2 – 2mx + m – 1 là tam thức bậc hai.
Ta có:
∆’ = (–m)2 – m.(m – 1)
= m2 – m2 + m
= m.
Ta có f(x) ≥ 0 vô nghiệm. Nghĩa là, f(x) < 0, với mọi giá trị của x.
⇔ a < 0 và ∆’ < 0
⇔ m < 0 và m < 0
⇔ m < 0.
Vậy m ≤ 0 thỏa mãn yêu cầu bài toán.
Ta chọn phương án A.
Câu 5. Cho f(x) = ax2 + bx + c (a ≠ 0) có đồ thị đi qua ba điểm (0; 1); (1; –2); (3; 5). Kết luận nào sau đây đúng?
A. f(x) âm trong khoảng ;
B. f(x) âm trong khoảng ;
C. f(x) âm trong khoảng (3; +∞);
D. f(x) dương trong khoảng .
Hướng dẫn giải
Đáp án: A
Giải thích:
Xét f(x) = ax2 + bx + c (a ≠ 0):
⦁ Ta có đồ thị đi qua điểm (0; 1) nên f(0) = 1.
Khi đó a.02 + b.0 + c = 1.
Vì vậy c = 1.
⦁ Ta có đồ thị đi qua điểm (1; –2) nên f(1) = –2.
Khi đó a.12 + b.1 + c = –2.
Vì vậy a + b + c = –2 (1)
Thế c = 1 vào (1) ta được a + b + 1 = –2.
Do đó a = –b – 3.
⦁ Ta có đồ thị đi qua điểm (3; 5) nên f(3) = 5.
Khi đó a.32 + b.3 + c = 5.
Vì vậy 9 a + 3b + c = 5 (2)
Thế c = 1 và a = –b – 3 vào (2) ta được 9(–b – 3) + 3b + 1 = 0.
Suy ra –9b – 27 + 3b + 1 = 0.
Do đó –6b – 26 = 0.
Vì vậy .
Với , ta có a = –b – 3 = > 0.
Vậy ta có tam thức bậc hai .
Ta có ∆ = > 0.
Suy ra f(x) có 2 nghiệm phân biệt là:
Ta có bảng xét dấu của f(x) như sau:
|
x |
–∞ 3 +∞ |
|
f(x) |
+ 0 – 0 + |
Vậy f(x) âm trong khoảng và f(x) dương trong hai khoảng và (3; +∞).
Ta chọn phương án A.