50 câu Trắc nghiệm Ôn tập Chương 1 (có đáp án 2024) – Toán 10 Chân trời sáng tạo
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Chương 1: Mệnh đề và tập hợp đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Chương 1.
Trắc nghiệm Toán 10 Ôn tập Chương 1
I. Nhận biết
Câu 1. Cho tập hợp A = {x ∈ ℝ | –3 < x < 1}. Tập A là tập nào sau đây?
A. {–3; 1};
B. [–3; 1];
C. [–3; 1);
D. (–3; 1).
Đáp án: D
Giải thích:
Ta thấy A là một tập con của tập số thực ℝ.
Do đó ta có thể dùng kí hiệu đoạn, khoảng, nửa khoảng để biểu diễn tập hợp A.
Ta thấy tập hợp A có dạng: {x ∈ ℝ | a < x < b}, với a = –3; b = 1.
Do đó ta có thể sử dụng kí hiệu khoảng (a; b) để biểu diễn tập hợp A.
Vậy ta có biểu diễn tập hợp A như sau: A = (–3; 1).
Ta chọn phương án D.
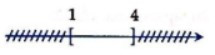
Câu 2. Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp (1; 4]?
A.
B.
C.
D.
Đáp án: A
Giải thích:
Tập hợp (1; 4] là tập hợp gồm các số thực sao cho 1 < x ≤ 4.
Tập hợp (1; 4] có dạng nửa khoảng (a; b], với a = 1, b = 4.
Do đó khi biểu diễn tập hợp (1; 4] trên trục số, ta thu được hình vẽ:
Vậy ta chọn phương án A.
Câu 3. Cho A = {1; 2; 4; 5} và B = {–2; –1; 0; 1; 2}. Khi đó A \ B là tập hợp:
A. {1; 2};
B. {–2; –1; 0; 1; 2; 4; 5};
C. {4; 5};
D. {–2; –1; 0}.
Đáp án: C
Giải thích:
Với A = {1; 2; 4; 5} và B = {–2; –1; 0; 1; 2}.
Khi đó A \ B là hiệu của tập hợp A và tập hợp B, gồm những phần tử thuộc A nhưng không thuộc B.
Þ A \ B = {4; 5}.
Ta chọn phương án C.
Câu 4. Cho các phát biểu sau:
(I) Mệnh đề P và mệnh đề phủ định 
của nó có tính đúng sai trái ngược nhau;
(II) Khi P đúng thì 
sai;
(III) Khi P sai thì 
sai.
Số các phát biểu đúng là:
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án: C
Giải thích:
Phát biểu (I) đúng.
Vì phát biểu (I) đúng nên ta có khi P đúng thì 
sai và khi P sai thì 
đúng.
Do đó phát biểu (II) đúng, phát biểu (III) sai.
Vậy có 2 phát biểu đúng là (I), (II).
Do đó ta chọn phương án C.
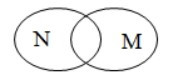
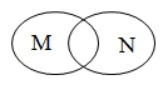
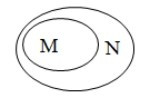
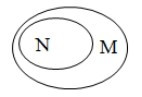
Câu 5. Cho hai tập hợp M và N. Hình nào sau đây minh họa M là tập con của N?
A.
B.
C.
D.
Đáp án: C
Giải thích:
Theo đề, ta có quan hệ bao hàm: M là tập con của N hay M ⊂ N.
Nên khi vẽ biểu đồ Ven, ta sẽ vẽ đường cong kín biểu diễn tập hợp M nằm gọn trong đường cong kín biểu diễn tập hợp N.
Ta thấy chỉ có biểu đồ ở phương án C thỏa mãn yêu cầu.
Do đó ta chọn phương án C.
Câu 6. Cho tập hợp P = {a; b; d}, Q = {a; b; c}. Tập P ∪ Q là tập hợp nào sau đây?
A. {a; b; c; d};
B. {a; b};
C. {c};
D. {a; b; c; d; e}.
Đáp án: A
Giải thích:
Tập P ∪ Q bao gồm các phần tử hoặc thuộc P, hoặc thuộc Q.
Các phần tử hoặc thuộc P, hoặc thuộc Q là: a; b; d; c.
Do đó tập P ∪ Q = {a; b; c; d}.
Vậy ta chọn phương án A.
Câu 7. Trong các câu sau, câu nào là mệnh đề?
A. Hôm nay là thứ mấy?
B. Các bạn làm bài đi!
C. Hôm nay trời rất đẹp.
D. Việt Nam là một nước thuộc châu Á.
Đáp án: D
Giải thích:
Phương án A: “Hôm nay là thứ mấy?” là câu hỏi, không khẳng định được tính đúng sai. Do đó đây không phải là một mệnh đề.
Phương án B: “Các bạn làm bài đi!” là câu cảm thán, không khẳng định được tính đúng sai. Do đó đây không phải là một mệnh đề.
Phương án C: “Hôm nay trời rất đẹp.” không khẳng định tính đúng sai do không đưa ra tiêu chí thế nào là trời rất đẹp. Do đó đây không phải là một mệnh đề.
Phương án D: “Việt Nam là một nước thuộc châu Á.” là một mệnh đề (mệnh đề đúng).
Vậy ta chọn phương án D.
Câu 8. Cho hai mệnh đề P và Q. Phát biểu mệnh đề P Û Q nào sau đây sai?
A. P khi và chỉ khi Q;
B. P tương đương Q;
C. P là điều kiện cần để có Q;
D. P là điều kiện cần và đủ để có Q.
Đáp án: C
Giải thích:
Mệnh đề P Û Q được phát biểu bằng một trong ba cách sau:
⦁ P khi và chỉ khi Q. Do đó phương án A đúng.
⦁ P tương đương Q. Do đó phương án B đúng.
⦁ P là điều kiện cần và đủ để có Q (hay Q là điều kiện cần và đủ để có P). Do đó phương án D đúng, phương án C sai.
Vậy ta chọn phương án C.
Câu 9. Cho hai tập hợp U = {1; 2; 3; 4}, V = {1; 2}. Tập CUV là tập hợp nào sau đây?
A. {1; 2};
B. {1; 2; 3; 4};
C. {3; 4};
D. ∅.
Đáp án: C
Giải thích:
Với U = {1; 2; 3; 4}, V = {1; 2} ta thấy V ⊂ U.
Tập CUV (= U \ V) bao gồm các phần tử thuộc U nhưng không thuộc V.
Các phần tử thuộc U nhưng không thuộc V là: 3; 4.
Do đó CUV = {3; 4}.
Vậy ta chọn phương án C.
Câu 10. Cho tập hợp X = {1; 5}, Y = {1; 3; 5}. Tập X ∩ Y là tập hợp nào sau đây?
A. {1};
B. {1; 3};
C. {1; 3; 5};
D. {1; 5}.
Đáp án: D
Giải thích:
Tập X ∩ Y là tập hợp gồm các phần tử vừa thuộc tập X, vừa thuộc tập Y.
Ta thấy 1; 5 là hai phần tử vừa thuộc tập X, vừa thuộc tập Y.
Do đó tập X ∩ Y = {1; 5}.
Vậy ta chọn đáp án D.
II. Thông hiểu
Câu 1. Cho mệnh đề chứa biến: P(x): “x + 15 ≤ x2” (x là số thực).
Mệnh đề nào sau đây đúng?
A. P(0);
B. P(5);
C. P(3);
D. P(4).
Đáp án: B
Giải thích:
Với x = 0, ta có P(0): “0 + 15 ≤ 02” là mệnh đề sai.
Với x = 5, ta có P(5): “5 + 15 ≤ 52” là mệnh đề đúng.
Với x = 3, ta có P(3): “3 + 15 ≤ 32” là mệnh đề sai.
Với x = 4, ta có P(4): “4 + 15 ≤ 42” là mệnh đề sai.
Vậy ta chọn phương án B.
Câu 2. Tính chất đặc trưng của tập hợp H = {1; 2; 3; 4; 5}.
A. {x ∈ ℕ | x ≤ 5};
B. {x ∈ 
| x ≤ 5};
C. {x ∈ ℤ | x ≤ 5};
D. {x ∈ ℝ | x ≤ 5}.
Đáp án: B
Giải thích:
⦁ Các phần tử của tập hợp ở phương án A là: {0; 1; 2; 3; 4; 5}.
Ta thấy phần tử 0 ∉ H.
Do đó tập hợp ở phương án A khác tập H.
⦁ Các phần tử của tập hợp ở phương án B là: {1; 2; 3; 4; 5} = H.
Do đó phương án B đúng.
⦁ Ta thấy phần tử –1 thuộc tập hợp ở đáp án C, D.
Nhưng –1 ∉ H.
Do đó tập hợp ở phương án C, D khác tập H.
Vậy ta chọn phương án B.
Câu 3. Cho tập hợp P = {1; 3} và tập hợp Q = {3; x}. Giá trị của x để P = Q là:
A. x = 1;
B. x = 2;
C. x = 3;
D. x = 5.
Đáp án: A
Giải thích:
Ta thấy tập hợp P và Q đều có phần tử 3.
Tập P còn có phần tử 1.
Do đó để P = Q thì Q cần có thêm phần tử 1.
Nghĩa là, x = 1.
Vậy ta chọn phương án A.
Câu 4. Mệnh đề “∃x ∈ ℝ: x2 = 4” khẳng định rằng:
A. Bình phương của mỗi số thực bằng 4;
B. Có ít nhất một số thực mà bình phương của nó bằng 4;
C. Chỉ có một số thực bình phương bằng 4;
D. Nếu x là một số thực thì x2 = 4.
Đáp án: B
Giải thích:
Mệnh đề “∃x ∈ ℝ: x2 = 4” có nghĩa là tồn tại (có ít nhất) một số thực x sao cho bình phương của nó bằng 4.
Do đó phương đáp án B đúng.
Phương án A sai vì kí hiệu trong mệnh đề là “∃” không phải “∀”.
Phương án C sai vì kí hiệu “∃” có nghĩa là “tồn tại” hay “có ít nhất”.
Phương án D sai vì mệnh đề “Nếu P thì Q” là mệnh đề kéo theo.
Vậy ta chọn phương án B.
Câu 5. Cho mệnh đề: “Nếu hai góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?
A. Nếu hai góc bằng nhau thì hai góc đó ở vị trí so le trong;
B. Nếu hai góc không ở vị trí so le trong thì hai góc đó không bằng nhau;
C. Nếu hai góc không bằng nhau thì hai góc đó không ở vị trí so le trong;
D. Nếu hai góc ở vị trí so le trong thì hai góc đó không bằng nhau.
Đáp án: A
Giải thích:
Trong mệnh đề: “Nếu hai góc ở vị trí so le trong thì hai góc đó bằng nhau”, ta thấy:
⦁ P: “Hai góc ở vị trí so le trong”;
⦁ Q: “Hai góc đó bằng nhau”.
Mệnh đề P Þ Q có mệnh đề đảo là mệnh đề Q Þ P.
Mệnh đề Q Þ P được phát biểu như sau: “Nếu hai góc bằng nhau, thì hai góc đó ở vị trí so le trong”.
Vậy ta chọn phương án A.
Câu 6. Viết tập hợp D gồm các chữ cái có trong từ “TOKYO”.
A. D = {T; O; K; Y; O};
B. D = {K; T; Y; O};
C. D = {T; O; Y};
D. D = {K; Y; T}.
Đáp án: B
Giải thích:
Các chữ cái trong từ “TOKYO” là: T; O; K; Y; O.
Do mỗi phần tử chỉ được liệt kê một lần nên ta có: T; O; K; Y.
Vậy tập hợp D ={T; O; K; Y}.
Do các phần tử có thể được viết theo thứ tự tùy ý.
Nên ta chỉ cần chọn tập hợp D ở phương án đã bao gồm đủ cả 4 phần tử T; O; K; Y.
Ta thấy đáp án B thỏa mãn yêu cầu.
Vậy ta chọn phương án B.
Câu 7. Cho tập hợp A = {x; y; z} và B = {x; y; z; t; u}. Tập hợp X nào trong các tập X dưới đây thỏa mãn A ⊂ X ⊂ B?
A. X = {x; y; z; t; u; v};
B. X = {x; y; z; t};
C. X = {y; t; u};
D. X = {t; u}.
Đáp án: B
Giải thích:
Tập A là tập con của tập B khi mọi phần tử của tập hợp A đều thuộc tập hợp B.
Ta thấy tập hợp A gồm 3 phần tử là: x; y; z.
Tập hợp B gồm 5 phần tử là: x; y; z; t; u.
Trong 4 phương án A, B, C, D, ta thấy tập X ở phương án A và B đều chứa cả 3 phần tử x; y; z, còn phương án C, D không chứa cả 3 phần tử x; y; z.
Nên ta loại phương án C, D.
Ta thấy tập X ở phương án A có phần tử v ∉ B.
Do đó tập X ở phương án A không phải tập con của tập B.
Ta thấy tập X ở phương án B có 4 phần tử là x; y; z; t đều thuộc tập B.
Do đó tập X ở phương án B là tập con của tập hợp B.
Vậy ta chọn đáp án B.
Câu 8. Phủ định của mệnh đề P: “∀x ∈ ℝ: x2 + 1 > 0” là:
A. 
: “∀x ∈ ℝ: x2 + 1 < 0”;
B. 
: “∃x ∈ ℝ: x2 + 1 ≤ 0”;
C. 
: “∃x ∈ ℝ: x2 + 1 > 0”;
D. 
: “∀x ∈ ℝ: x2 + 1 = 0”.
Đáp án: B
Giải thích:
Phủ định của ∀ là ∃.
Phủ định của x2 + 1 > 0 là x2 + 1 ≤ 0.
Vì vậy phủ định của mệnh đề: “∀x ∈ ℝ: x2 + 1 > 0” là “∃x ∈ ℝ: x2 + 1 ≤ 0”.
Vậy ta chọn phương án B.
Câu 9. Cho mệnh đề: “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”. Phát biểu mệnh đề trên bằng cách sử dụng thuật ngữ “điều kiện cần” là:
A. Tứ giác là hình thang cân là điều kiện cần để tứ giác đó có hai đường chéo bằng nhau;
B. Tứ giác có hai đường chéo bằng nhau là điều kiện cần để tứ giác đó là hình thang cân;
C. Nếu tứ giác không phải là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau;
D. Cả A, B, C đều sai.
Đáp án: B
Giải thích:
Trong mệnh đề P Þ Q: “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”, ta thấy:
⦁ P: “Một tứ giác là hình thang cân”;
⦁ Q: “Tứ giác có hai đường chéo bằng nhau”.
Do đó ta có phát biểu sau:
“Tứ giác có hai đường chéo bằng nhau là điều kiện cần để tứ giác đó là hình thang cân”.
Vậy ta chọn phương án A.
Câu 10. Khẳng định nào sau đây sai?
A. ℤ ∪ ℚ = ℚ;
B. ℕ ∪ ℕ* = ℕ*;
C. ℚ ∩ ℝ = ℚ;
D. ℕ* ∩ ℝ = ℕ*.
Đáp án: B
Giải thích:
Ta có quan hệ bao hàm: ℕ* Ì ℕ Ì ℤ Ì ℚ Ì ℝ.
Khi đó:
• ℤ ∪ ℚ = ℚ. Do đó A đúng;
• ℕ ∪ ℕ* = ℕ. Do đó B sai;
• ℚ ∩ ℝ = ℚ. Do đó C đúng;
• ℕ* ∩ ℝ = ℕ*. Do đó D đúng.
Vậy ta chọn phương án B.
Câu 11. Cho hai tập hợp G = (1; 5]; H = (2; 7]. Tập hợp G \ H là:
A. (1; 2];
B. (2; 5);
C. (–1; 7];
D. (–1; 2).
Đáp án: A
Giải thích:
Để xác định tập hợp G \ H, ta vẽ sơ đồ sau đây:
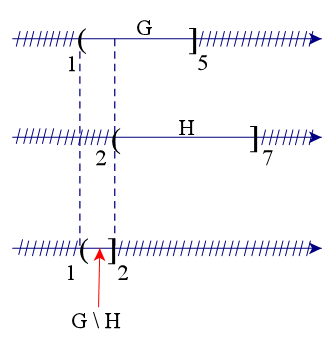
Từ sơ đồ, ta thấy G \ H = (1; 2] (vì tập H không lấy số 2 nên phần bù sẽ lấy số 2).
Vậy ta chọn phương án A.
Câu 12. Cho A, B, C là ba tập hợp được minh họa bằng biểu đồ Ven như hình vẽ.
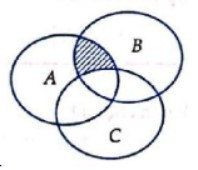
Phần gạch sọc trong hình vẽ là tập hợp nào sau đây?
A. (A ∪ B) \ C;
B. (A ∩ B) \ C;
C. (A \ C) ∪ (A \ B);
D. (A ∩ B) ∪ C.
Đáp án: B
Giải thích:
Quan sát hình vẽ, ta thấy mỗi phần tử x thuộc phần gạch sọc đều thỏa mãn cả 3 yêu cầu sau:
⦁ x ∈ A;
⦁ x ∈ B;
⦁ x ∉ C.
Vì x ∈ A và x ∈ B nên ta có x ∈ (A ∩ B).
Vì x ∈ (A ∩ B) và x ∉ C nên ta có x ∈ (A ∩ B) \ C.
Vậy ta chọn phương án B.
Câu 13. Cho A: “Tập hợp các học sinh khối 10 học giỏi”, B: “Tập hợp các học sinh nữ khối 10 học giỏi”, C: “Tập hợp các học sinh nam khối 10 học giỏi”. Vậy tập hợp C là:
A. A ⊂ B;
B. B \ A;
C. A ∩ B;
D. A \ B.
Đáp án: D
Giải thích:
Vì tập hợp B là tập hợp các học sinh nữ khối 10 học giỏi nên tập hợp C gồm những phần tử thuộc tập hợp A mà không thuộc tập hợp B.
Do đó C = A \ B.
Ta chọn phương án D.
Câu 14. Cho tập hợp A = (–∞;–2] và tập B = (–1; +∞). Khi đó A ∪ B là:
A. (–2; +∞);
B. (–2; –1];
C. ℝ;
D. ∅.
Đáp án: C
Giải thích:
Để xác định tập hợp A ∪ B, ta vẽ sơ đồ sau đây:
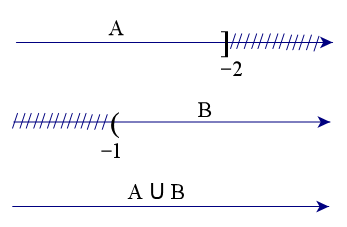
Từ sơ đồ, ta thấy A ∪ B = ℝ.
Vậy ta chọn phương án C.
Câu 15. Cho tập hợp C = [–5; 3), D = (1; +∞). Khi đó C ∩ D là tập nào sau đây?
A. (1; 3);
B. (1; 3];
C. [–5; +∞);
D. [–5; 1].
Đáp án: A
Giải thích:
Để xác định tập hợp C ∩ D, ta vẽ sơ đồ sau đây:
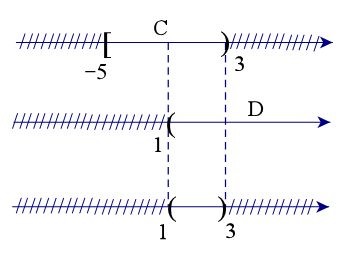
Từ sơ đồ, ta thấy C ∩ D = (1; 3).
Vậy ta chọn phương án A.
III. Vận dụng
Câu 1. Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh?
A. 54;
B. 40;
C. 26;
D. 68.
Đáp án: B
Giải thích:
Gọi T, L, K lần lượt là tập hợp các học sinh giỏi Toán, tập hợp các học sinh giỏi Lý và tập học các học sinh không giỏi môn nào cả.
Theo đề, ta có:
⦁ n(T) = 25;
⦁ n(L) = 23;
⦁ n(T ∩ L) = 14;
⦁ n(K) = 6.
Ta có sơ đồ Ven biểu diễn 3 tập hợp T, L, K như sau:
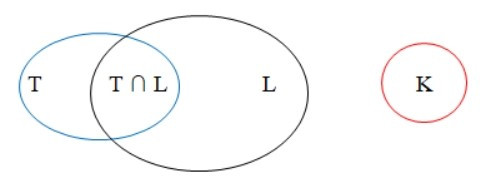
Khi đó số học sinh cả lớp là: n(T ∪ L) + n(K).
Ta có n(T ∪ L) = n(T) + n(L) – n(T ∩ L) = 25 + 23 – 14 = 34.
Vậy số học sinh cả lớp là: 34 + 6 = 40 (học sinh).
Do đó ta chọn phương án B.
Câu 2. Mệnh đề nào sau đây là sai?
A. Phương trình x2 + bx + c = 0 có nghiệm Û b2 – 4c ≥ 0;
B.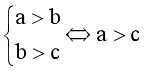 
;
C. ∆ABC vuông tại A Û 
;
D. π < 4 Û π2 < 16.
Đáp án: B
Giải thích:
⦁ Phương trình x2 + bx + c = 0 có nghiệm Û ∆ ≥ 0.
Û b2 – 4c ≥ 0.
Do đó phương án A đúng.
⦁ Nếu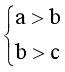 
(hay a > b > c) thì a > c.
Do đó mệnh đề P Þ Q đúng (1)
Ta xét mệnh đề đảo Q Þ P: a > c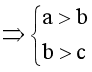 
.
Ta chọn a, b, c sao cho Q đúng.
Chọn a = 4; c = 2; b = 1.
Vì 4 > 2 nên ta suy ra a > c, tức là Q đúng.
Khi đó ta có 4 > 2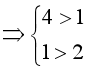 
.
Lúc này P vô lý vì 1 < 2.
Do đó Q đúng và P sai.
Vì vậy mệnh đề đảo Q Þ P sai (2)
Từ (1), (2), ta suy ra phương án B sai.
Đến đây ta có thể chọn phương án B.
⦁ Nếu ∆ABC vuông tại A thì 
.
∆ABC có: 
(định lí tổng ba góc trong một tam giác).
Suy ra 
.
Vì vậy mệnh đề P Þ Q đúng (3)
Nếu 
thì:
∆ABC có: 
(định lí tổng ba góc trong một tam giác).
Suy ra 
.
Do đó ∆ABC vuông tại A.
Vì vậy mệnh đề Q Þ P đúng (4)
Từ (1), (2), ta suy ra P Û Q.
Do đó phương án C đúng.
⦁ Ta có π ≈ 3,14 < 4.
Suy ra π2 ≈ 9,87 < 16.
Do đó P Þ Q đúng (5)
Ngược lại, ta có π2 ≈ 9,87 < 16.
Suy ra π ≈ 3,14 < 4.
Do đó Q Þ P đúng (6)
Từ (5), (6), ta suy ra P Û Q.
Do đó phương án D đúng.
Vậy ta chọn phương án B.
Câu 3. Cho tập A có n + 1 phần tử (n ∈ ℕ*). Số tập con của A có hai phần tử là:
A. n(n + 1);
B.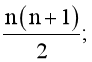 
C. n + 1;
D.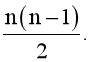 
Đáp án: B
Giải thích:
Lấy một phần tử của A ghép với n phần tử còn lại ta được n tập con có hai phần tử.
Vậy có (n + 1).n tập.
Nhưng mỗi tập con đó được tính hai lần do được lặp lại nên số tập con của A có hai phần tử là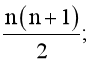 
Vậy ta chọn phương án B.
Câu 4. Cho ba tập hợp A = [–2; 2], B = [1; 5], C = [0; 1]. Khi đó tập (A \ B) ∩ C là:
A. {0; 1};
B. [0; 1);
C. (–2; 1);
D. [–2; 5].
Đáp án: B
Giải thích:
Để xác định tập hợp A \ B, ta vẽ sơ đồ sau đây:
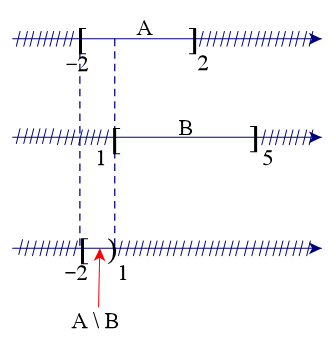
Từ sơ đồ, ta thấy A \ B = [–2; 1) (vì tập B chứa số 1 nên phần bù sẽ không lấy số 1).
Để xác định tập hợp (A \ B) ∩ C, ta vẽ sơ đồ sau đây:
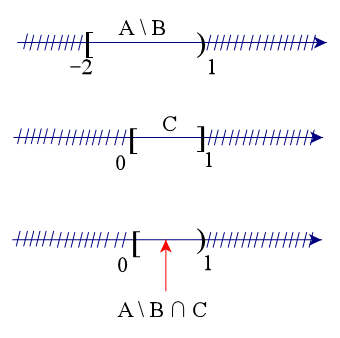
Từ sơ đồ, ta thấy (A \ B) ∩ C = [0; 1) (giao tức là lấy phần chung, tuy tập C có số 1 nhưng vì tập A \ B không lấy số 1 nên ta không lấy số 1).
Vậy ta chọn phương án B.
Câu 5. Cho hai tập khác rỗng A = (m – 1; 4], B = (–2; 2m + 2), m ∈ ℝ. Tìm m để A ∩ B ≠ ∅.
A. –1 < m < 5;
B. 1 < m < 5;
C. –2 < m < 5;
D. m > –3.
Đáp án: C
Giải thích:
Vì tập A khác rỗng nên ta có m – 1 < 4.
Û m < 5 (1)
Vì tập B khác rỗng nên ta có –2 < 2m + 2.
Û –4 < 2m.
Û m > –2 (2)
Từ (1) và (2), ta suy ra tập hợp A và B đều khác rỗng khi và chỉ khi –2 < m < 5 (*).
Để A ∩ B ≠ ∅ thì m – 1 < 2m + 2.
Nghĩa là, m > –3 (**).
Giao (*) và (**) lại với nhau, ta thu được kết quả –2 < m < 5.
Vậy ta chọn phương án C.