50 câu Trắc nghiệm Toạ độ của vectơ (có đáp án 2024) – Toán 10 Chân trời sáng tạo
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 1: Toạ độ của vectơ đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 1.
Trắc nghiệm Toán 10 Bài 1: Toạ độ của vectơ
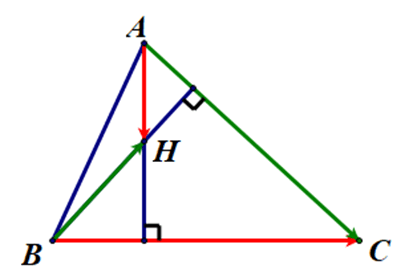
Câu 1. Trong mặt phẳng Oxy, cho ∆ABC có A(–3; 0), B(3; 0) và C(2; 6). Gọi H(a; b) là trực tâm của ∆ABC. Giá trị của a + 6b bằng:
A. 3;
B. 6;
C. 7;
D. 5.
Đáp án đúng là: C
+ Với A(–3; 0), B(3; 0), C(2; 6) và H(a; b) ta có:
• →BC=(−1;6),→AC=(5;6).
• →AH=(a+3;b),→BH=(a−3;b).
+ Vì H là trực tâm của ∆ABC nên AH ⊥ BC.
Suy ra →AH⊥→BC.
Do đó →AH.→BC=0
Khi đó ta có (a + 3).(–1) + 6b = 0
Vì vậy –a + 6b – 3 = 0 (1).
+ Vì H là trực tâm của ∆ABC nên BH ⊥ AC.
Suy ra →BH⊥→AC
Do đó →BH.→AC=0
Khi đó ta có (a – 3).5 + 6b = 0
Vì vậy 5a + 6b – 15 = 0 (2).
Từ (1) và (2), ta có hệ phương trình:
(−a+6b−3=05a+6b−15=0)⇔(a=2b=56)
Do đó ta có a + 6b = 2 + 6.56 = 7.
Vậy ta chọn phương án C.
Câu 2. Cho mặt phẳng Oxy, cho ∆ABC có G là trọng tâm. Biết B(4; 1), C(1; –2) và G(2; 1). Tọa độ điểm A là:
A. A(1; 4);
B. A(3; 0);
C. A(4; 1);
D. A(0; 3).
Đáp án đúng là: A
Vì G là trọng tâm của ∆ABC nên ta có: (xG=xA+xB+xC3yG=yA+yB+yC3)
⇔(3xG=xA+xB+xC3yG=yA+yB+yC)⇔(xA=3xG−xB−xCyA=3yG−yB−yC)⇔(xA=3.2−4−1=1yA=3.1−1−(−2)=4)
Do đó ta được A(1; 4).
Vậy ta chọn phương án A.
Câu 3. Trong mặt phẳng Oxy, cho ba điểm A(–2; –3), B(1; 4) và C(3; 1). Đặt →u=→AB+→AC. Tọa độ của là:
A. (–2; 3);
B. (–8; –11);
C. (2; –3);
D. (8; 11).
Đáp án đúng là: D
Với A(–2; –3), B(1; 4) và C(3; 1) ta có:
+) →AB=(xB−xA;yB−yA)=(1−(−2);4−(−3))=(3;7).
+) →AC=(xC−xA;yC−yA)=(3−(−2);1−(−3))=(5;4).
Do đó ta được →u=→AB+→AC=(3+5;7+4)=(8;11).
Vậy ta chọn phương án D.
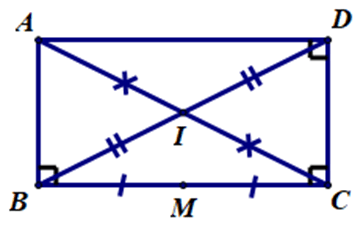
Câu 4. Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có A(0; 3), D(2; 1) và I(–1; 0) là tâm của hình chữ nhật. Tọa độ trung điểm của đoạn thẳng BC là:
A. (–3; –2);
B. (–2; 1);
C. (4; –1);
D. (1; 2).
Đáp án đúng là: A
Gọi M(x; y) là trung điểm của đoạn thẳng BC.
Vì I là tâm của hình chữ nhật ABCD nên I là trung điểm AC.
Suy ra (xI=xA+xC2yI=yA+yC2)
⇔(2xI=xA+xC2yI=yA+yC) ⇔(xC=2xI−xAyC=2yI−yA) ⇔(xC=2.(−1)−0=−2yC=2.0−3=−3)
Suy ra tọa độ C(–2; –3).
Tương tự, ta được B(–4; –1).
Vì M(x; y) là trung điểm đoạn thẳng BC.
Nên (xM=xB+xC2=−4−22=−3yM=yB+yC2=−1−32=−2)
Do đó tọa độ M(–3; –2).
Vậy ta chọn phương án A.
Câu 5. Cho →a=(1;2), →b=(−2;3). Góc giữa hai vectơ →u=3→a+2→b và →v=→a−5→b bằng
A. 45°;
B. 60°;
C. 90°;
D. 135°.
Đáp án đúng là: D
Với →a=(1;2), →b=(−2;3) ta có:
+) 3→a=(3.1;3.2)=(3;6), 2→b=(2.(−2);2.3)=(−4;6).
Suy ra →u=3→a+2→b=(3−4;6+6)=(−1;12).
+) →a=(3;4), 5→b=(5.(−2);5.3)=(−10;15).
Suy ra →v=→a−5→b=(3−(−10);4−15)=(13;−11).
Ta có: cos(→u,→v)=→u.→v(→u).(→v)
=−1.13+12.(−11)√(−1)2+122.√132+(−11)2
=−145√145.√290=−1√2
Suy ra (→u,→v)=135°.
Câu 6. Trong mặt phẳng Oxy, cho ba điểm A(1; 5), B(–1; 0) và C(1; 3). M là điểm nằm trên trục Oy sao cho cùng phương với . Tọa độ điểm M là:
A.
B.
C.
D.
Đáp án đúng là: D
Vì M thuộc trục Oy nên M(0; y).
Với A(1; 5), B(–1; 0), C(1; 3) và M(0; y) ta có:
+) .
+) .
Theo đề, ta có cùng phương với
⇔ –1.3 – (y – 5).2 = 0
⇔ –3 – 2y + 10 = 0
⇔ –2y + 7 = 0
⇔ y =
Vậy
Do đó ta chọn phương án D.
Câu 7. Trong mặt phẳng Oxy, cho hai điểm A(1; 2) và B(–2; 3). Gọi B’ là điểm đối xứng của B qua A. Tọa độ điểm B’ là:
A. B’(4; 1);
B. B’(0; 1);
C. B’(–4; –1);
D. B’(0; –1).
Đáp án đúng là: A
Vì B’ là điểm đối xứng của B qua A nên ta có A là trung điểm của BB’.
Suy ra
Do đó B’(4; 1).
Vậy ta chọn phương án A.
Câu 8. Trong mặt phẳng Oxy, cho hai điểm A(1; 2) và B(–1; 5). Tìm m để điểm C(2; m) thuộc đường thẳng AB.
A. m = 1;
B. ;
C. ;
D. m = 2.
Đáp án đúng là: B
Với A(1; 2) và B(–1; 5) và C(2; m) ta có:
.
.
Theo đề, ta có điểm C(2; m) thuộc đường thẳng AB.
Tức là cùng phương ⇔ –2.(m – 2) – 1.3 = 0
⇔ –2m + 4 – 3 = 0
⇔ –2m + 1 = 0
⇔ –2m = –1
Vậy ta chọn phương án B.
Câu 9. Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng là:
A. x ∈∅;
B. x = 1;
C. x = 11;
D. x = 11 hoặc x = 1.
Đáp án đúng là: D
Ta có
Suy ra
Theo đề, ta có AB = .
⇔ x2 – 12x + 36 + 100 = 125
⇔ x2 – 12x + 11 = 0
⇔ x = 11 hoặc x = 1.
Vậy ta chọn phương án D.
Câu 10. Cho và . Tìm a để .
A. ;
B. ;
C. ;
D. .
Đáp án đúng là: B
Ta có
⇔ 4.3 + 5.a = 0
⇔ 12 + 5a = 0
⇔ 5a = –12
Vậy ta chọn phương án B.
Câu 11. Trong mặt phẳng Oxy, cho và . Kết luận nào sau đây sai?
A. ;
B. ;
C. ;
D. .
Đáp án đúng là: C
Ta có:
+)
+) .
•Ta xét phươngán A:
Ta có (đúng).
Do đó phươngán A đúng.
•Ta xét phươngán B:
Từ phươngán A, ta có .
Do đó phươngán B đúng.
•Ta xét phươngán C:
Ta có .
Do đó phươngán C sai.
Đến đây ta có thể chọn phươngán C.
•Ta xét phươngán D:
Từ phươngán A, ta có .
Do đó phươngán D đúng.
Vậy ta chọn phương án C.
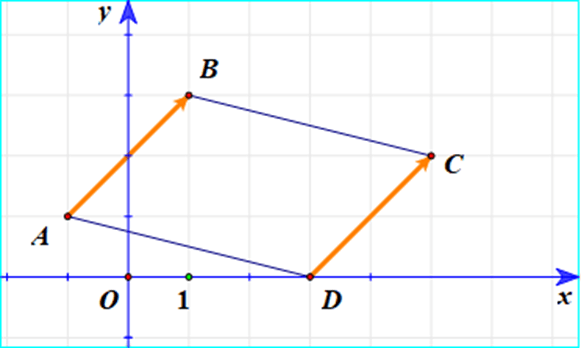
Câu 12. Trong mặt phẳng Oxy, cho ba điểm A(–1; 1), B(1; 3), C(5; 2). Tọa độ điểm D là đỉnh thứ tư của hình bình hành ABCD là:
A. (3; –2);
B. (5; 0);
C. (3; 0);
D. (5; –2).
Đáp án đúng là: C
Với A(–1; 1), B(1; 3), C(5; 2) và D(xD; yD) ta có:
+) .
+) .
Tứ giác ABCD là hình bình hành ⇔ .
.
Ta suy ra tọa độ D(3; 0).
Vậy ta chọn phương án C.
Câu 13. Trong mặt phẳng Oxy, cho , . Tìm x để và cùng phương.
A. x = –5;
B. x = 4;
C. x = 0;
D. x = –1.
Đáp án đúng là: C
Ta có và cùng phương ⇔ –5.x – 0.4 = 0
⇔ –5x = 0
⇔ x = 0.
Vậy ta chọn phương án C.
Câu 14. Trong mặt phẳng Oxy, cho , . Tìm tọa độ của sao cho .
A. ;
B. ;
C. ;
D. .
Đáp án đúng là: A
Từ suy ra .
Ta có .
Vậy ta chọn phương án A.
Câu 15. Trong mặt phẳng Oxy, cho và . Tính .
A. 6;
B. 2;
C. 4;
D. –4.
Đáp án đúng là: C
Ta có:
+) .
+) .
Suy ra .
Vậy ta chọn phương án C.