50 câu Trắc nghiệm Ba đường conic trong mặt phẳng toạ độ (có đáp án 2024) – Toán 10 Chân trời sáng tạo
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 4: Ba đường conic trong mặt phẳng toạ độ đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 4.
Trắc nghiệm Toán 10 Bài 4: Ba đường conic trong mặt phẳng toạ độ
Câu 1. Cho hypebol (H): 4x2 – y2 = 1. Khẳng định nào sau đây đúng?
A. Hypebol có tiêu cự bằng √52;
B. Hypebol có một tiêu điểm là F(√5;0);
C. Hypebol có trục thực bằng 1;
D. Hypebol có trục ảo bằng 12.
Đáp án đúng là: C
Ta có 4x2 – y2 = 1.
Suy ra x214−y21=1
Hay x2(12)2−y212=1.
Khi đó ta có a = 12, b = 1.
• Ta có b=√c2−a2
Suy ra c=√b2+a2=√1+14=√52.
Vậy hypebol (H) có tiêu cự là 2c = √5≠√52.
Do đó phương án A sai.
•Ta có c=√52.
Suy ra hai tiêu điểm của (H) là F1(−√52;0),F2(√52;0).
Do đó phương án B sai.
•Ta có trục thực là: A1A2 = 2a = 2.12 = 1.
Do đó phương án C đúng.
•Ta có trục ảo là: 2b = 2.1 = 2 ≠ 12.
Do đó phương án D sai.
Vậy ta chọn phương án C.
Câu 2. Cho parabol (P): y2 = 16x. Khẳng định nào sau đây sai?
A. (P) có tiêu điểm F(4; 0);
B. (P) có tọa độ đỉnh O(0; 0);
C. Phương trình đường chuẩn ∆: x = 4;
D. (P) nhận Ox làm trục đối xứng.
Đáp án đúng là: C
•Ta có (P): y2 = 16x nên 2p = 16.
Suy ra p = 8.
Do đó p2=82=4.
Vì vậy (P) có tiêu điểm F(4; 0).
Do đó phương án A đúng.
• Ta có O(0; 0) là đỉnh của parabol (P) và Ox là trục đối xứng của parabol (P).
Do đó phương án B, D đúng.
Đến đây ta có thể chọn đáp án C.
• Phương trình đường chuẩn ∆ có dạng: x=−p2=−4.
Do đó phương án C sai.
Vậy ta chọn phương án C.
Câu 3. Elip có tỉ số giữa độ dài trục nhỏ và tiêu cự bằng √2, tổng bình phương độ dài trục lớn và tiêu cự bằng 64. Phương trình chính tắc của elip là:
A. x212+y28=1;
B. x28+y212=1;
C. x212+y24=1;
D. x28+y24=1.
Đáp án đúng là: A
Ta có tỉ số giữa độ dài trục nhỏ và tiêu cự bằng √2.
Suy ra 2b2c=√2
⇔b=c√2
⇔√a2−c2=c√2
⇔ a2 – c2 = 2c2
⇔ a2 = 3c2.
Lại có tổng bình phương độ dài trục lớn và tiêu cự bằng 64.
Ta suy ra (2a)2 + (2c)2 = 64.
⇔ 4a2 + 4c2 = 64.
⇔ a2 + c2 = 16.
⇔ 3c2 + c2 = 16.
⇔ 4c2 = 16.
⇔ c2 = 4.
⇔ c = 2 (vì c > 0).
Với c = 2, ta có:
• a2 = 3c2 = 3.22 = 12.
•b = c√2=2√2.
Suy ra b2 = 8.
Vậy phương trình elip cần tìm là: x212+y28=1.
Do đó ta chọn phương án A.
Câu 4. Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường parabol?
A. x28+y224=1;
B. y2 = 2x;
C. x264−y249=1;
D. x2 = 21y.
Đáp án đúng là: B
Phương trình parabol có dạng: y2 = 2px.
Ta thấy chỉ có phương trình của đáp án B có dạng phương trình parabol trên.
Vậy ta chọn phương án B.
Câu 5. Cho elip (E): x2169+y2144=1. Nếu điểm M nằm trên (E) có hoành độ bằng –13 thì độ dài MF1 và MF2 lần lượt là:
A. 10 và 6;
B. 8 và 18;
C. 13±√5;
D. 13±√10.
Đáp án đúng là: B
Phương trình elip (E) có dạng: x2a2+y2b2=1, với a = 13, b = 12.
Ta có c=√a2−b2=√169−144=5.
Khi đó F1(–5; 0) và F2(5; 0).
Với M(xM; yM) ta có:
→F1M=(xM+5;yM) nên F1M=√(xM+5)2+y2M
F1M=√(xM+5)2+144.(1−x2M169)
F1M=√169+10xM+25169x2M
F1M=√(13+513xM)2
F1M=13+513xM (do F1M > 0).
Tương tự ta có F2M=13−513xM
Mà theo bài xM = –13 nên ta có:
• MF1 = 13+513.(−13)=8.
• MF2 = 13−513.(−13)=18.
Do đó ta chọn phương án B.
Câu 6. Cho hypebol (H): x236−y29=1. Tỉ số giữa độ dài trục ảo và độ dài trục thực bằng:
A. 2;
B. 12;
C. √52;
D. 2√55.
Đáp án đúng là: B
(H): x236−y29=1.
Ta có a = 6, b = 3.
Suy ra:
⦁ Độ dài trục ảo là: 2.3 = 6;
⦁ Độ dài trục thực là: 2.6 = 12.
Khi đó tỉ số giữa độ dài trục ảo và độ dài trục thực 2b2a=612=12.
Vậy ta chọn phương án B.
Câu 7. Cho hypebol (H): x24−y24=1. Tỉ số giữa tiêu cự và độ dài trục thực bằng:
A. 1;
B. √22;
C. √24;
D. √2.
Đáp án đúng là: D
(H): x24−y24=1 nênta có a = b = 2.
Suy ra c=√a2+b2=√4+4=2√2.
Khi đó ta có:
⦁ Tiêu cự là: 2c = 2.2√2=4√2;
⦁ Độ dài trục thực là: 2a = 2.2 = 4.
Khi đó 2c2a=4√24=√2.
Vậy ta chọn phương án D.
Câu 8. Cho điểm M(5; 8) nằm trên parabol (P): y2=645x. Độ dài FM bằng:
A. 4110;
B. 415;
C. 515;
D. 575.
Đáp án đúng là: B
Ta có 2p=645.
Suy ra p=325.
Do đó p2=165
Khi đó ta có tiêu điểm F(165;0).
Với F(165;0) và M(5; 8) ta có →FM=(95;8).
Suy ra FM=√(95)2+82=415.
Vậy ta chọn phương án B.
Câu 9. Bác An dự định xây một cái ao hình elip ở giữa khu vườn. Biết trục lớn có độ dài bằng 4 m, độ dài trục nhỏ bằng 2 m. Gọi F1, F2 là các tiêu điểm của elip. Khi đó độ dài F1F2 bằng:
A. 2√3;
B. √3;
C. √5;
D. 2√5.
Đáp án đúng là: A
Ta có độ dài trục lớn bằng 4 m. Suy ra 2a = 4.
Khi đó a = 2.
Lại có độ dài trục nhỏ bằng 2m. Suy ra 2b = 2.
Khi đó b = 1.
Ta có c2 = a2 – b2 = 22 – 12 = 3.
Suy ra c=√3.
Vì vậy F1F2 = 2c = 2√3.
Vậy ta chọn phương án A.
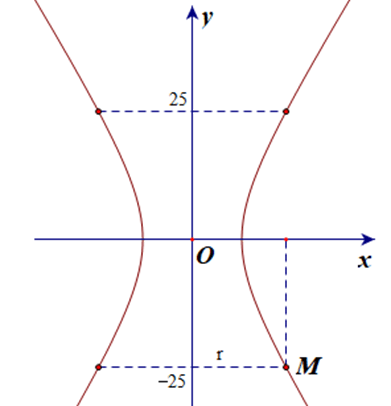
Câu 10.Một tòa tháp có mặt cắt hình hypebol có phương trình x236−y249=1. Biết khoảng cách từ nóc tháp đến tâm đối xứng O của hypebol bằng khoảng cách từ tâm đối xứng O đến đáy tháp. Tòa tháp có chiều cao 50 m. Bán kính đáy của tháp bằng:
A. 43,28 m;
B. 22,25 m;
C. 28,31 m;
D. 57,91 m.
Đáp án đúng là: B
Gọi r là bán kính đáy của tháp (r > 0).
Do tính đối xứng của hypebol nên ta có hai bán kính của nóc và đáy tháp đều bằng nhau.
Chọn điểm M(r; –25) nằm trên hypebol.
Ta suy ra r236−(−25)249=1.
⇔r236=1+(−25)249=67449.
⇔r2=67449.36=2426449.
Suy ra r=6√6747≈22,25 (m).
Vậy bán kính đáy của tháp bằng khoảng 22,25 m.
Do đó ta chọn phương án B.
Câu 11. Cho parabol (P) có đường chuẩn là đường thẳng ∆: x + 5 = 0. Điểm M thuộc (P) sao cho khoảng cách từ M đến tiêu điểm của parabol (P) bằng 6. Tọa độ điểm M là:
A. M(1;−2√5); M(1;−2√5) ;
B. M(1;2√5);
C. M(−1;−2√5);
D. M(−1;2√5); M(−1;−2√5) .
Đáp án đúng là: A
Phương trình đường chuẩn ∆: x + 5 = 0
Do đó ta có p2=5.
Suy ra p = 10.
Từ đó ta thu được phương trình parabol (P): y2 = 20x.
Tiêu điểm F của (P) là F(5; 0).
Giả sử điểm M(xM; yM) là điểm thuộc (P).
Khi đó y2M = 20xM
Với F(5; 0) và M(xM; yM) ta có →FM=(xM−5;yM)
⇒ FM=√(xM−5)2+y2M
FM=√x2M−10xM+25+20xM
FM=√x2M+10xM+25
FM=√(xM+5)2=xM+5
Theo đề, ta có FM = 6.
⇔ xM + 5 = 6
⇔ xM = 1.
Với xM = 1, ta có y2M = 20.1 = 20.
Suy ra yM=2√5 hoặc yM=−2√5
Vậy M(1;2√5) và M(1;−2√5) thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án A.
Câu 12. Cho điểm A(3; 4) thuộc parabol (P). Phương trình chính tắc của parabol (P) là:
A. y2=316x;
B. y2=163x;
C. y2=83x;
D. y2=23x.
Đáp án đúng là: B
Phương trình chính tắc của parabol (P) có dạng: y2 = 2px.
Ta có A(3; 4) ∈ (P).
Suy ra 42 = 2.p.3
Do đó 16 = 6p
Khi đó ta có p=83 suy ra 2p = 163
Vậy phương trình chính tắc của parabol (P): y2=163x.
Do đó ta chọn phương án B.
Câu 13. Cho elip (E): x225+y29=1. Trong các khẳng định sau, khẳng định nào sai?
A. (E) có các tiêu điểm F1(–4; 0) và F2(4; 0);
B. (E) có tỉ số ca=45;
C. (E) có đỉnh A1(–5; 0);
D. (E) có độ dài trục nhỏ bằng 3.
Đáp án đúng là: D
•Phương trình elip (E) có dạng: x2a2+y2b2=1, với a2 = 25, b2 = 9.
Ta suy ra a = 5, b = 3 (vì a, b > 0).
Ta có b = √a2−c2
⇔ b2 = a2 – c2
⇔ c2 = a2 – b2 = 25 – 9 = 16.
⇔ c = 4.
Vậy các tiêu điểm của elip (E) là: F1(–4; 0), F2(4; 0).
Do đó phương án A đúng.
• Ta có tỉ số ca=45.
Do đó phương án B đúng.
•Đỉnh A1(–a; 0).
Suy ra A1(–5; 0).
Do đó phương án C đúng.
• Độ dài trục nhỏ là 2b = 2.3 = 6 ≠ 3.
Do đó phương án D sai.
Vậy ta chọn phương án D.
Câu 14. Hypebol có độ dài trục thực gấp đôi độ dài trục ảo và có tiêu cự bằng 4√15. Phương trình chính tắc của hypebol là:
A. x248−y212=1;
B. x212−y248=1;
C. x248+y212=1;
D. x248+y212=1.
Đáp án đúng là: A
Theo đề, ta có độ dài trục thực gấp đôi độ dài trục ảo
Ta suy ra 2a = 2.2b.
Do đó a = 2b.
Hypebol có tiêu cự bằng 4√15.
Ta suy ra 2c=4√15.
Do đó c=2√15.
⇔√a2+b2=2√15
⇔ 4b2 + b2 = 60.
⇔ 5b2 = 60.
⇔ b2 = 12.
⇔b=2√3.
Với b=2√3, ta có: a=2b=4√3.
Suy ra a2 = 48.
Vậy ta có phương trình chính tắc của hypebol là:
x248−y212=1.
Do đó ta chọn phương án A.
Câu 15. Một anten gương đơn hình parabol có phương trình y2 = 20x. Ống thu của anten được đặt tại tiêu điểm của nó. Ta sẽ đặt ống thu tại điểm có tọa độ là:
A. (0; 10);
B. (0 ; 5);
C. (10; 0);
D. (5; 0).
Đáp án đúng là: D
Phương trình parabol có dạng y2 = 2px, với p = 10.
Suy ra p2=102=5.
Khi đó tọa độ tiêu điểm F(5; 0).
Vậy ta sẽ đặt ống thu tại điểm có tọa độ (5; 0).
Do đó ta chọn phương án D.