50 câu Trắc nghiệm Xác suất của biến cố (có đáp án 2024) – Toán 10 Chân trời sáng tạo

Đáp án: D

Giải thích:

Gọi biến cố A: “Có ít nhất 2 lần lấy viên bi cùng màu ”.

Ta kí hiệu X, Đ, T lần lượt để chỉ các viên bi màu xanh, màu đỏ, màu trắng.

Các kết quả có thể xảy ra trong 3 lần lấy ngẫu nhiên một viên bi được thể hiện ở sơ đồ hình cây sau:

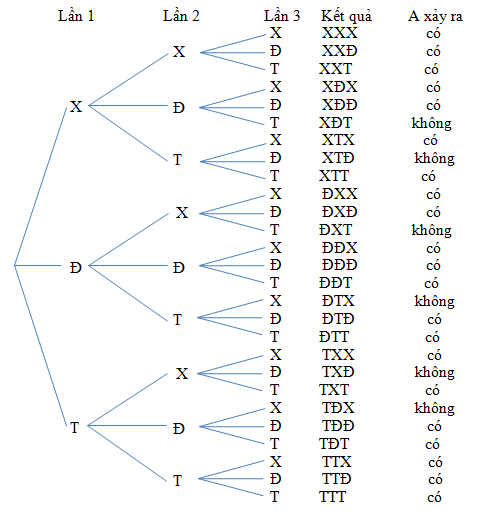
Quan sát sơ đồ hình cây, ta thấy có tổng cộng là 27 kết quả. Tức là, n(Ω) = 27.

Trong đó có 21 kết quả thuận lợi cho biến cố A. Tức là, n(A) = 21.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{21}{27}=\frac{3}{4}$.

Ta chọn phương án D.

Đáp án: C

Giải thích:

Số phần tử của không gian mẫu là: n(Ω) = 5! = 120.

Gọi biến cố A: “Số tìm được không có dạng $\overline{135xy}$ ”.

Suy ra biến cố đối của biến cố A là: $\overline{A}$: “Số tìm được có dạng $\overline{135xy}$”.

⦁ x có 2 cách chọn là x = 7 hoặc x = 9.

⦁ y có 1 cách chọn.

Theo quy tắc đếm, ta có $n\left(\overline{A}\right)$ = 1.1.1.2.1 = 2 cách chọn.

Vì vậy xác suất của biến cố $\overline{A}$ là: $P\left(\overline{A}\right)=\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{2}{120}=\frac{1}{60}$.

Ta có $P\left(A\right)+P\left(\overline{A}\right)=1$.

Suy ra $P\left(A\right)=1-P\left(\overline{A}\right)=1-\frac{1}{60}=\frac{59}{60}$.

Vậy ta chọn phương án C.

Đáp án: B

Giải thích:

Có tất cả 15 + 6 = 21 người trong hội nghị.

Chọn ngẫu nhiên 3 trong số 21 người và không tính đến thứ tự thì có $C_{21}^3=1330$ cách chọn.

Tức là n(Ω) = 1 330.

Gọi biến cố A: “3 người được chọn là nam”.

Chọn ngẫu nhiên 3 nam trong số 15 nam và không tính đến thứ tự thì có $C_{15}^3=455$ cách chọn.

Tức là n(A) = 455.

Vậy xác suất để 3 người được chọn là nam là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{455}{1330}=\frac{13}{38}$.

Ta chọn phương án B.

Đáp án: C

Giải thích:

Số phần tử của không gian mẫu là: n(Ω) = 6.6 = 36.

Gọi biến cố A: “Hiệu số chấm các mặt xuất hiện của hai xúc xắc bằng 2”.

Suy ra tập hợp biến cố A là:

A = {(1; 3), (3; 1), (2; 4), (4; 2), (3; 5), (5; 3), (4; 6), (6; 4)}.

Do đó n(A) = 8.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{8}{36}=\frac{2}{9}$.

Ta chọn phương án C.

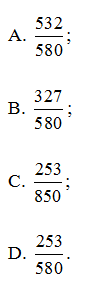
Đáp án: D

Giải thích:

Chọn ngẫu nhiên 3 học sinh trong số 30 học sinh tham dự đại hội thì có $C_{30}^3=4060$ cách chọn. Do đó n(Ω) = 4060.

Gọi biến cố C: “Trong 3 học sinh được chọn không có học sinh trung bình”.

Tức là ta chỉ chọn ngẫu nhiên 3 học sinh là học sinh khá, giỏi.

Có tất cả 8 + 15 = 23 (học sinh khá, giỏi).

Vì vậy ta có n(C) = $C_{23}^3=1771$.

Vậy xác suất của biến cố C là: $P\left(C\right)=\frac{n\left(C\right)}{n\left(\Omega \right)}=\frac{1771}{4060}=\frac{253}{580}$.

Ta chọn phương án D.

Đáp án: B

Giải thích:

Lớp học có tất cả 20 + 15 = 35 học sinh.

Giáo viên chọn ngẫu nhiên 4 học sinh trong số 35 học sinh của lớp và không tính đến thứ tự thì có $C_{35}^4=52360$ cách chọn.

Tức là n(Ω) = 52 360.

Gọi biến cố H: “Trong 4 học sinh được chọn có cả nam và nữ”.

Khi đó biến cố đối của biến cố H là: $\overline{H}$: “4 học sinh được chọn chỉ có nam hoặc chỉ có nữ”.

Số cách chọn ngẫu nhiên 4 học sinh nam và không tính đến thứ tự là: $C_{20}^4=4845$.

Số cách chọn ngẫu nhiên 4 học sinh nữ và không tính đến thứ tự là: $C_{15}^4=1365$.

Vì vậy n($\overline{H}$) = 4 845 + 1 365 = 6 210.

Khi đó xác suất của biến cố $\overline{H}$ là: $P\left(\overline{H}\right)=\frac{n\left(\overline{H}\right)}{n\left(\Omega \right)}=\frac{6210}{52360}=\frac{621}{5236}$.

Ta có $P\left(H\right)+P\left(\overline{H}\right)=1$.

Suy ra $P\left(H\right)=1-P\left(\overline{H}\right)=1-\frac{621}{5236}=\frac{4615}{5236}$.

Vậy ta chọn phương án B.

Đáp án: A

Giải thích:

+) Gọi số tự nhiên gồm 4 chữ số khác nhau là $\overline{abcd}$.

Có tất có 10 chữ số là {0; 1; 2; …; 9}.

• Chọn a có 9 cách chọn từ các chữ số trong {1; 2; …; 8; 9}.

• Chọn 3 chữ số còn lại trong 9 chữ số và xếp vào 3 vị trí b, c, d có $A_9^3$ cách.

Do đó chọn ngẫu nhiên một số tự nhiên có 4 chữ số khác nhau (có quan tâm đến thứ tự) thì có $9.A_9^3$ = 4 536 cách chọn.

Tức là ta có số phần tử của không gian mẫu n(Ω) = 4 536.

+) Số tự nhiên được chọn gồm 4 số 3; 4; 5; 6.

• Chọn a có 4 cách chọn từ các chữ số trong {3; 4; 5; 6}.

• Chọn b có 3 cách chọn một chữ số từ ba chữ số còn lại sau khi chọn a.

• Chọn c có 2 cách chọn một chữ số từ ba chữ số còn lại sau khi chọn a, b.

• Chọn d có 1 cách chọn một chữ số còn lại sau khi chọn a, b, c.

Số phần tử của A là: n(A) = 4.3.2 = 24.

Hoặc ta cũng có thể tính n(A) như sau:

Chọn 4 chữ số trong tập hợp các chữ số {3; 4; 5; 6} và xếp vào 4 vị trí a, b, c, d sẽ có 4! = 24 cách.

Xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{24}{4536}=\frac{1}{189}$.

Vậy ta chọn phương án A.

Đáp án: A

Giải thích: 

Một tổ có 9 học sinh được xếp thành hàng dọc.

Suy ra số phần tử của không gian mẫu là: n(Ω) = 9!.

Gọi biến cố A: “5 học sinh nam đứng kề nhau”.

• Xếp 5 học sinh nam đứng kề nhau thì sẽ có 5! cách xếp.

• Sau đó ta coi 5 học sinh nam là 1 “người A”, rồi xếp “người A” cùng với 4 bạn nữ kia, tức là xếp 5 người, ta lại có 5! cách xếp.

Vì vậy n(A) = 5!.5!.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{5!.5!}{9!}=\frac{5}{126}$.

Ta chọn phương án A.

Đáp án: D

Giải thích:

⦁ Ta tìm số phần tử của không gian mẫu:

Giai đoạn 1: Chọn 1 tấm thẻ trong số 5 tấm thẻ ở hộp thứ nhất, ta có $C_5^1$ cách chọn.

Giai đoạn 2: Chọn 1 tấm thẻ trong số 5 tấm thẻ ở hộp thứ hai, ta có $C_5^1$ cách chọn.

Giai đoạn 3: Chọn 1 tấm thẻ trong số 5 tấm thẻ ở hộp thứ ba, ta có $C_5^1$ cách chọn.

Theo quy tắc nhân, ta có tất cả $C_5^1.C_5^1.C_5^1=125$ cách chọn.

Do đó n(Ω) = 125.

⦁ Tính số phần tử của biến cố theo yêu cầu bài toán:

Gọi A: “Kết quả thu được là số chẵn”.

Trường hợp 1: 2 thẻ là số lẻ (trong {1; 3; 5}) và 1 thẻ là số chẵn (trong {2; 4}).

Khi đó ta có $C_3^1.C_3^1.C_2^1=18$ cách chọn.

Trường hợp 2: Cả 3 thẻ đều là số chẵn.

Khi đó ta có $C_2^1.C_2^1.C_2^1=8$ cách chọn.

Kết hợp cả hai trường hợp, ta được n(A) = 18 + 8 = 26.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{26}{125}$.

Ta chọn phương án D.

Đáp án: D

Giải thích: 

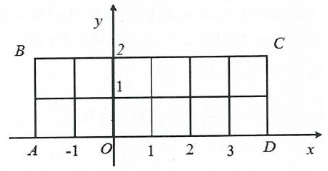
Ta có Ω = {(x; y) | x, y ∈ ℤ; –2 ≤ x ≤ 4 và 0 ≤ y ≤ 2}.

Khi đó x ∈ {–2; –1; 0; 1; 2; 3; 4} và y ∈ {0; 1; 2}.

Chọn 1 hoành độ có 7 cách chọn và chọn 1 tung độ có 3 cách chọn.

Áp dụng quy tắc nhân, ta suy ra n(Ω) = 7.3 = 21 (mỗi điểm là một giao điểm trên hình).

Ta có A: “x, y đều chia hết cho 2”.

Suy ra A = {(x; y) | x ∈ {–2; 0; 2; 4} và y ∈ {0; 2}}.

Chọn 1 hoành độ (chia hết cho 2) có 4 cách chọn và chọn 1 tung độ (chia hết cho 2) thì có 2 cách chọn.

Theo quy tắc nhân, ta có n(A) = 4.2 = 8.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{8}{21}$.

Ta chọn phương án D.

Đáp án: B

Giải thích:

Không gian mẫu của phép thử trên là số cách xếp 4 hành khách lên 4 toa tàu.

Vì chọn mỗi hành khách có 4 cách chọn toa nên ta có 44 cách xếp.

Suy ra số phần tử của không gian mẫu là n(Ω) = 44.

Gọi biến cố A: “1 toa có 3 người, 1 toa có 1 người và 2 toa còn lại không có ai”.

Để tìm số phần tử của biến cố A, ta chia thành hai giai đoạn như sau:

Giai đoạn 1: Chọn 3 hành khách trong số 4 hành khách và chọn 1 toa trong số 4 toa.

Sau đó xếp lên toa đó 3 hành khách vừa chọn.

Khi đó ta có $C_4^3.C_4^1$ cách.

Giai đoạn 2: Chọn 1 toa trong số 3 toa còn lại và xếp 1 hành khách còn lại lên toa đó.

Suy ra có $C_3^1$ cách. Hiển nhiên khi đó 2 toa còn lại sẽ không có hành khách nào.

Theo quy tắc nhân, ta có n(A) = $C_4^3.C_4^1.C_3^1$.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{C_4^3.C_4^1.C_3^1}{4^4}=\frac{3}{16}$.

Ta chọn phương án B.

Đáp án: A

Giải thích:

Chọn ngẫu nhiên 3 câu hỏi trong số 30 câu hỏi trong đề cương để làm đề thi (không tính đến thứ tự) thì có $C_{30}^3=4060$ cách chọn.

Do đó số phần tử của không gian mẫu là: n(Ω) = 4 060.

Gọi biến cố M: “Có ít nhất 2 câu hỏi của đề thi cuối năm nằm trong số 20 câu hỏi đã ôn”.

Ta thấy sẽ xảy ra một trong hai trường hợp sau:

Trường hợp 1: Trong đề thi có đúng 2 câu hỏi trong số 20 câu học sinh đã ôn.

Chọn ngẫu nhiên 2 câu hỏi trong số 20 câu đã ôn (không tính đến thứ tự) thì có $C_{20}^3$ cách chọn.

Chọn ngẫu nhiên 1 câu hỏi còn lại trong 10 câu chưa ôn thì có $C_{20}^2$ cách chọn.

Suy ra trường hợp 1 có $C_{20}^2.C_{10}^1$ cách chọn.

Trường hợp 2: Trong đề thi có cả 3 câu hỏi trong số 20 học sinh đã ôn.

Chọn ngẫu nhiên 3 câu hỏi trong số 20 câu đã ôn (không tính đến thứ tự) thì có $C_{20}^3$ cách chọn.

Kết hợp cả hai trường hợp trên, ta có $n\left(A\right)=C_{20}^2.C_{10}^1+C_{20}^3=3040$.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{3040}{4060}=\frac{152}{203}$.

Ta chọn phương án A.

Đáp án: A

Giải thích: 

Số phần tử của không gian mẫu là: n(Ω) = 6.

Gọi K: “Phương trình x2 + bx + 2 = 0 có hai nghiệm phân biệt”.

Ta có ∆ = b2 – 8.

Phương trình x2 + bx + 2 = 0 có hai nghiệm phân biệt khi và chỉ khi ∆ > 0

⇔ b2 – 8 > 0

$\iff \left[\begin{array}{l}b<-2\sqrt{2}\\ b>2\sqrt{2}\end{array}\right.$

Lại có xúc xắc xuất hiện mặt b chấm nên b ∈ {1; 2; 3; 4; 5; 6}.

Do đó ta nhận b ∈ {3; 4; 5; 6}.

Suy ra n(K) = 4.

Vậy xác suất của biến cố K là: $P\left(K\right)=\frac{n\left(K\right)}{n\left(\Omega \right)}=\frac{4}{6}=\frac{2}{3}$.

Ta chọn phương án A.