50 câu Trắc nghiệm Giải tam giác và ứng dụng thực tế (có đáp án 2024) – Toán 10 Chân trời sáng tạo
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 3: Giải tam giác và ứng dụng thực tế đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 3.
Trắc nghiệm Toán 10 Bài 3: Giải tam giác và ứng dụng thực tế
I. Thông hiểu
Câu 1. Cho ∆ABC có AB = 4, AC = 5 và cosA=35. Độ dài đường cao kẻ từ A bằng:
A. 16√1717;
B. 16√2929;
C. 8;
D. 10.
Hướng dẫn giải
Đáp án: A
Giải thích:
Theo định lí côsin, ta có
BC2 = AB2 + AC2 – 2.AB.AC.cosA
=42+52−2.4.5.35=17.
Suy ra BC=√17.
Nửa chu vi ∆ABC là:
p=AB+AC+BC2=4+5+√172=9+√172.
Diện tích ∆ABC là:
S=√p(p−AB)(p−AC)(p−BC)
=√9+√172(9+√172−4)(9+√172−5)(9+√172−√17)
= 8 (đơn vị diện tích).
Ta
Vậy ta chọn đáp án A.
Câu 2. Cho ∆ABC biết b = 32, c = 45, . Khẳng định nào sau đây đúng?
A. a ≈ 53,8, ;
B. a ≈ 2898,3, ;
C. a ≈ 53,8, ;
D. a ≈ 55,2, ;.
Hướng dẫn giải
Đáp án: A
Giải thích:
Áp dụng định lí côsin cho DABC, ta có:
a2 = b2 + c2 – 2bc.cosA
= 322 + 452 – 2.32.45.cos87°
≈ 2898,3
Suy ra a ≈ ≈ 53,8.
Theo định lí sin, ta có
Suy ra .
Do đó
( không thỏa mãn do
∆ABC có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Vậy a ≈ 53,8, .
Do đó ta chọn phương án A.
Câu 3. Cho ∆ABC. Khẳng định nào sau đây đúng?
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án: A
Giải thích:
Theo hệ quả định lí côsin, ta có .
Diện tích ∆ABC là: .
Ta có
Vậy ta chọn phương án A.
Câu 4. Cho ∆ABC nội tiếp đường tròn bán kính bằng 3, biết . Độ dài bán kính đường tròn nội tiếp ∆ABC gần giá trị nào nhất?
A. 0,88;
B. 0,94;
C. 1,25;
D. 2,15.
Hướng dẫn giải
Đáp án: B
Giải thích:
Bán kính đường tròn ngoại tiếp ∆ABC là R = 3.
∆ABC có (định lí tổng ba góc trong một tam giác)
Suy ra .
Theo hệ quả định lí sin, ta có:
⦁ a = 2R.sinA = 2.3.sin30° = 3.
⦁ b = 2R.sinB = 2.3.sin45° = .
⦁ c = 2R.sinC = 2.3.sin105° = .
Nửa chu vi của ∆ABC là:
.
Ta có S = pr = ab.sinC
⇔ r ≈ 0,94.
Vậy ta chọn phương án B.
Câu 5. Cho ∆ABC biết , c = 14. Khẳng định nào sau đây sai?
A. ;
B. a ≈ 12,3;
C. b ≈ 9,1;
D. Cả A và C đều sai.
Hướng dẫn giải
Đáp án: D
Giải thích:
⦁ ∆ABC có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Do đó phương án A đúng.
⦁ Theo định lí sin, ta có: .
Suy ra .
Do đó phương án B đúng.
Ta có
Suy ra
Do đó phương án C đúng, phương án D sai.
Vậy ta chọn phương án D.
Câu 6. Cho ∆ABC có . Góc lớn nhất của ∆ABC bằng:
A. 80°;
B. 90°;
C. 120°;
D. 150°.
Hướng dẫn giải
Đáp án: C
Giải thích:
Vì nên c < b < a.
Do đó .
Tức là, lớn nhất.
Theo hệ quả định lí côsin, ta có:
.
Suy ra .
Vậy ta chọn phương án C.
Câu 7. Cho ∆ABC thỏa mãn sinC = 2sinB.cosA. Khi đó ∆ABC là:
A. Tam giác tù;
B. Tam giác đều;
C. Tam giác vuông cân;
D. Tam giác cân.
Hướng dẫn giải
Đáp án: D
Giải thích:
• Theo hệ quả định lí sin, ta có:
và .
• Theo hệ quả của định lí côsin, ta có:
.
• Ta có sinC = 2sinB.cosA
⇔ c2 = b2 + c2 – a2
⇔ b2 = a2
⇔ b = a (vì a, b > 0)
Hay AC = BC.
Suy ra ∆ABC cân tại C.
Vậy ta chọn phương án D.
Câu 8. Cho ∆ABC, biết , , R = 6. Khẳng định nào sau đây đúng?
A. ;
B.
C.
D.
Hướng dẫn giải
Đáp án: B
Giải thích:
⦁ Theo hệ quả định lí sin, ta có:
a = 2R.sinA = 2.6.sin60° = .
⦁ Ta có S = .
Suy ra hc = b.sinA
Do đó .
⦁ Theo định lí côsin, ta có a2 = b2 + c2 – 2bc.cosA
Suy ra
Khi đó c2 – 4c – 92 = 0
Vì vậy hoặc .
Vì c là độ dài một cạnh của ∆ABC nên c > 0.
Do đó ta nhận .
Vậy ta chọn phương án B.
Câu 9. Cho ∆ABC biết , b = 2, . Khẳng định nào sau đây đúng nhất?
A. ;
B. ;
C. ;
D. Cả A, B, C đều đúng.
Hướng dẫn giải
Đáp án: D
Giải thích:
Theo hệ quả của định lí côsin, ta có:
⦁ .
Suy ra .
⦁ .
Suy ra .
⦁ .
Suy ra .
Vậy ta chọn phương án D.
Câu 10. Cho , R = 2. Khẳng định nào sau đây sai?
A. ;
B. ;
C. ;
D.
Hướng dẫn giải
Đáp án: C
Giải thích:
Theo hệ quả định lí sin, ta có:
⦁ BC = 2R.sinA = 2.2.sin120° = .
⦁ AC = 2R.sinB = 2.2.sin45° = .
Theo định lí côsin, ta có BC2 = AC2 + AB2 – 2.AC.AB.cosA
Suy ra
Khi đó
Vì vậy hoặc
Vì AB là độ dài một cạnh của ∆ABC nên ta có AB > 0.
Do đó ta nhận .
∆ABC có (định lí tổng ba góc trong một tam giác)
Suy ra .
Vậy ta chọn phương án C.
III. Vận dụng
Câu 1. Cho ∆ABC thỏa mãn sin2A = sinB.sinC. Khẳng định nào sau đây đúng nhất?
A. a2 = bc;
B. ;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Hướng dẫn giải
Đáp án: C
Giải thích:
• Theo hệ quả định lí sin ta có:
, và .
Ta có sin2A = sinB.sinC.
⇔ a2 = bc.
Do đó phương án A đúng.
• Theo hệ quả của định lí côsin, ta có:
.
Áp dụng bất đẳng thức Cauchy cho hai số b, c > 0, ta được b2 + c2 ≥ 2bc.
Do đó ta có .
Vì vậy .
Do đó phương án B đúng.
Vậy ta chọn phương án C.
Câu 2. Cho ∆ABC có a.sinA + b.sinB + c.sinC = ha + hb + hc. Khi đó ∆ABC là:
A. Tam giác cân;
B. Tam giác đều;
C. Tam giác thường;
D. Tam giác vuông.
Hướng dẫn giải
Đáp án: B
Giải thích:
Diện tích ∆ABC là: .
Suy ra .
Diện tích ∆ABC là:
.
Suy ra .
Ta có a.sinA + b.sinB + c.sinC = ha + hb + hc
⇔ a2 + b2 + c2 = bc + ac + ab
⇔ 2a2 + 2b2 + 2c2 = 2bc + 2ac + 2ab
⇔ (a2 – 2ab + b2) + (a2 – 2ac + c2) + (b2 – 2bc + c2) = 0
⇔ (a – b)2 + (a – c)2 + (b – c)2 = 0
⇔ a = b = c.
Vậy ∆ABC là tam giác đều.
Do đó ta chọn phương án B.
Câu 3. Cho ∆ABC biết . Khi đó ∆ABC là:
A. Tam giác cân;
B. Tam giác thường;
C. Tam giác đều;
D. Tam giác vuông.
Hướng dẫn giải
Đáp án: A
Giải thích:
Ta có .
(Áp dụng kết quả Bài tập 5a và 5d, trang 65, Sách giáo khoa, Toán 10, Tập một).
⇔ (sin2A + sin2B)2 = 4.sin2A.sin2B
⇔ sin4A + 2.sin2A.sin2B + sin4B – 4.sin2A.sin2B = 0
⇔ sin4A – 2.sin2A.sin2B + sin4B = 0
⇔ (sin2A – sin2B)2 = 0
⇔ sin2A = sin2B
Theo hệ quả định lí sin, ta được
⇔ a2 = b2
⇔ a = b hay BC = AC.
Vậy ∆ABC cân tại C.
Do đó ta chọn phương án A.
Câu 4. Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C.
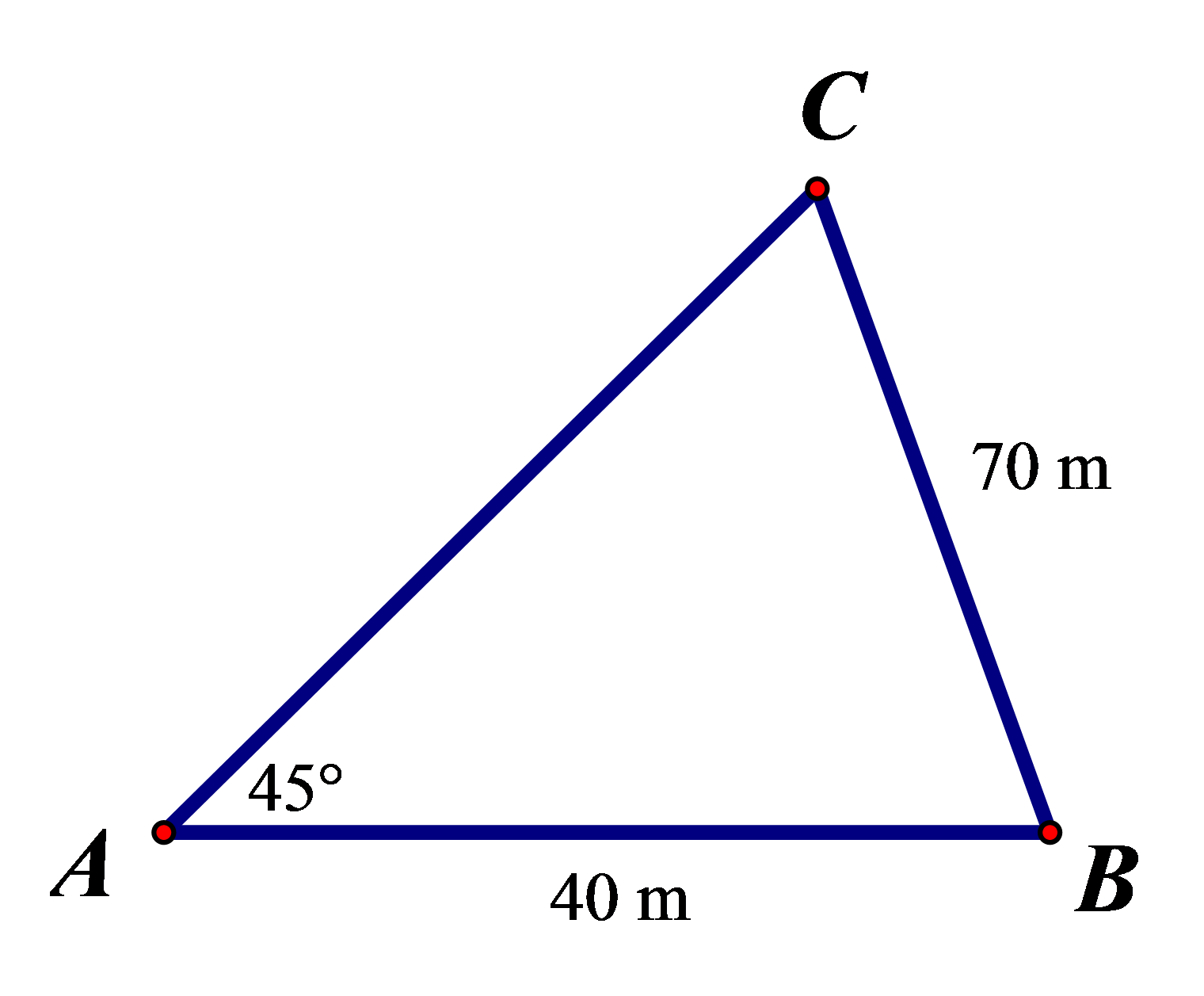
Người ta đo được khoảng cách AB = 40 m, BC = 70 m, . Vậy sau khi đo đạc và tính toán, ta được khoảng cách AC gần nhất với giá trị nào sau đây?
A. 35,7 m;
B. 30,6 m;
C. 92,3 m;
D. 41,5 m.
Hướng dẫn giải
Đáp án: C
Giải thích:
Áp dụng định lí côsin cho ∆ABC, ta được:
BC2 = AB2 + AC2 – 2.AB.AC.cosA
Suy ra 702 = 402 + AC2 – 2.40.AC.cos45°
Do đó
Vì vậy hoặc .
Vì AC > 0 nên ta nhận ≈ 92,3 (m)
Do đó ta chọn phương án C.
Câu 5. Cho ∆ABC thỏa mãn . Khi đó ∆ABC là:
A. Tam giác vuông;
B. Tam giác cân;
C. Tam giác tù;
D. Tam giác đều.
Hướng dẫn giải
Đáp án: A
Giải thích:
• Theo hệ quả của định lí côsin, ta có:
và .
• Theo hệ quả định lí sin, ta có:
.
• Ta có
⇔ sinA(cosB + cosC) = sinB + sinC
⇔ a2b + bc2 – b3 + a2c + b2c – c3 = 2b2c + 2bc2
⇔ b3 + c3 – (a2b + a2c) + (b2c + bc2) = 0
⇔ (b + c)(b2 – bc + c2) – a2(b + c) + bc(b + c) = 0
⇔ (b + c)(b2 – bc + c2 – a2 + bc) = 0
⇔ (b + c)(b2 + c2 – a2) = 0
⇔ b + c = 0 (vô lí vì b, c > 0) hoặc b2 + c2 = a2
⇔ AC2 + AB2 = BC2
Áp dụng định lí Pytago đảo, ta được ∆ABC vuông tại A.
Vậy ta chọn phương án A.