50 câu Trắc nghiệm Hàm số và đồ thị (có đáp án 2024) – Toán 10 Chân trời sáng tạo
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 1: Hàm số và đồ thị đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 1.
Trắc nghiệm Toán 10 Bài 1: Hàm số và đồ thị
I. Nhận biết
Câu 1. Biểu đồ sau đây cho biết tình hình xuất siêu (xuất khẩu trừ nhập khẩu) của nước ta giai đoạn 2017 – Sơ bộ 2021 (Theo số liệu của Tổng cục Thống kê):
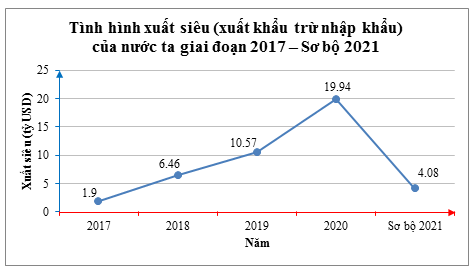
Biểu đồ trên có biểu thị cho ta một hàm số không? Nếu có hãy xác định tập giá trị của hàm số đó.
A. Biểu đồ trên biểu thị một hàm số. Tập giá trị T = {1,9; 6,46; 10,57; 19,94; 4,08};
B. Biểu đồ trên biểu thị một hàm số. Tập giá trị T = {2017; 2018; 2019; 2020; Sơ bộ 2021};
C. Biểu đồ trên biểu thị một hàm số. Tập giá trị T = {1,9; 6,46; 10,57; 19,94; 4,08; 2017; 2018; 2019; 2020; Sơ bộ 2021};
D. Biểu đồ trên không biểu thị một hàm số.
Đáp án: A
Giải thích:
Từ biểu đồ đã cho, ta thấy ứng với mỗi thời điểm (năm) trong biểu đồ đều có một giá trị xuất siêu duy nhất.
Vì vậy biểu đồ trên biểu thị một hàm số.
Hàm số đó có giá trị T = {1,9; 6,46; 10,57; 19,94; 4,08}.
Vậy ta chọn phương án A.
Câu 2. Khi hàm số nghịch biến trên khoảng (a; b) thì đồ thị của hàm số đó có dạng:
A. Đi lên từ trái sang phải;
B. Đi xuống từ trái sang phải;
C. Đi lên rồi đi xuống từ trái sang phải;
D. Đi xuống rồi đi lên từ trái sang phải.
Đáp án: B
Giải thích:
Khi hàm số nghịch biến (giảm) trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.
Do đó ta chọn phương án B.
Câu 3. Cho hàm số y = f(x) xác định trên K. Chọn khẳng định đúng?
A. Hàm số y = f(x) được gọi là nghịch biến trên K nếu ∀x1, x2 ∈ K, x1 < x2 ⇒ f(x1) < f(x2);
B. Hàm số y = f(x) được gọi là đồng biến trên K nếu ∀x1, x2 ∈ K, x1 < x2 ⇒ f(x1) ≤ f(x2);
C. Hàm số y = f(x) được gọi là đồng biến trên K nếu ∀x1, x2 ∈ K, x1 < x ⇒ f(x1) > f(x2);
D. Hàm số y = f(x) được gọi là đồng biến trên K nếu ∀x1, x2 ∈ K, x1 < x2 ⇒ f(x1) < f(x2).
Đáp án: D
Giải thích:
Hàm số y = f(x) đồng biến trên K nếu ∀x1, x2 ∈ K, x1 < x2 ⇒ f(x1) < f(x2).
Hàm số y = f(x) nghịch biến trên K nếu ∀x1, x2 ∈ K, x1 < x2 ⇒ f(x1) > f(x2).
Vậy ta chọn phương án D.
Câu 4. Cho bảng dữ liệu sau về số sản phẩm bán được trong 7 ngày của một cửa hàng thời trang:
|
Ngày |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Số sản phẩm |
25 |
35 |
40 |
30 |
37 |
50 |
60 |
Bảng dữ liệu trên có biểu thị cho ta một hàm số không? Nếu có hãy xác định tập xác định của hàm số đó.
A. Bảng dữ liệu trên không cho ta một hàm số;
B. Bảng dữ liệu trên biểu thị cho ta một hàm số. Tập xác định D = {25; 35; 40; 30; 37; 50; 60};
C. Bảng dữ liệu trên biểu thị cho ta một hàm số. Tập xác định D = {1; 25; 2; 35; 3; 40; 4; 30; 5; 37; 6; 50; 7; 60};
D. Bảng dữ liệu trên biểu thị cho ta một hàm số. Tập xác định D = {1; 2; 3; 4; 5; 6; 7}.
Đáp án: D
Giải thích:
Từ bảng dữ liệu đã cho, ta thấy ứng với mỗi thời điểm (ngày) trong bảng đều có một giá trị số lượng sản phẩm bán được duy nhất.
Vì vậy bảng trên biểu thị một hàm số.
Hàm số đó có tập xác định D = {1; 2; 3; 4; 5; 6; 7}.
Vậy ta chọn phương án D.
Câu 5. Cho bảng dữ liệu sau thống kê về doanh thu mỗi tháng (đơn vị: triệu đồng) của một cửa hàng trong 6 tháng cuối năm 2021:
|
Tháng |
7 |
8 |
9 |
10 |
11 |
12 |
|
Doanh thu |
30 |
35 |
28 |
40 |
50 |
70 |
Tập xác định D và tập giá trị T của hàm số cho bằng bảng trên là:
A. D = {30; 35; 28; 40; 50; 70} và T = {7; 8; 9; 10; 11; 12};
B. D = {7; 8; 9; 10; 11; 12} và T = {30; 35; 28; 40; 50; 70};
C. D = {7; 8; 9; 10; 11; 12; 30; 35; 28; 40; 50; 70} và T = {7; 8; 9; 10; 11; 12};
D. D = {7; 9; 11} và T = {30; 28; 50}.
Đáp án: B
Giải thích:
Ta thấy ứng với mỗi thời điểm (tháng) trong bảng, ta đều có một giá trị doanh thu duy nhất.
Vì vậy biến số x là tháng và y là doanh thu.
Do đó ta có:
+) D = {7; 8; 9; 10; 11; 12};
+) T = {30; 35; 28; 40; 50; 70}.
Vậy ta chọn phương án B.
Câu 6. Đồ thị của hàm số là hình nào trong các hình dưới đây?
A.
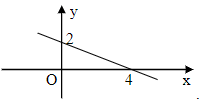
B.
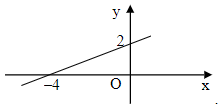
C.
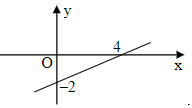
D.
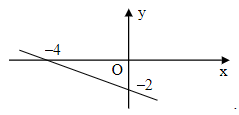
Đáp án: A
Giải thích:
Ta đặt y=f(x)=−x2+2
• Với x = 0, ta có f(0) = −02+2=2
Khi đó đồ thị hàm số đã cho đi qua điểm M(0; 2).
Do đó ta loại phương án C và D.
• Với y = 0, ta có f(x) = −x2+2=0
−x2=−2⇒x=4
Khi đó đồ thị hàm số đã cho đi qua điểm N(4; 0).
Do đó ta loại phương án B.
Vì vậy đồ thị ở phương án A là đồ thị của hàm số đã cho.
Vậy ta chọn phương án A.
Câu 7. Cho biểu đồ sau đây thể hiện tốc độ tăng của nhóm hàng điện tử, máy tính và linh kiện (đơn vị: %) của Việt Nam trong giai đoạn 2015 – 2020 (Theo số liệu của Tổng cục Thống kê):
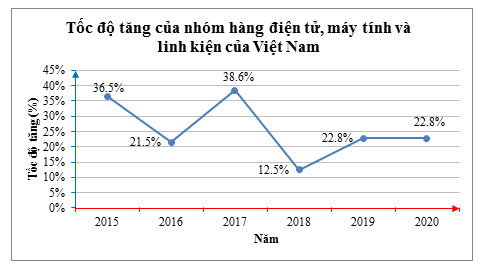
Tập giá trị của hàm số cho bằng biểu đồ trên là:
A. T = {36,5%; 21,5%; 38,6%; 12,5%; 22,8%};
B. T = {2015; 2016; 2017; 2018; 2019; 2020};
C. T = {36,5%; 21,5%; 38,6%; 12,5%; 22,8%; 22,8%};
D. T = {2015; 2016; 2017; 2018; 2019; 2020; 36,5%; 21,5%; 38,6%; 12,5%; 22,8%; 22,8%}.
Đáp án: C
Giải thích:
Ta thấy ứng với mỗi thời điểm (năm) trong biểu đồ, ta đều có một giá trị tốc độ tăng duy nhất.
Vì vậy biến số x là năm và y là tốc độ tăng.
Do đó ta có tập giá trị T = {36,5%; 21,5%; 38,6%; 12,5%; 22,8%; 22,8%}.
Phương án A sai vì không có giá trị 22,8%.
Vậy ta chọn phương án C.
II. Thông hiểu
Câu 1. Xét sự đồng biến, nghịch biến của hàm số f(x)=3x trên khoảng (0; +∞). Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (0; +∞);
B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng (0; +∞);
C. Hàm số đồng biến trên khoảng (0; +∞);
D. Hàm số không đồng biến, không nghịch biến trên khoảng (0; +∞).
Đáp án: A
Giải thích:
Xét hàm số trên khoảng (0; +∞).
Lấy x1, x2 tùy ý thuộc khoảng (0; +∞) sao cho x1 < x2, ta có:
f(x1) – f(x2) = 3x1−3x2=3x2−3x1x1x2=3(x2−x1)x1x2
Vì x1 < x2 nên x2 – x1 > 0 và vì x1, x2 ∈ (0; +∞) nên x1x2 > 0.
Từ đây ta suy ra 3(x2−x1)x1x2>0
Do đó f(x1) – f(x2) > 0 hay f(x1) > f(x2).
Vì vậy hàm số đã cho nghịch biến trên khoảng (0; +∞).
Vậy ta chọn phương án A.
Câu 2. Cho hàm số f(x)={−1x−1, khi x≤0√x+2, khi x>0. Tập xác định của hàm số là tập hợp nào sau đây?
A. [–2; +∞);
B. ℝ;
C. ℝ \ {1};D. {x ∈ ℝ | x ≠ 1 và x ≠ –2}.
Đáp án: B
Giải thích:
Trường hợp 1: x ≤ 0.
Biểu thức f(x) = −1x−1 xác định khi và chỉ khi x – 1 ≠ 0.
Nghĩa là, x ≠ 1.
Giao với điều kiện x ≤ 0, ta được x ≤ 0.
Trường hợp 2: x > 0.
Biểu thức f(x) = √x+2xác định khi và chỉ khi x + 2 ≥ 0.
Nghĩa là, x ≥ –2.
Giao với điều kiện x > 0, ta được x > 0.
Vì vậy khi hợp điều kiện của trường hợp 1 và trường hợp 2, ta thu được tập xác định của hàm số là D = ℝ.
Vậy ta chọn phương án B.
Câu 3. Hàm số y = f(x) có đồ thị như hình vẽ bên.
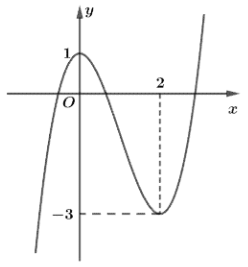
Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (0; 3);
B. Hàm số đồng biến trên khoảng (–∞; 1);
C. Hàm số nghịch biến trên khoảng (0; 2);
D. Hàm số đồng biến trên khoảng (–3; +∞).
Đáp án: C
Giải thích:
Từ đồ thị, ta thấy hàm số xác định trên ℝ.
+) Trên khoảng (–∞; 0), đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (–∞; 0).
+) Trên khoảng (0; 2), đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (0; 2).
+) Trên khoảng (2; +∞), đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (2; +∞).
Phương án A sai vì hàm số đồng biến trên (–∞; 0) và (2; 3); nhưng nghịch biến trên khoảng (0; 2).
Phương án B sai vì hàm số đồng biến trên (–∞; 0) nhưng nghịch biến trên khoảng (0; 1).
Phương án C đúng.
Phương án D sai vì hàm số đồng biến trên (–3; 0) và (2; +∞) nhưng nghịch biến trên khoảng (0; 2).
Vậy ta chọn phương án C.
Câu 4. Xét tính đồng biến, nghịch biến của hàm số y=3√x+3
A. Hàm số đã cho đồng biến trên tập xác định;
B. Hàm số đã cho nghịch biến trên tập xác định;
C. Hàm số đã cho vừa đồng biến, vừa nghịch biến trên tập xác định;
D. Không thể xác định được hàm số đồng biến hay nghịch biến trên tập xác định.
Đáp án: A
Giải thích:
Xét hàm số y=f(x)=3√x+3
Tập xác định của hàm số này là D = ℝ.
Lấy x1, x2 tùy ý thuộc ℝ sao cho x1 < x2, ta có: x1 < x2.
Suy ra 3√x1<3√x2
Khi đó ta có 3√x1+3<3√x2+3
Do đó f(x1) < f(x2).
Vì vậy hàm số đã cho đồng biến (tăng) trên ℝ.
Vậy ta chọn phương án A.
Câu 5. Tập giá trị T của hàm số y=√x+3
A. T = [–3; +∞);
B. T = ℝ;
C. T = [0; +∞);
D. T = ∅.
Đáp án: C
Giải thích:
Ta có √x+3≥0, ∀x∈D
Nghĩa là, y ≥ 0, ∀x ∈ D.
Vì vậy tập giá trị T của hàm số là T = [0; +∞).
Vậy ta chọn phương án C.
Câu 6. Cho hai đại lượng x và y phụ thuộc vào nhau theo các hệ thức dưới đây. Trường hợp nào thì y không phải là hàm số của x?
A. 2x + y = 3;
B. y = x2 – 5;
C. y2 = x + 8;
D. y = 3x3 – 3x + 5.
Đáp án: C
Giải thích:
Ta thấy trong cả bốn hệ thức trên, đại lượng x đều nhận giá trị thuộc tập số D = ℝ.
• Ở ba phương án A, B, D, ta thấy với mỗi giá trị x ∈ ℝ, ta đều xác định được một và chỉ một giá trị tương ứng y ∈ ℝ.
Do đó các hệ thức ở đáp án A, B, D đều cho ta một hàm số.
• Ở phương án C, ta thấy hệ thức đã cho không thỏa mãn định nghĩa hàm số. Cụ thể:
Với x = 1, ta có y2 = 1 + 8 = 9.
Nghĩa là, y = 3 hoặc y = –3.
Do đó tồn tại một giá trị x = 1 ∈ ℝ, ta xác định được hai giá trị tương ứng y ∈ ℝ là y = 3 hoặc y = –3.
Vì vậy hệ thức ở phương án C không cho ta một hàm số y của x.
Vậy ta chọn phương án C.
Câu 7. Điểm nào sau đây thuộc đồ thị hàm số ?
A. M(0; 1);
B. N(2;−34)
C. P(43;0)
D. Q(−2;−14)
Đáp án: D
Giải thích:
Ta đặt f(x)=2x−1x(3x−4)
Biểu thức f(x) có nghĩa khi và chỉ khi x(3x – 4) ≠ 0.
Tức là khi x ≠ 0 và 3x – 4 ≠ 0.
Do đó x ≠ 0 và x≠43
Vì vậy hàm số có tập xác định là D=ℝ\{0;43}
Các điểm M, P có hoành độ lần lượt là 0 và 43 đều không thuộc tập xác định D của hàm số đã cho.
Do đó ta loại phương án A, C.
⦁ Ta xét điểm N(2;−34), ta có hoành độ 2 ∈ D.
Ta có f(2)=2.2−12(3.2−4)=34≠−34
Do đó điểm N(2;−34) không thuộc đồ thị hàm số y=2x−1x(3x−4)
Vì vậy ta loại phương án B.
⦁ Ta xét điểm Q(−2;−14), ta có –2 ∈ D.
Ta có f(−2)=2.(−2)−1−2[3.(−2)−4]=−14
Do đó điểm Q(−2;−14) thuộc đồ thị hàm số y=2x−1x(3x−4)
Vậy ta chọn phương án D.
Câu 8. Tập xác định D của hàm số .
A. D = ℝ \ {0};
B. D = ℝ \ {–1; 0};
C. D = [–1; +∞) \ {0};D. D = [–1; +∞).
Đáp án: C
Giải thích:
Biểu thức f(x) có nghĩa khi và chỉ khi {x+1≥0x≠0
Tức là khi {x≥−1x≠0
Vì vậy tập xác định của hàm số này là D = [–1; +∞) \ {0}.
Vậy ta chọn phương án C.
III. Vận dụng
Câu 1. Tập xác định của hàm số y=f(x)=x2−√2−x(x2−x)√x+1 là:
A. D = (–1; 2] \ {0; 1};
B. D = (–1; 2];
C. D = (–1; 2] \ {0};
D. D = (–1; 2] \ {1}.
Đáp án: A
Giải thích:
Biểu thức f(x) có nghĩa khi và chỉ khi {2−x≥0x2−x≠0x+1>0
Tức là, {x≤2{x≠0x≠1x>−1
Vì vậy {−1<x≤2{x≠0x≠1
Do đó tập xác định của hàm số đã cho là D = (–1; 2] \ {0; 1}.
Vậy ta chọn phương án A.
Câu 2. Gia đình bạn Hoa thuê nhà với giá 5 triệu đồng/tháng và gia đình bạn Hoa phải trả tiền dịch vụ là 1 triệu đồng (tiền dịch vụ chỉ trả một lần khi kết thúc hợp đồng thuê nhà). Gọi x (tháng) là khoảng thời gian gia đình bạn Hoa làm hợp đồng thuê nhà, y (đồng) là số tiền gia đình bạn Hoa cần chi ra trong x tháng. Em hãy viết công thức liên hệ giữa y và x.
A. y = x + 1;
B. y = x + 5;
C. y = 5x + 1;
D. y = 5x + 5.
Đáp án: C
Giải thích:
Vì thuê nhà một tháng hết 5 (triệu đồng).
Nên khi thuê nhà x tháng, số tiền gia đình bạn Hoa phải chi trả là 5x (triệu đồng).
Do phải tốn tiền dịch vụ 1 triệu đồng.
Nên số tiền gia đình bạn Hoa phải trả khi thuê nhà x tháng là 5x + 1 (triệu đồng).
Tức là, y = 5x + 1.
Vậy ta chọn phương án C.
Câu 3. Tìm m để hàm số y=√x−2m+3x−m+3x−1√−x+m+5 xác định trên khoảng (0; 1).
A. m∈[1;32]
B. m ∈ [–3; 0];
C. m ∈ [–3; 0] ∪ [0; 1];
D. m∈[−4;0]∪[1;32]
Đáp án: A
Giải thích:
Ta đặt f(x)=√x−2m+3x−m+3x−1√−x+m+5
Gọi D là tập xác định của hàm số đã cho.
Biểu thức f(x) có nghĩa (x ∈ D) khi và chỉ khi {x−2m+3≥0x−m≠0−x+m+5>0
Tức là, {x≥2m−3x≠mx<m+5
Hàm số đã cho xác định trên khoảng (0; 1) khi và chỉ khi (0; 1) ⊂ D.
Tức là, {2m−3≤0m+5≥1m∉(0;1)
Khi đó ta có {m≤32m≥−4[m≥1m≤0
Vì vậy m∈[−4;0]∪[1;32]
Vậy ta chọn phương án D.
Câu 4. Có bao nhiêu giá trị nguyên của tham số m ∈ [–3; 3] để hàm số f(x) = (m + 1)x + m – 2 đồng biến trên ℝ?
A. 7;
B. 5;
C. 4;
D. 3.
Đáp án: C
Giải thích:
Hàm số đã cho có tập xác định D = ℝ.
Vì hàm số đồng biến trên ℝ nên ta có ∀x1, x2 ∈ D, x1 < x2, suy ra f(x1) < f(x2).
Tức là, (m + 1)x1 + m – 2 < (m + 1)x2 + m – 2.
Do đó (m + 1)(x1 – x2) < 0 (1)
Vì x1 < x2 nên x1 – x2 < 0.
Khi đó (1) tương đương với: m + 1 > 0 hay m > –1.
Mà m ∈ [–3; 3] và m nhận giá trị nguyên.
Nên ta có m ∈ {0; 1; 2; 3}.
Vậy có 4 giá trị nguyên m thỏa yêu cầu bài toán.
Do đó ta chọn phương án C.
Câu 5. Biết rằng hàm số y = f(x) = x3 + 2x + 1 đồng biến trên ℝ. Đặt A=(x2+3x2+1)3+2(x2+3x2+1) và B=8(x2+1)3+4x2+1. Khẳng định nào sau đây đúng?
A. A > B;
B. A = B;
C. A < B;
D. A ≤ B.
Đáp án: A
Giải thích:
Ta có B=8(x2+1)3+4x2+1=(2x2+1)3+2.2x2+1
Ta đặt x1=2x2+1 và x2=x2+3x2+1
Ta có x2=x2+3x2+1=x2+1+2x2+1=x2+1x2+1+2x2+1=1+2x2+1>2x2+1
Ta suy ra x2 > x1 hay x1 < x2.
Vì hàm số đã cho đồng biến trên ℝ và x1 < x2 nên ta có f(x1) < f(x2).
Suy ra (2x2+1)3+2.2x2+1+1<(x2+3x2+1)3+2.x2+3x2+1+1
Do đó (2x2+1)3+2.2x2+1<(x2+3x2+1)3+2.x2+3x2+1
Vì vậy B < A hay A > B.
Vậy ta chọn phương án A.