50 câu Trắc nghiệm Tích vô hướng của hai vectơ (có đáp án 2024) – Toán 10 Chân trời sáng tạo

Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 4: Tích vô hướng của hai vectơ đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 4.

1 90 lượt xem

Bài trước

Bài sau

Trắc nghiệm Toán 10 Bài 4: Tích vô hướng của hai vectơ

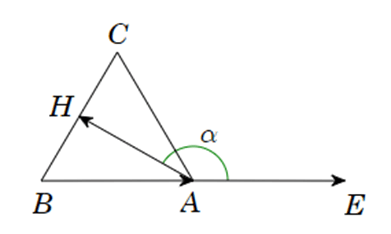
Câu 1. Cho tam giác đều ABC có đường cao AH. Tính $(\vec{A H}, \vec{B A})$ .

A. 30°;

B. 60°;

C. 120°;

D. 150°.

Hướng dẫn giải

Đáp án đúng là: D

15 Bài tập Tích vô hướng của hai vectơ (có đáp án) | Chân trời sáng tạo Trắc nghiệm Toán 10

Vẽ $\vec{A E} = \vec{B A}$ .

Khi đó ta có $(\vec{A H}, \vec{B A}) = (\vec{A H}, \vec{A E}) = \hat{H A E} = α$ .

Tam giác ABC đều có AH là đường cao.

Suy ra AH cũng là đường phân giác của tam giác ABC.

Tam giác ABC đều, suy ra $\hat{B A C} = 60 °$ .

Do đó $\hat{H A B} = \frac{1}{2} \hat{B A C} = \frac{1}{2} .60 ° = 30 °$ .

Ta có: $\hat{H A E} + \hat{H A B} = 180 °$ (hai góc kề bù)

$\Leftrightarrow \hat{H A E} = 180 ° - 30 ° = 150 °$ .

Vậy ta chọn đáp án D.

Câu 2. Cho M, N, P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?

A. $\vec{M N} (\vec{N P} + \vec{P Q}) = \vec{M N} . \vec{N P} + \vec{M N} . \vec{P Q}$ ;

B. $\vec{M P} . \vec{M N} = - \vec{M N} . \vec{M P}$ ;

C. $\vec{M N} . \vec{P Q} = \vec{P Q} . \vec{M N}$ ;

D. $(\vec{M N} - \vec{P Q}) (\vec{M N} + \vec{P Q}) = M N^{2} - P Q^{2}$ .

Hướng dẫn giải

Đáp án đúng là: B

Đáp án A đúng theo tính chất phân phối của tích vô hướng.

Đáp án B sai. Sửa lại: $\vec{M P} . \vec{M N} = \vec{M N} . \vec{M P}$ .

Đáp án C đúng theo tính chất giao hoán của tích vô hướng.

Đáp án D đúng, ta sử dụng bình phương vô hướng và hằng đẳng thức.

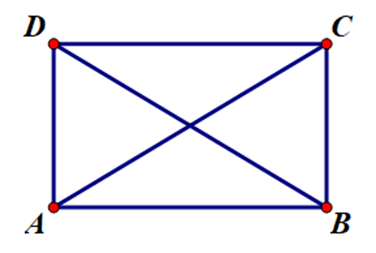
Câu 3. Cho hình chữ nhật ABCD có AB = $\sqrt{2}$ , AD = 1. Tính góc giữa hai vectơ $\vec{A C}$ và $\vec{B D}$ .

A. 89°;

B. 92°;

C. 109°;

D. 91°.

Hướng dẫn giải

Đáp án đúng là: C

15 Bài tập Tích vô hướng của hai vectơ (có đáp án) | Chân trời sáng tạo Trắc nghiệm Toán 10

Tam giác ACD vuông tại D: $\cos \hat{C A D} = \frac{A D}{A C}$ .

Tam giác ABC vuông tại B: $\cos \hat{C A B} = \frac{A B}{A C}$ .

Ta có $\vec{A C} . \vec{B D} = \vec{A C} . (\vec{A D} - \vec{A B}) = \vec{A C} . \vec{A D} - \vec{A C} . \vec{A B}$ .

$= A C . A D . \cos \hat{C A D} - A C . A B . \cos \hat{C A B}$

$= A C . A D . \frac{A D}{A C} - A C . A B . \frac{A B}{A C}$

= AD2 – AB2 = 1 – 2 = –1.

Vì ABCD là hình chữ nhật nên ta có CD = AB = $\sqrt{2}$ và AC = BD.

Tam giác ACD vuông tại D: AC2 = AD2 + CD2 (Định lý Pytago)

$\Leftrightarrow A C^{2} = 1^{2} + {(\sqrt{2})}^{2} = 3$

$\Rightarrow A C = \sqrt{3}$ .

Do đó BD = AC = $\sqrt{3}$ .

Lại có: $\vec{A C} . \vec{B D} = A C . B D . \cos (\vec{A C}, \vec{B D})$

$\Leftrightarrow - 1 = \sqrt{3} . \sqrt{3} . \cos (\vec{A C}, \vec{B D})$

$\Leftrightarrow \cos (\vec{A C}, \vec{B D}) = \frac{- 1}{3}$ .

$\Rightarrow (\vec{A C}, \vec{B D}) \approx 109 ° 28^{'}$ .

Vậy ta chọn đáp án C.

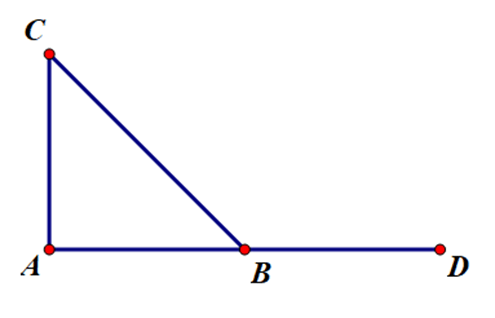
Câu 4. Cho AB = 2cm, BC = 3cm, CA = 5cm. Tính $\vec{C A} . \vec{C B}$ .

A. $\vec{C A} . \vec{C B}$ = 13;

B. $\vec{C A} . \vec{C B}$ = 15;

C. $\vec{C A} . \vec{C B}$ = 17;

D. $\vec{C A} . \vec{C B}$ = 19.

Hướng dẫn giải

Đáp án đúng là: B

Ta có 2 + 3 = 5 (cm). Ta suy ra AB + BC = AC.

Do đó ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C.

(A, B, C không thể là ba đỉnh của tam giác vì không thỏa mãn bất đẳng thức tam giác).

Suy ra $\hat{A C B} = 0 °$ . Do đó $(\vec{C A}, \vec{C B}) = \hat{A C B} = 0 °$ .

Khi đó $\vec{C A} . \vec{C B} = C A . C B . \cos (\vec{C A}, \vec{C B}) = 3.5. \cos 0 ° = 15$ .

Vậy ta chọn đáp án B.

Câu 5. Cho hình vuông ABCD cạnh a. Tính $P = \vec{A C} . (\vec{C D} + \vec{C A})$ .

A. P = – 1;

B. P = 3a2;

C. P = – 3a2;

D. P = 2a2.

Hướng dẫn giải

Đáp án đúng là: C

Tam giác ABC vuông tại B: AC2 = AB2 + BC2 (Định lý Pytago)

⇔ AC2 = a2 + a2 = 2a2

$\Rightarrow A C = a \sqrt{2}$ .

Vì ABCD là hình vuông có AC là đường chéo nên $\hat{A C D} = 45 °$ .

Ta có $P = \vec{A C} . (\vec{C D} + \vec{C A}) = - \vec{C A} . (\vec{C D} + \vec{C A}) = - \vec{C A} . \vec{C D} - {\vec{C A}}^{2}$

$= - C A . C D . \cos (\vec{C A}, \vec{C D}) - C A^{2} = - a \sqrt{2} . a . \cos 45 ° - 2 a^{2} = - 3 a^{2}$ .

Vậy ta chọn đáp án C.

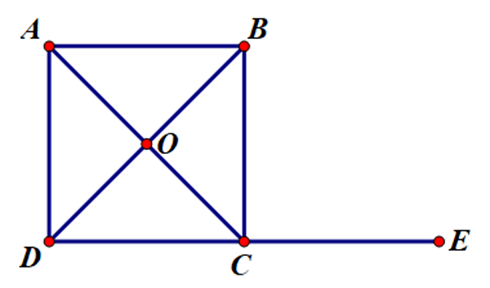
Câu 6. Cho hình vuông ABCD tâm O. Tính tổng $(\vec{A B}, \vec{D C}) + (\vec{A D}, \vec{C B}) + (\vec{C O}, \vec{D C})$ .

A. 45°;

B. 405°;

C. 315°;

D. 225°.

Hướng dẫn giải

Đáp án đúng là: C

15 Bài tập Tích vô hướng của hai vectơ (có đáp án) | Chân trời sáng tạo Trắc nghiệm Toán 10

Ta có $\vec{A B}, \vec{D C}$ cùng hướng nên $(\vec{A B}, \vec{D C}) = 0 °$ .

Ta có $\vec{A D}, \vec{C B}$ ngược hướng nên $(\vec{A D}, \vec{C B}) = 180 °$ .

Vẽ $\vec{C E} = \vec{D C}$ . Khi đó ta có $(\vec{C O}, \vec{D C}) = (\vec{C O}, \vec{C E}) = \hat{O C E}$ .

Vì ABCD là hình vuông có OC là đường chéo nên $\hat{O C B} = 45 °$ .

Ta có BC ⊥ CD (ABCD là hình vuông)

Suy ra BC ⊥ CE, do đó $\hat{B C E} = 90 °$ .

Ta có $\hat{O C E} = \hat{O C B} + \hat{B C E} = 45 ° + 90 ° = 135 °$ .

Vậy $(\vec{A B}, \vec{D C}) + (\vec{A D}, \vec{C B}) + (\vec{C O}, \vec{D C}) = 0 ° + 180 ° + 135 ° = 315 °$ .

Vậy ta chọn đáp án C.

Câu 7. Cho $\vec{a}$ và $\vec{b}$ là hai vectơ cùng hướng và đều khác $\vec{0}$ . Mệnh đề nào sau đây là đúng?

A. $\vec{a} . \vec{b} = (\vec{a}) . (\vec{b})$ ;

B. $\vec{a} . \vec{b} = 0$ ;

C. $\vec{a} . \vec{b} = - 1$ ;

D. $\vec{a} . \vec{b} = - (\vec{a}) . (\vec{b})$ .

Hướng dẫn giải

Đáp án đúng là: A

Ta có $\vec{a} . \vec{b} = (\vec{a}) . (\vec{b}) . \cos (\vec{a}, \vec{b})$ .

Vì $\vec{a}$ và $\vec{b}$ là hai vectơ cùng hướng và đều khác $\vec{0}$ nên $(\vec{a}, \vec{b}) = 0 °$ , suy ra $\cos (\vec{a}, \vec{b}) = 1$ .

Ta suy ra $\vec{a} . \vec{b} = (\vec{a}) . (\vec{b})$

Vậy ta chọn đáp án A.

Câu 8. Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng $(\vec{O A} + \vec{O B}) . \vec{A B} = 0$ là:

A. Tam giác OAB đều;

B. Tam giác OAB cân tại O;

C. Tam giác OAB vuông tại O;

D. Tam giác OAB vuông cân tại O.

Hướng dẫn giải

Đáp án đúng là: B

Ta có $(\vec{O A} + \vec{O B}) . \vec{A B} = 0 \Leftrightarrow (\vec{O A} + \vec{O B}) . (\vec{O B} - \vec{O A}) = 0$

$\Leftrightarrow {\vec{O B}}^{2} - {\vec{O A}}^{2} = 0$

⇔ OB2 – OA2 = 0

⇔ OB = OA.

Do đó tam giác OAB cân tại O.

Vậy ta chọn đáp án B.

Câu 9. Cho tam giác đều ABC có cạnh a. Tính tích vô hướng $\vec{A B} . \vec{A C}$ .

A. $\vec{A B} . \vec{A C} = 2 a^{2}$ ;

B. $\vec{A B} . \vec{A C} = - \frac{a^{2} \sqrt{3}}{2}$ ;

C. $\vec{A B} . \vec{A C} = - \frac{a^{2}}{2}$ ;

D. $\vec{A B} . \vec{A C} = \frac{a^{2}}{2}$ .

Hướng dẫn giải

Đáp án đúng là: D

Ta có $(\vec{A B}, \vec{A C}) = \hat{B A C} = \hat{A}$ .

Tam giác ABC đều nên $\hat{A} = 60 °$ .

Do đó $(\vec{A B}, \vec{A C}) = \hat{A} = 60 °$ .

Suy ra $\vec{A B} . \vec{A C} = A B . A C . \cos (\vec{A B}, \vec{A C}) = a . a . \cos 60 ° = \frac{a^{2}}{2}$ .

Vậy ta chọn đáp án D.

Câu 10. Cho hai vectơ $\vec{a}$ và $\vec{b}$ thỏa mãn $(\vec{a}) = 3$ , $(\vec{b}) = 2$ và $\vec{a} . \vec{b} = - 3$ . Xác định góc α giữa hai vectơ $\vec{a}$ và $\vec{b}$ .

A. α = 30°;

B. α = 45°;

C. α = 60°;

D. α = 120°.

Hướng dẫn giải

Đáp án đúng là: D

Ta có $\vec{a} . \vec{b} = (\vec{a}) . (\vec{b}) . \cos (\vec{a}, \vec{b})$

$\Leftrightarrow \cos (\vec{a}, \vec{b}) = \frac{\vec{a} . \vec{b}}{(\vec{a}) . (\vec{b})} = \frac{- 3}{3.2} = \frac{- 1}{2}$

$\Rightarrow (\vec{a}, \vec{b}) = 120 °$ .

Vậy ta chọn đáp án D.

Câu 11.Cho tam giác ABC có BC = a, CA = b, AB = c. Tính $P = (\vec{A B} + \vec{A C}) . \vec{B C}$ .

A. P = b2 – c2;

B. $P = \frac{b^{2} + c^{2}}{2}$ ;

C. $P = \frac{c^{2} + b^{2} + a^{2}}{3}$ ;

D. $P = \frac{c^{2} + b^{2} - a^{2}}{2}$ .

Hướng dẫn giải

Đáp án đúng là: A

Ta có $P = (\vec{A B} + \vec{A C}) . \vec{B C} = (\vec{A B} + \vec{A C}) (\vec{B A} + \vec{A C})$

$= (\vec{A C} + \vec{A B}) (\vec{A C} - \vec{A B}) = {\vec{A C}}^{2} - {\vec{A B}}^{2} = A C^{2} - A B^{2} = b^{2} - c^{2}$ .

Vậy ta chọn đáp án A.

Câu 12. Cho hình chữ nhật ABCD có AB = 8, AD = 5. Tính $\vec{A B} . \vec{B D}$ .

A. $\vec{A B} . \vec{B D}$ = 62;

B. $\vec{A B} . \vec{B D}$ = 64;

C. $\vec{A B} . \vec{B D}$ = –62;

D. $\vec{A B} . \vec{B D}$ = –64.

Hướng dẫn giải

Đáp án đúng là: D

Vì giả thiết không cho góc nên ta sẽ phân tích các vectơ $\vec{A B}, \vec{B D}$ theo các vectơ vuông góc với nhau.

Vì ABCD là hình chữ nhật nên AB ⊥ BC.

Suy ra $\vec{A B} ⊥ \vec{B C}$ .

Do đó $\vec{A B} . \vec{B C} = 0$ .

Theo quy tắc hình bình hành ta có: $\vec{B D} = \vec{B A} + \vec{B C}$ .

Ta có $\vec{A B} . \vec{B D} = \vec{A B} . (\vec{B A} + \vec{B C}) = \vec{A B} . \vec{B A} + \vec{A B} . \vec{B C}$

$= - \vec{A B} . \vec{A B} + 0 = - {\vec{A B}}^{2} = - A B^{2} = - 64$ .

Vậy ta chọn đáp án D.

Câu 13. Cho tam giác ABC vuông tại A và AB = AC = a. Tính $\vec{A B} . \vec{B C}$ .

A. $\vec{A B} . \vec{B C} = - a^{2}$ ;

B. $\vec{A B} . \vec{B C} = a^{2}$ ;

C. $\vec{A B} . \vec{B C} = - \frac{a^{2} \sqrt{2}}{2}$ >;

D. $\vec{A B} . \vec{B C} = \frac{a^{2} \sqrt{2}}{2}$ .

Hướng dẫn giải

Đáp án đúng là: A

15 Bài tập Tích vô hướng của hai vectơ (có đáp án) | Chân trời sáng tạo Trắc nghiệm Toán 10

Vẽ $\vec{B D} = \vec{A B}$ .

Ta có $(\vec{A B}, \vec{B C}) = (\vec{B D}, \vec{B C}) = \hat{C B D}$ .

Tam giác ABC vuông cân tại A. Ta suy ra $\hat{A B C} = 45 °$ .

Ta có $\hat{A B C} + \hat{C B D} = 180 °$ (hai góc kề bù)

Khi đó ta được $\hat{C B D} = 180 ° - 45 ° = 135 °$ .

Tam giác ABC vuông cân tại A: BC2 = AB2 + AC2 (Định lý Pytago)

⇔ BC2 = 2a2

$\Rightarrow B C = a \sqrt{2}$ .

Do đó $\vec{A B} . \vec{B C} = A B . B C . \cos (\vec{A B}, \vec{B C}) = a . a \sqrt{2} . \cos 135 ° = - a^{2}$ .

Vậy ta chọn đáp án A.

Câu 14. Cho tam giác ABC. Tập hợp các điểm M thỏa mãn $\vec{M A} (\vec{M B} + \vec{M C}) = 0$ là:

A. một điểm;

B. đường thẳng;

C. đoạn thẳng;

D. đường tròn.

Hướng dẫn giải

Đáp án đúng là: D

Gọi I là trung điểm BC. Ta suy ra $\vec{M B} + \vec{M C} = 2 \vec{M I}$ .

Ta có $\vec{M A} (\vec{M B} + \vec{M C}) = 0 \Leftrightarrow \vec{M A} .2 \vec{M I} = 0 \Leftrightarrow \vec{M A} . \vec{M I} = 0 \Leftrightarrow \vec{M A} ⊥ \vec{M I}$ (*)

Biểu thức (*) chứng tỏ MA ⊥ MI hay M nhìn đoạn AI dưới một góc vuông.

Do đó tập hợp các điểm M là một đường tròn đường kính AI.

Vậy ta chọn đáp án D.

Câu 15. Cho tam giác ABC. Tập hợp các điểm M thỏa mãn $\vec{M A} . \vec{B C} = 0$ là:

A. một điểm;

B. đường thẳng;

C. đoạn thẳng;

D. đường tròn.

Hướng dẫn giải

Đáp án đúng là: B

Ta có $\vec{M A} . \vec{B C} = 0 \Leftrightarrow \vec{M A} ⊥ \vec{B C} \Leftrightarrow M A ⊥ B C$ .

Vậy tập hợp các điểm M là đường thẳng đi qua A và vuông góc với BC.

Vậy ta chọn đáp án B.

1 90 lượt xem

Bài trước

Bài sau

50 câu Trắc nghiệm Tích vô hướng của hai vectơ (có đáp án 2024) – Toán 10 Chân trời sáng tạo

Giới thiệu

Liên kết

Chính sách

Kết nối

50 câu Trắc nghiệm Tích vô hướng của hai vectơ (có đáp án 2024) – Toán 10 Chân trời sáng tạo

CHỌN BỘ SÁCH BẠN MUỐN XEM