50 câu Trắc nghiệm Nhị thức Newton (có đáp án 2024) – Toán 10 Chân trời sáng tạo
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 3: Nhị thức Newton đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 3.
Trắc nghiệm Toán 10 Bài 3: Nhị thức Newton
I. Nhận biết
Câu 1. Số hạng tử trong khai triển (a + b)99 bằng
A. 97;
B. 98;
C. 99;
D. 100.
Hướng dẫn giải
Đáp án: D
Giải thích:
Ta có trong khai triển (a + b)n có n + 1 hạng tử
Vậy trong khai triển (a + b)99 có 100 hạng tử
Câu 2. Phát biểu nào sau đây đúng?
A. (a + b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4;
B. (a – b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4;
C. (a + b)4 = a4 + 4a3b – 6a2b2 + 4ab3 + b4;
D. (a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4.
Hướng dẫn giải
Đáp án: D
Giải thích:
Theo công thức nhị thức Newton, ta có:
⦁ (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4.
Do đó phương án A, C sai.
⦁ (a – b)4 = a4 + 4a3(–b) + 6a2(–b)2 + 4a(–b)3 + (–b)4
= a4 – 4a3b + 6a2b2 – 4ab3 + b4.
Do đó phương án B sai, phương án D đúng.
Vậy ta chọn phương án D.
Câu 3. Hệ số tự do trong khai triển (x + 1)n với n ∈ ℤ, n ≥ 1 là:
A. n + 1;
B. n;
C. n – 1;
D. 1.
Hướng dẫn giải
Đáp án: D
Giải thích:
Ta có:
(x + 1)n
=C0n.xn.10+C1n.xn−1.11+C2n.xn−2.12+...+Cn−1n.x1.1n−1+Cnn.x0.1n
=C0n.xn+C1n.xn−1+C2n.xn−2+...+Cn−1n.x1+Cnn
Do đó số hạng không chứa biến trong khai triển trên là Cnn=1.
Vậy hệ số tự do của khai triển là 1.
Câu 4. Tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (m + 2n)5 bằng
A. 4;
B. 5;
C. 6;
D. 7.
Hướng dẫn giải
Đáp án: B
Giải thích:
Ta có tổng số mũ của a, b trong mỗi hạng tử khi khai triển (a + b)n luôn bằng n.
Vậy tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (a + b)5 bằng 5.
Câu 5. Phát biểu nào sau đây đúng?
A. (a + b)5 = a5 + 5a4b – 10a3b2 + 10a2b3 – 5ab4 + b5;
B. (a – b)5 = a5 – 5a4b + 10a3b2 – 10a2b3 + 5ab4 + b5;
C. (a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5;
D. (a – b)5 = a5 + 5a4b – 10a3b2 + 10a2b3 – 5ab4 + b5.
Hướng dẫn giải
Đáp án: C
Giải thích:
Theo công thức nhị thức Newton, ta có:
⦁ (a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5.
Do đó phương án A sai, phương án C đúng.
⦁ (a – b)5 = a5 + 5a4(–b) + 10a3(–b)2 + 10a2(–b)3 + 5a(–b)4 + (–b)5
= a5 – 5a4b + 10a3b2 – 10a2b3 + 5ab4 – b5.
Do đó phương án B, D sai.
Vậy ta chọn phương án C.
Câu 6. Biểu thức C04.x4+C14.x3y+C24.x2y2+C34.xy3+C44.y4 bằng:
A. (x + y)4;
B. (x – y)4;
C. (x + y)5;
D. (x – y)5.
Hướng dẫn giải
Đáp án: A
Giải thích:
Theo công thức nhị thức Newton, ta có:
C04.x4+C14.x3y+C24.x2y2+C34.xy3+C44.y4=(x+y)4.
Vậy ta chọn phương án A.
Câu 7. Khai triển của biểu thức (2+√5)4 là:
A. 24−4.23.√5+6.22.(√5)2−4.2.(√5)3+(√5)4;
B. 24+4.23.√5+6.22.(√5)2+4.2.(√5)3+(√5)4;
C. 24+5.23.√5+10.22.(√5)2+5.2.(√5)3+(√5)4;
D. 24+4.23.√5−6.22.(√5)2+4.2.(√5)3+(√5)4.
Hướng dẫn giải
Đáp án: B
Giải thích:
Theo công thức nhị thức Newton, ta có:
(2+√5)4=24+4.23.√5+6.22.(√5)2+4.2.(√5)3+(√5)4.
Vậy ta chọn phương án B.
II. Thông hiểu
Câu 1. Hệ số của số hạng chứa ab3 trong khai triển (a + 2b)4 là:
A. 32ab3;
B. 32;
C. 8;
D. 8ab3.
Hướng dẫn giải
Đáp án: B
Giải thích:
Cách 1: Ta có:
(a + 2b)4
= a4 + 4a3.2b + 6a2.(2b)2 + 4a.(2b)3 + (2b)4
= a4 + 8a3b + 24a2b2 + 32ab3 + 16b4
Số hạng chứa ab3 trong khai triển (a + 2b)4 là: 32ab3.
Vậy hệ số chứa ab3 trong khai triển (a + 2b)4 là 32.
Do đó ta chọn phương án B.
Cách 2:
Số hạng tổng quát trong khai triển (a + 2b)4 là:
Ck4a4−k(2b)k (với 0 ≤ k ≤ 4 và k ∈ ℤ).
=Ck4a4−k2kbk=2kCk4a4−kbk
Để số hạng trên là số hạng chứa ab3 thì {4−k=1k=3⇔k=3(tm)
Khi đó ta có số hạng đó là 23C34a4−3b3=32a3b
Vậy hệ số của số hạng chứa ab3 trong khai triển (a + 2b)4 là 32.
Câu 2. Cho x là số thực dương, số hạng chứa x trong khai triển (x+2√x)4 là:
A. 24x;
B. 12x;
C. 24;
D. 12.
Hướng dẫn giải
Đáp án: A
Giải thích:

Câu 3. Biết rằng trong khai triển (x2+ax)5 (với x ≠ 0), hệ số của số hạng chứa 1x3 là 640. Khi đó giá trị của a bằng:
A. a = 4;
B. a = –4;
C. n ∈ {–4; 4};
D. a ∈ ∅.
Hướng dẫn giải
Đáp án: C
Giải thích:
Cách 1: Ta có
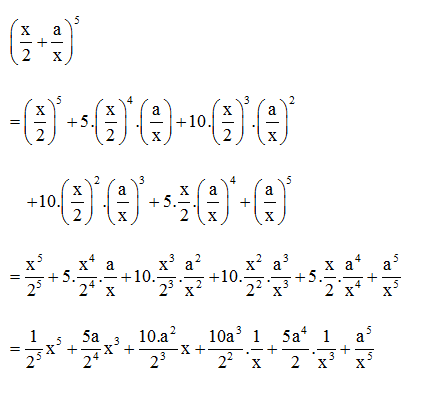

Cách 2:
Số hạng tổng quát trong khai triển (x2+ax)5 là:
Ck5(x2)5−k(ax)k (với 0 ≤ k ≤ 5 và k ∈ ℤ).
=Ck5.x5−k25−k.akxk=Ck5ak25−k.x5−2k
Để số hạng trên là số hạng chứa 1x3 thì 5 – 2k = – 3 hay k = 4.
Khi đó ta có số hạng đó là C45a425−4.x5−2.4=5a42.x−3=5a42.1x3
Do đó hệ số của số hạng chứa ab3 trong khai triển (x2+ax)5là 5a42.
Theo đề, ta có hệ số của số hạng chứa 1x3 là 640.
Tức là, 5a42=640.
Tương tự như cách 1 ta tìm được a = 4 hoặc a = –4.
Vậy ta chọn phương án C.
Câu 4. Cho x là số thực dương. Khai triển nhị thức (x2+1x)4, ta có hệ số của số hạng chứa xm bằng 6. Giá trị của m là:
A. m = 6;
B. m = 8;
C. m = 2;
D. m = 2 hoặc m = 6.
Hướng dẫn giải
Đáp án: C
Giải thích:
Theo công thức nhị thức Newton, ta có:
(x2+1x)4=(x2)4+4.(x2)3.1x+6.(x2)2.(1x)2+4.x2.(1x)3+(1x)4=x8+4.x6.1x+6.x4.1x2+4.x2.1x3+1x4=x8+4.x5+6.x2+4.1x+1x4.
Ta thấy số hạng có hệ số bằng 6 là 6x2.
Suy ra m = 2.
Vậy ta chọn phương án C.
Câu 5. Giá trị n nguyên dương thỏa mãn A2n−Cn−1n+1=5 là:
A. n = –2;
B. n = 5;
C. n ∈ {–2; 5};
D. n ∈ ∅.
Hướng dẫn giải
Đáp án: D
Giải thích:
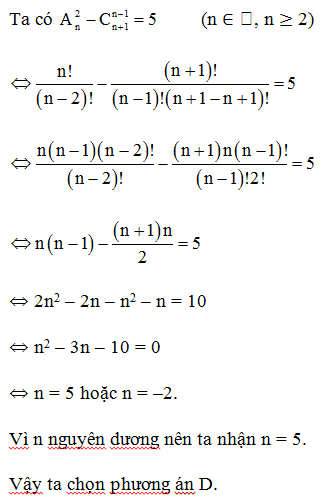
Câu 6. Số hạng chứa x3y trong khai triển (xy+1y)5 là:
A. 3x3y;
B. 5x3y;
C. 10x3y;
D. 4x3y.
Hướng dẫn giải
Đáp án: C
Giải thích:
Cách 1: Ta có:
(xy+1y)5=C05(xy)5(1y)0+C15(xy)4(1y)1+C25(xy)3(1y)2+C35(xy)2(1y)3+C45(xy)1(1y)4+C55(xy)0(1y)5=x5y5+5x4y4.y−1+10x3y3.y−2+10x2y2.y−3+5xy.y−4+y-5=x5y5+5x4y3+10x3y+10x2y−1+5xy−3+y−5
Vậy số hạng chứa x3y trong khai triển (xy+1y)5 là 10x3y.
Cách 2:
Số hạng tổng quát trong khai triển (xy+1y)5 là:
Ck5(xy)5−k(1y)k (với 0 ≤ k ≤ 5 và k ∈ ℤ).
=Ck5x5−ky5−ky−k=Ck5x5−ky5−2k
Để số hạng trên là số hạng chứa x3y thì {5−k=35−2k=1⇔k=2(tm)
Khi đó ta có số hạng đó là C25x5−2y5−2.2=10x3y
Vậy số hạng chứa x3y trong khai triển (xy+1y)5 là 10x3y.
Do đó ta chọn phương án C.
Câu 7. Số hạng không chứa x trong khai triển P(x)=(x3−1x2)5 (x ≠ 0) (theo chiều số mũ của x giảm dần) là số hạng thứ:
A. 3;
B. 6;
C. 4;
D. 5.
Hướng dẫn giải
Đáp án: C
Giải thích:
Theo nhị thức Newton, ta có:
P(x)=(x3−1x2)5=(x3)5+5.(x3)4.(−1x2)+10.(x3)3.(−1x2)2+10.(x3)2.(−1x2)3+5.x3.(−1x2)4+(−1x2)5=x15−5.x12.1x2+10.x9.1x4−10.x6.1x6+5.x3.1x8−1x10=x15−5.x10+10.x5−10+5.1x5−1x10
Ta thấy số hạng không chứa x là số hạng thứ 4 (theo chiều số mũ của x giảm dần).
Vậy ta chọn phương án C.
Câu 8. Giá trị của biểu thức (3+√2)4+(3−√2)4 bằng:
A. 193;
B. –386;
C. 772;
D. 386.
Hướng dẫn giải
Đáp án: D
Giải thích:
Áp dụng công thức nhị thức Newton, ta có:

III. Vận dụng
Câu 1. Số hạng chính giữa trong khai triển (x3 + xy)22 là:
A. C1122.x42.y12;
B. C1322.x41.y11;
C. C1222.x43.y11;
D. C1222.x42.y12.
Hướng dẫn giải
Đáp án: D
Giải thích:
Số hạng tổng quát của khai triển (x3 + xy)22 là:
Ck22(x3)22−k(xy)k (với 0 ≤ k ≤ 22 và k ∈ ℤ)
=Ck22.x66−3k.xk.yk=Ck22.x66−2k.yk
(x3 + xy)22 có số mũ là 22 nên khai triển này có 23 số hạng.
Do đó số hạng chính giữa là số hạng thứ 12 ứng với k = 11.
Vậy số hạng chính giữa của khai triển là C1222.x42.y12.
Câu 2. Hệ số của số hạng x10 trong khai triển (1 + x + x2 + x3)5 là:
A. 5;
B. 50;
C. 101;
D. 105.
Hướng dẫn giải
Đáp án: C
Giải thích:
Ta có (1 + x + x2 + x3)5 = [1 + x + x2(1 + x)]5
= [(1 + x)(1 + x2)]5 = (1 + x)5.(1 + x2)5.
Theo công thức nhị thức Newton, ta có:
⦁ A = (1 + x)5
= 15 + 5.14.x + 10.13.x2 + 10.12.x3 + 5.1.x4 + x5
= 1 + 5x + 10x2 + 10x3 + 5x4 + x5.
⦁ B = (1 + x2)5
= 15 + 5.14.x2 + 10.13.(x2)2 + 10.12.(x2)3 + 5.1.(x2)4 + (x2)5
= 1 + 5x2 + 10x4 + 10x6 + 5x8 + x10.
Suy ra (1 + x + x2 + x3)5 = A.B
Khi đó ta có số hạng chứa x10 trong khai triển (1 + x + x2 + x3)5 là:
xi.xj = x10 hay xi + j = x10 với xi là lũy thừa của số hạng trong A, xj là lũy thừa của số hạng trong B (i ∈ {0; 1; 2; 3; 4; 5} và j ∈ {0; 2; 4; 6; 8; 10}).
Do đó ta có bảng sau:
|
j |
i |
|
10 |
0 |
|
8 |
2 |
|
6 |
4 |
Từ bảng ta có số hạng chứa x10 trong khai triển là:
1.x10 + 10x2.5x8 + 5x4.10x6
= x10 + 50x10 + 50x10 = 101x10.
Vậy hệ số của số hạng chứa x10 trong khai triển (1 + x + x2 + x3)5 là 101.
Do đó ta chọn phương án C.
Câu 3. Cho tập hợp M = {1; 2; 3; 4}. Số tập con của tập M là:
A. 8;
B. 16;
C. 32;
D. 5.
Hướng dẫn giải
Đáp án: B
Giải thích:
Ta thấy tập hợp M có 4 phần tử.
• Mỗi tập con của M có k phần tử (với 1 ≤ k ≤ 4) là một tổ hợp chập k của 4 phần tử.
Do đó số tập con như vậy bằng Ck4.
• Mặt khác, có một tập con của M không có phần tử nào (tập rỗng).
Tức là, có C04=1 tập con như vậy.
Do đó số tập con của tập hợp M là:
C04+C14+C24+C34+C44 = 16 (tập con).
Vậy ta chọn phương án B.
Câu 4. Cho biểu thức (2 + x)n, biết n là số nguyên dương thỏa mãn A3n+2A2n=100. Khi đó số hạng của x3 trong khai triển biểu thức (2 + x)n là:
A. –40;
B. –40x3;
C. 40x3;
D. 80x3.
Hướng dẫn giải
Đáp án: C
Giải thích:
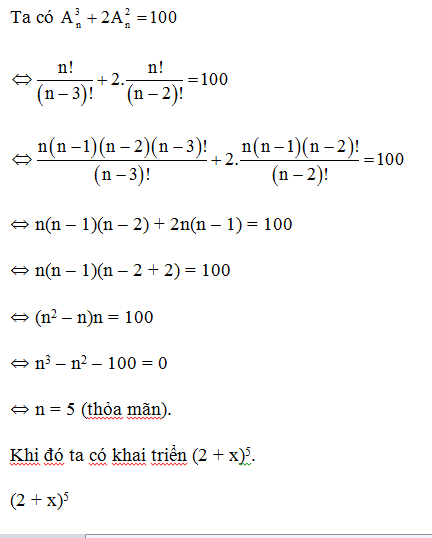
⇔ n(n – 1)(n – 2) + 2n(n – 1) = 100
⇔ n(n – 1)(n – 2 + 2) = 100
⇔ (n2 – n)n = 100
⇔ n3 – n2 – 100 = 0
⇔ n = 5 (thỏa mãn).
Khi đó ta có khai triển (2 + x)5.
(2 + x)5
= 25 + 5.24.x + 10.23.x2 + 10.22.x3 + 5.2.x4 + x5
= 32 + 80x + 80x2 + 40x3 + 10x4 + x5
Vậy số hạng của x3 trong khai triển biểu thức (2 + x)5 là 40x3.
Do đó ta chọn phương án C.
Câu 5. Tổng S=C05+3C15+32C25+33C35+34C45+35C55 bằng:
A. S = 35;
B. S = 25;
C. S = 3.25;
D. S = 45.
Hướng dẫn giải
Đáp án: D
Giải thích:
Theo công thức nhị thức Newton, ta có:
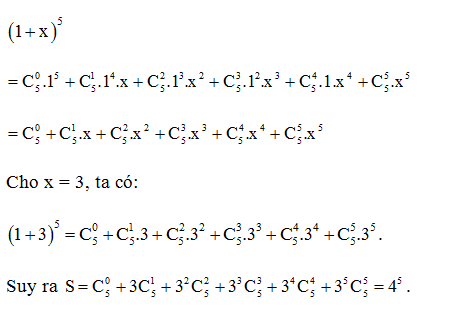
Vậy ta chọn phương án D.