50 câu Trắc nghiệm Giá trị lượng giác của một góc từ 0° đến 180° (có đáp án 2024) – Toán 10 Chân trời sáng tạo

Đáp án: B

Giải thích:

Cách 1: Sử dụng bảng giá trị lượng giác của một số góc đặc biệt

Quan sát bảng giá trị lượng giác của một số góc đặc biệt, ta có $\sin 30°=\frac{1}{2}$

Cách 2: Sử dụng máy tính cầm tay

Để tính sin30°, ta ấn liên tiếp các phím sau đây: $\boxed{\sin }\boxed{3}\boxed{0}\boxed{°\text{'}\text{'}\text{'}}\boxed{)}\boxed{=}$

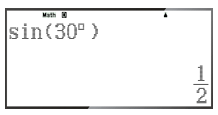
Ta thu được kết quả $\sin 30°=\frac{1}{2}$

Vậy ta chọn phương án B.

Đáp án: A

Giải thích:

Với điểm $M\left(\frac{4}{5};\frac{3}{5}\right)$, ta có $\widehat{xOM}=\alpha$. Khi đó theo định nghĩa, ta có:

⦁ sinα = yM = $\frac{3}{5}$;

⦁ cosα = xM = $\frac{4}{5}$.

Vậy ta chọn phương án A.

Đáp án: C

Giải thích:

Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có:

⦁ sin(90° – α) = cosα;

⦁ tan(90° – α) = cotα.

Do đó ta chọn phương án C.

Đáp án: A

Giải thích:

Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có cos(180° – α) = –cosα.

Do đó ta chọn phương án A.

Đáp án: D

Giải thích:

Nếu góc α thỏa mãn 90° ≤ α ≤ 180° thì α là góc tù.

Khi đó sinα > 0, cosα < 0, tanα < 0, cotα < 0.

Do đó ta chọn phương án D.

Đáp án: C

Giải thích:

Với mỗi góc α  (0° ≤ α ≤ 180°) thì tỉ số $\frac{y_0}{x_0}$ (x0 ≠ 0) là tan của góc α và ta kí hiệu là $\tan \alpha =\frac{y_0}{x_0}$.

Do đó ta chọn phương án C.

Đáp án: B

Giải thích:

Ta có tan103° = tan(180° – 77°) = –tan77°.

Vậy ta chọn phương án B.

Đáp án: C

Giải thích:

Ta có M = sin50° + cos70° + cos110° – sin130°

= sin50° + cos70° + cos(180° – 70°) – sin(180° – 50°)

= sin50° + cos70° – cos70° – sin50°

= (sin50° – sin50°) + (cos70° – cos70°)

= 0 + 0

= 0.

Vậy ta chọn phương án C.

Đáp án: B

Giải thích:

Ta có H = cot5°.cot10°.cot15°…cot80°.cot85°

= cot5°.cot10°.cot15°…cot(90° – 10°).cot(90° – 5°)

= cot5°.cot10°.cot15°…tan10°.tan5°

= (cot5°.tan5°).(cot10°.tan10°)…(cot40°.tan40°).cot45°

= 1.1…1.cot(45°)           (Áp dụng kết quả Bài tập 5b, trang 65, Sách giáo khoa Toán 10, Tập một)

= cot45°

= 1.

Vậy ta chọn phương án B.

Đáp án: A

Giải thích:

Với 0° ≤ α, β ≤ 180° và α + β = 180° ta có:

⦁ sinα = sin(180° – β) = sinβ;

⦁ cosα = cos(180° – β) = –cosβ.

Suy ra P = sinα.cosα + sinβ.cosβ

= sinβ.(–cosβ) + sinβ.cosβ

= 0.

Vậy ta chọn phương án A.

Đáp án: A

Giải thích:

Để tính cot26°32’54’’, ta cần tính tan26°32’54’’ trước.

Ta sử dụng máy tính cầm tay bấm liên tiếp các phím sau:

$\boxed{\tan }\boxed{2}\boxed{6}\boxed{°\text{'}\text{'}\text{'}}\boxed{3}\boxed{2}\boxed{°\text{'}\text{'}\text{'}}\boxed{5}\boxed{4}\boxed{°\text{'}\text{'}\text{'}}\boxed{)}\boxed{=}$

Ta thu được kết quả tan26°32’54’’ ≈ 0,4996353264.

Vì $\tan x=\frac{1}{\cot x}$ hay $\cot x=\frac{1}{\tan x}$.

Nên để tìm cot26°32’54’’, ta bấm liên tiếp các phím: $\boxed{1}\boxed{÷}\boxed{\text{Ans\hspace{0.17em}}}$

Ta thu được kết quả cot26°32’54’’ ≈ 2,001.

Vậy ta chọn phương án A.

Đáp án: D

Giải thích:

Ta có sin80° = sin(90° – 10°) = cos10°.

Và sin80° = sin(180° – 100°) = sin100°.

Vậy ta chọn phương án D.

Đáp án: C

Giải thích:

Cách 1:

Quan sát bảng giá trị lượng giác của một số góc đặc biệt, ta có tanx không xác định khi x = 90°.

Vì vậy x = 90°.

Cách 2:

Theo định nghĩa, ta có $\tan x=\frac{y_0}{x_0}=\frac{\sin x}{\cos x}$.

Khi đó tanx không xác định khi và chỉ khi cosx = 0.

Đến đây ta có thể sử dụng máy tính cầm tay hoặc sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta thu được cosx = 0 khi x = 90°.

Vậy ta chọn phương án C.

Đáp án: C

Giải thích:

Ta có B = 3 – sin290° + 2cos260° – 3tan245°.

= 3 – 12 + 2.${\left(\frac{1}{2}\right)}^2$ – 3.12 = $-\frac{1}{2}$.

Vậy ta chọn phương án C.

Đáp án: D

Giải thích:

Ta có A = a2sin90° + b2cos90° + c2cos180°.

= a2.1 + b2.0 + c2.(–1) = a2 – c2.

Do đó ta chọn phương án D.

Đáp án: C

Giải thích:

Ta có M = sin245° – 2sin250° + 3cos245° – 2sin2130° + 4tan55°.tan35°

$={\left(\frac{\sqrt{2}}{2}\right)}^2-2{\sin }^{2}50°+3.{\left(\frac{\sqrt{2}}{2}\right)}^2-2{\sin }^2\left(180°-50°\right)+4\tan 55°.\tan \left(90°-55°\right)$

= 2 – 2(sin250° + cos250°) + 4tan55°.cot55°

= 2 – 2.1 + 4.1     (Áp dụng kết quả Bài tập 5a và 5b, trang 65, Sách giáo khoa Toán 10, Tập một)

= 4.

Vậy ta chọn phương án C.

Đáp án: D

Giải thích:

∆ABC có: A + B + C = 180° (định lí tổng ba góc trong một tam giác)

⦁ Ta có $\sin \frac{A+B}{2}=\sin \frac{180°-C}{2}$

$=\sin \left(\frac{180°}{2}-\frac{C}{2}\right)$

$=\sin \left(90°-\frac{C}{2}\right)$

= tan(90° – C)

Do đó phương án A đúng.

⦁ Ta có $\tan \frac{A+B-C}{2}=\tan \frac{180°-C-C}{2}$

$=\tan \frac{180°-2C}{2}$

$=\tan \left(\frac{180°}{2}-\frac{2C}{2}\right)$

= tan(90° – C)

= cotC.

Do đó phương án B đúng.

⦁ Ta có cos(A + B) = cos(180° – C)

= –cosC.

Do đó phương án C đúng.

Vậy ta chọn phương án D.

Đáp án: D

Giải thích:

Vì tanα = –3 nên  do đó cosα ≠ 0.

Ta có $H=\frac{6\sin \alpha -7\cos \alpha }{6\cos \alpha +7\sin \alpha }$

$=\frac{6.\frac{\sin \alpha }{\cos \alpha }-7.\frac{\cos \alpha }{\cos \alpha }}{6.\frac{\cos \alpha }{\cos \alpha }+7.\frac{\sin \alpha }{\cos \alpha }}$        (vì cosα ≠ 0)

$=\frac{6.\tan \alpha -7}{6+7.\tan \alpha }$

$=\frac{6.\left(-3\right)-7}{6+7.\left(-3\right)}=\frac{5}{3}$

Vậy ta chọn phương án D.

Đáp án: B

Giải thích:

Ta có sinα – cosα = $\frac{1}{\sqrt{5}}$.

$\Rightarrow 1-2\sin \alpha \cos \alpha =\frac{1}{5}$ (Vì sin2α + cos2α = 1, áp dụng Bài tập 5a, trang 65, Sách giáo khoa Toán 10, Tập một)

$\Rightarrow 2\sin \alpha \cos \alpha =\frac{4}{5}$

$\Rightarrow \sin \alpha \cos \alpha =\frac{2}{5}$

$\Rightarrow {\sin }^2\alpha {\cos }^2\alpha =\frac{4}{25}$

Ta có $E=\sqrt{{\sin }^4\alpha +{\cos }^4\alpha }$

Đáp án: D

Giải thích:

Ta có $2\cos \alpha +\sqrt{2}\sin \alpha =2$

$\iff \sqrt{2}\sin \alpha =2-2\cos \alpha$

⇒ 2sin2α = (2 – 2cosα)2

⇔ 2(1 – cos2α) = 4 – 8cosα + 4cos2α

⇔ 6cos2α – 8cosα + 2 = 0   (1)

Đặt t = cosα.

Vì 0° < α < 90° nên 0 < t < 1.

Phương trình (1) tương đương với: 6t2 – 8t + 2 = 0

$\iff \left[\begin{array}{l}t=1\\ t=\frac{1}{3}\end{array}\right.$

Vì 0 < t < 1 nên ta nhận $\frac{1}{3}$.

Với $t=\frac{1}{3}$, ta có $\cos \alpha =\frac{1}{3}$.

Suy ra ${\cos }^2\alpha =\frac{1}{9}$

Áp dụng Bài tập 5a, trang 65, Sách giáo khoa Toán 10, Tập một, ta có:

sin2α + cos2α = 1

$\iff {\sin }^2\alpha =1-{\cos }^2\alpha =1-\frac{1}{9}=\frac{8}{9}$

$\iff \left[\begin{array}{l}\sin \alpha =\frac{2\sqrt{2}}{3}\\ \sin \alpha =-\frac{2\sqrt{2}}{3}\end{array}\right.$

Vì 0° < α < 90° nên α là góc nhọn.

Do đó sinα > 0.

Vì vậy ta nhận $\sin \alpha =\frac{2\sqrt{2}}{3}$

Ta có $\cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{1}{3}:\frac{2\sqrt{2}}{3}=\frac{1}{3}.\frac{3}{2\sqrt{2}}=\frac{1}{2\sqrt{2}}=\frac{\sqrt{2}}{4}$.

Vậy ta chọn phương án D.