50 câu Trắc nghiệm Mệnh đề (có đáp án 2024) – Toán 10 Chân trời sáng tạo
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 1: Mệnh đề đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 1.
Trắc nghiệm Toán 10 Bài 1: Mệnh đề
I. Nhận biết
Câu 1. Cho hai mệnh đề P và Q. Điều kiện để mệnh đề P Þ Q sai là:
A. P đúng và Q đúng;
B. P sai và Q đúng;
C. P đúng và Q sai;
D. P sai và Q sai.
Đáp án: C
Giải thích:
Mệnh đề P Þ Q chỉ sai khi P đúng và Q sai.
Vậy ta chọn đáp án C.
Câu 2. Cho hai mệnh đề P và Q. Phát biểu mệnh đề P Û Q nào sau đây sai?
A. P khi và chỉ khi Q;
B. P tương đương Q;
C. P là điều kiện cần để có Q;
D. P là điều kiện cần và đủ để có Q.
Đáp án: C
Giải thích:
Mệnh đề P Û Q được phát biểu bằng một trong ba cách sau:
⦁ P khi và chỉ khi Q. Do đó phương án A đúng.
⦁ P tương đương Q. Do đó phương án B đúng.
⦁ P là điều kiện cần và đủ để có Q (hay Q là điều kiện cần và đủ để có P). Do đó phương án D đúng, phương án C sai.
Vậy ta chọn phương án C.
Câu 3. Chọn phát biểu đúng trong các phát biểu dưới đây.
A. Mệnh đề “∀x ∈ M, P(x)” đúng nếu với mọi x0 ∈ M sao cho P(x0) là mệnh đề đúng;
B. Mệnh đề “∃x ∈ M, P(x)” đúng nếu có x0 ∈ M sao cho P(x0) là mệnh đề sai;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Đáp án: A
Giải thích:
Phát biểu ở phương án A đúng.
Phát biểu ở phương án B sai.
Sửa lại: Mệnh đề “∃x ∈ M, P(x)” đúng nếu có x0 ∈ M sao cho P(x0) là mệnh đề đúng.
Vậy phương án A đúng, phương án B, C, D sai.
Do đó ta chọn phương án A.
Câu 4. Mệnh đề A Þ B được hiểu như thế nào?
A. A khi và chỉ khi B;
B. B suy ra A;
C. A là điều kiện cần để có B;
D. A là điều kiện đủ để có B.
Đáp án: D
Giải thích:
Khi mệnh đề A Þ B là định lí, ta nói A là điều kiện đủ để có B.
Vậy ta chọn phương án D.
Câu 5. Cho các phát biểu sau:
(I) Mệnh đề P và mệnh đề phủ định 
của nó có tính đúng sai trái ngược nhau;
(II) Khi P đúng thì 
sai;
(III) Khi P sai thì 
sai.
Số các phát biểu đúng là:
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án: C
Giải thích:
Phát biểu (I) đúng.
Vì phát biểu (I) đúng nên ta có khi P đúng thì 
sai và khi P sai thì 
đúng.
Do đó phát biểu (II) đúng, phát biểu (III) sai.
Vậy có 2 phát biểu đúng là (I), (II).
Do đó ta chọn phương án C.
Câu 6. Câu nào trong các câu sau không phải là mệnh đề chứa biến?
A. 3n là số lẻ (n là số tự nhiên);
B. x2 + 1 > 0;
C. 2 – x2 < 0;
D. 4 + x.
Đáp án: D
Giải thích:
Các câu ở phương án A, B, C đúng vì là mệnh đề chứa biến.
Câu ở phương án D chỉ là một biểu thức, không phải là mệnh đề chứa biến.
Do đó phương án D sai.
Vậy ta chọn phương án D.
Câu 7. Trong các câu sau, câu nào là mệnh đề?
A. Hôm nay là thứ mấy?
B. Các bạn làm bài đi!
C. Hôm nay trời rất đẹp.
D. Việt Nam là một nước thuộc châu Á.
Đáp án: D
Giải thích:
Phương án A: “Hôm nay là thứ mấy?” là câu hỏi, không khẳng định được tính đúng sai. Do đó đây không phải là một mệnh đề.
Phương án B: “Các bạn làm bài đi!” là câu cảm thán, không khẳng định được tính đúng sai. Do đó đây không phải là một mệnh đề.
Phương án C: “Hôm nay trời rất đẹp.” không khẳng định tính đúng sai do không đưa ra tiêu chí thế nào là trời rất đẹp. Do đó đây không phải là một mệnh đề.
Phương án D: “Việt Nam là một nước thuộc châu Á.” là một mệnh đề (mệnh đề đúng).
Vậy ta chọn phương án D.
II. Thông hiểu
Câu 1. Mệnh đề “Mọi số thực cộng với số đối của nó đều bằng 0” được viết bằng kí hiệu là:
A. ∃x ∈ ℝ: x + (–x) = 0;
B. ∀x ∈ ℝ: x + (–x) = 0;
C. ∃x ∈ ℤ: x – x = 0;
D. ∀x ∈ ℝ: x – x = 0.
Đáp án: B
Giải thích:
Ta có thể viết lại mệnh đề “Mọi số thực cộng với số đối của nó đều bằng 0” như sau:
∀x ∈ ℝ: x + (–x) = 0.
Vậy ta chọn phương án B.
Câu 2. Cho mệnh đề: “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”. Phát biểu mệnh đề trên bằng cách sử dụng thuật ngữ “điều kiện cần” là:
A. Tứ giác là hình thang cân là điều kiện cần để tứ giác đó có hai đường chéo bằng nhau;
B. Tứ giác có hai đường chéo bằng nhau là điều kiện cần để tứ giác đó là hình thang cân;
C. Nếu tứ giác không phải là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau;
D. Cả A, B, C đều sai.
Đáp án: B
Giải thích:
Trong mệnh đề P Þ Q: “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”, ta thấy:
⦁ P: “Một tứ giác là hình thang cân”;
⦁ Q: “Tứ giác có hai đường chéo bằng nhau”.
Do đó ta có phát biểu sau:
“Tứ giác có hai đường chéo bằng nhau là điều kiện cần để tứ giác đó là hình thang cân”.
Vậy ta chọn phương án A.
Câu 3. Cho mệnh đề: “Nếu hai góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?
A. Nếu hai góc bằng nhau thì hai góc đó ở vị trí so le trong;
B. Nếu hai góc không ở vị trí so le trong thì hai góc đó không bằng nhau;
C. Nếu hai góc không bằng nhau thì hai góc đó không ở vị trí so le trong;
D. Nếu hai góc ở vị trí so le trong thì hai góc đó không bằng nhau.
Đáp án: A
Giải thích:
Trong mệnh đề: “Nếu hai góc ở vị trí so le trong thì hai góc đó bằng nhau”, ta thấy:
⦁ P: “Hai góc ở vị trí so le trong”;
⦁ Q: “Hai góc đó bằng nhau”.
Mệnh đề P Þ Q có mệnh đề đảo là mệnh đề Q Þ P.
Mệnh đề Q Þ P được phát biểu như sau: “Nếu hai góc bằng nhau, thì hai góc đó ở vị trí so le trong”.
Vậy ta chọn phương án A.
Câu 4. Cho mệnh đề: “Nếu a + b < 2 thì một trong hai số a và b nhỏ hơn 1”. Phát biểu mệnh đề trên bằng cách sử dụng thuật ngữ “điều kiện đủ” là:
A. a + b < 2 là điều kiện đủ để một trong hai số a và b nhỏ hơn 1;
B. Một trong hai số a và b nhỏ hơn 1 là điều kiện đủ để a + b < 2;
C. Nếu một trong hai số a và b nhỏ hơn 1 thì a + b < 2;
D. Cả A, B, C đều sai.
Đáp án: A
Giải thích:
Trong mệnh đề P Þ Q: “Nếu a + b < 2 thì một trong hai số a và b nhỏ hơn 1”, ta thấy:
⦁ P: “a + b < 2”;
⦁ Q: “Một trong hai số a và b nhỏ hơn 1”.
Do đó ta có phát biểu sau:
“a + b < 2 là điều kiện đủ để một trong hai số a và b nhỏ hơn 1”.
Vậy ta chọn phương án A.
Câu 5. Mệnh đề phủ định của mệnh đề P: “2x – 3 ≤ 0” là:
A. 
: “2x – 3 < 0”;
B. 
: “2x – 3 > 0”;
C. 
: “2x – 3 ≥ 0”;
D. 
: “2x – 3 ≠ 0”.
Đáp án: B
Giải thích:
Mệnh đề phủ định của mệnh đề P là 
: “2x – 3 > 0”.
Vậy ta chọn phương án B.
Câu 6. Cho mệnh đề chứa biến: P(x): “x + 15 ≤ x2” (x là số thực).
Mệnh đề nào sau đây đúng?
A. P(0);
B. P(5);
C. P(3);
D. P(4).
Đáp án: B
Giải thích:
Với x = 0, ta có P(0): “0 + 15 ≤ 02” là mệnh đề sai.
Với x = 5, ta có P(5): “5 + 15 ≤ 52” là mệnh đề đúng.
Với x = 3, ta có P(3): “3 + 15 ≤ 32” là mệnh đề sai.
Với x = 4, ta có P(4): “4 + 15 ≤ 42” là mệnh đề sai.
Vậy ta chọn phương án B.
Câu 7. Cho hai mệnh đề P và Q. Điều kiện để mệnh đề P Û Q đúng là:
A. P đúng và Q sai;
B. 
đúng và Q đúng;
C. P sai và Q đúng;
D. 
sai và 
sai.
Đáp án: D
Giải thích:
Mệnh đề P Û Q đúng khi cả hai mệnh đề P Þ Q và Q Þ P đều đúng.
Mệnh đề P Þ Q đúng khi P đúng và Q đúng.
Mệnh đề Q Þ P đúng khi P đúng và Q đúng.
Vì vậy mệnh đề P Û Q đúng khi cả P và Q đều đúng.
Nghĩa là cần phải thỏa mãn một trong ba trường hợp sau:
⦁ 
sai (vì P đúng) và Q đúng.
⦁ P đúng và 
sai.
⦁ 
sai và 
sai.
Vậy ta chọn phương án D.
Câu 8. Mệnh đề “∃x ∈ ℝ: x2 = 4” khẳng định rằng:
A. Bình phương của mỗi số thực bằng 4;
B. Có ít nhất một số thực mà bình phương của nó bằng 4;
C. Chỉ có một số thực bình phương bằng 4;
D. Nếu x là một số thực thì x2 = 4.
Đáp án: B
Giải thích:
Mệnh đề “∃x ∈ ℝ: x2 = 4” có nghĩa là tồn tại (có ít nhất) một số thực x sao cho bình phương của nó bằng 4.
Do đó phương đáp án B đúng.
Phương án A sai vì kí hiệu trong mệnh đề là “∃” không phải “∀”.
Phương án C sai vì kí hiệu “∃” có nghĩa là “tồn tại” hay “có ít nhất”.
Phương án D sai vì mệnh đề “Nếu P thì Q” là mệnh đề kéo theo.
Vậy ta chọn phương án B.
III. Vận dụng
Câu 1. Mệnh đề nào sau đây là sai?
A. Phương trình x2 + bx + c = 0 có nghiệm Û b2 – 4c ≥ 0;
B.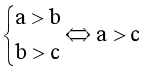 
;
C. ∆ABC vuông tại A Û 
;
D. π < 4 Û π2 < 16.
Đáp án: B
Giải thích:
⦁ Phương trình x2 + bx + c = 0 có nghiệm Û ∆ ≥ 0.
Û b2 – 4c ≥ 0.
Do đó phương án A đúng.
⦁ Nếu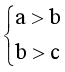 
(hay a > b > c) thì a > c.
Do đó mệnh đề P Þ Q đúng (1)
Ta xét mệnh đề đảo Q Þ P: a > c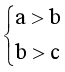 
.
Ta chọn a, b, c sao cho Q đúng.
Chọn a = 4; c = 2; b = 1.
Vì 4 > 2 nên ta suy ra a > c, tức là Q đúng.
Khi đó ta có 4 > 2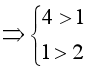 
.
Lúc này P vô lý vì 1 < 2.
Do đó Q đúng và P sai.
Vì vậy mệnh đề đảo Q Þ P sai (2)
Từ (1), (2), ta suy ra phương án B sai.
Đến đây ta có thể chọn phương án B.
⦁ Nếu ∆ABC vuông tại A thì 
.
∆ABC có: 
(định lí tổng ba góc trong một tam giác).
Suy ra 
.
Vì vậy mệnh đề P Þ Q đúng (3)
Nếu thì
:
∆ABC có: 
(định lí tổng ba góc trong một tam giác).
Suy ra 
.
Do đó ∆ABC vuông tại A.
Vì vậy mệnh đề Q Þ P đúng (4)
Từ (1), (2), ta suy ra P Û Q.
Do đó phương án C đúng.
⦁ Ta có π ≈ 3,14 < 4.
Suy ra π2 ≈ 9,87 < 16.
Do đó P Þ Q đúng (5)
Ngược lại, ta có π2 ≈ 9,87 < 16.
Suy ra π ≈ 3,14 < 4.
Do đó Q Þ P đúng (6)
Từ (5), (6), ta suy ra P Û Q.
Do đó phương án D đúng.
Vậy ta chọn phương án B.
Câu 2. Cho mệnh đề A: “
”. Khẳng định nào sau đây là đúng?
A. 
: “
” và A sai, 
đúng;
B. 
: “
” và A đúng, 
đúng;
C. 
: “
” và A đúng, 
sai;
D. 
: “
” và A đúng, 
sai.
Đáp án: C
Giải thích:
Mệnh đề phủ định của mệnh đề A là 
: “
”.
Do đó ta loại phương án B, D.
Vì 
nên mệnh đề A đúng.
Vì vậy mệnh đề 
sai.
Do đó phương án C đúng, phương án A sai.
Vậy ta chọn phương án C.
Câu 3. Cho mệnh đề “∀x ∈ ℝ, x2 – 2 + a > 0, với số a ∈ ℝ”. Số a để mệnh đề trên đúng là:
A. a < 2;
B. a ≤ 2;
C. a = 2;
D. a > 2.
Đáp án: D
Giải thích:
Vì x2 – 2 + a > 0, ∀x ∈ ℝ
Û x2 > 2 – a, ∀x ∈ ℝ (*)
Mà x2 ≥ 0, ∀x ∈ ℝ
Do đó (*) Û 2 – a < 0
Û a > 2.
Vậy ta chọn phương án D.
Câu 4. Kí hiệu A là tập hợp các cầu thủ x trong đội tuyển bóng rổ, P(x) là mệnh đề chứa biến “x cao trên 180 cm”. Mệnh đề “∀x ∈ A, P(x)” khẳng định rằng:
A. Mọi cầu thủ trong đội tuyển bóng rổ đều cao trên 180 cm;
B. Trong số các cầu thủ của đội tuyển bóng rổ có một số cầu thủ cao trên 180 cm;
C. Bất cứ ai cao trên 180 cm đều là cầu thủ của đội tuyển bóng rổ;
D. Có một số người cao trên 180 cm là cầu thủ của đội tuyển bóng rổ.
Đáp án: A
Giải thích:
Mệnh đề “∀x ∈ X, P(x)” khẳng định rằng: “Mọi cầu thủ trong đội tuyển bóng rổ đều cao trên 180 cm”.
Do đó ta chọn phương án A.
Câu 5. Cho mệnh đề A: “∀x ∈ ℝ: x2 + x ≥ ”. Chọn khẳng định đúng:
A. 
: “∃x ∈ ℝ: x2 + x ≥ 
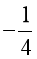” và đây là mệnh đề đúng;
B. 
: “∃x ∈ ℝ: x2 + x ≤ 
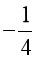” và đây là mệnh đề đúng;
C. 
: “∃x ∈ ℝ: x2 + x < 
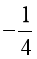” và đây là mệnh đề đúng;
D. 
: “∃x ∈ ℝ: x2 + x < 
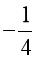” và đây là mệnh đề sai.
Đáp án: D
Giải thích:
Mệnh đề A: “∀x ∈ ℝ: x2 + x ≥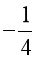 
”.
Mệnh đề phủ định của mệnh đề A là:
: “∃x ∈ ℝ: x2 + x <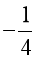 
”.
Ta xét x2 + x <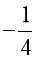 
.
.
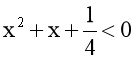Û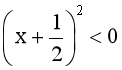 
, điều này vô lý.
Vì vậy mênh đề 
sai.
Vậy ta chọn phương án D.