Lý thuyết Bội chung và bội chung nhỏ nhất (Cánh diều 2024) Toán 6

Lý thuyết Toán lớp 6 Bài 13: Bội chung và bội chung nhỏ nhất

Video giải Toán 6 Bài 13: Bội chung và bội chung nhỏ nhất - Cánh diều

A. Lý thuyết Bội chung và bội chung nhỏ nhất

I. Bội chung và bội chung nhỏ nhất

1. Bội chung: Số tự nhiên n được gọi là bội chung của hai số a và b nếu n vừa là bội của a vừa là bội của b.

Quy ước: Viết tắt bội chung là BC. 

Kí hiệu: Tập hợp các bội chung của a và b là BC(a, b). 

Ví dụ: Các bội của 2 là: 0, 2, 4, 6, 8, 10, 12,…

Các bội của 3 là: 0, 3, 6, 9, 12,…

Các bội chung của 2 và 3 là: 0, 6, 12, … 

Vậy BC(2, 3) = {0; 6; 12; …} . 

Chú ý: Số tự nhiên n được gọi là bội chung của ba số a, b, c nếu n là bội của cả ba số a, b, c. Ta kí hiệu: Tập hợp các bội chung của a, b, c là BC(a, b, c).

Ví dụ: 20 chia hết cho 2 nên 20 là bội của 2, 20 chia hết cho 4 nên 20 là bội của 4, 20 chia hết cho 5 nên 20 là bội của 5. Do đó 20 là một bội chung của ba số 2, 4, 5. 

2. Bội chung nhỏ nhất: Số nhỏ nhất khác 0 trong các bội chung của a và b được gọi là bội chung nhỏ nhất của a và b.

Quy ước: Viết tắt bội chung nhỏ nhất là BCNN.

Kí hiệu: bội chung nhỏ nhất của a và b là BCNN(a, b).

Ví dụ: Ta có các bội chung của 2 và 3 là: 0, 6, 12,… Số nhỏ nhất khác 0 trong các bội chung của 2 và 3 là 6 nên 6 là bội chung nhỏ nhất của 2 và 3. 

Vậy BCNN(2, 3) = 6. 

Chú ý: 

+ Số nhỏ nhất khác 0 trong các bội chung của ba số a, b, c được gọi là bội chung nhỏ nhất của ba số a, b, c.

+ Kí hiệu: bội chung nhỏ nhất của a, b, c là BCNN(a, b, c).

+ Bội chung nhỏ nhất của hai số nguyên tố cùng nhau bằng tích của hai số đó. 

Ví dụ: 5 và 8 là hai số nguyên tố cùng nhau nên BCNN(5, 8) = 5 . 8 = 40. 

3. Tìm bội chung thông qua BCNN

+ Bội chung của nhiều số là bội của bội chung nhỏ nhất của chúng.

+ Để tìm bội chung của nhiều số, ta có thể lấy bội chung nhỏ nhất của chúng lần lượt nhân với 0, 1, 2, …

Ví dụ: Biết BCNN(a, b) = 30. Tìm tất cả các số có hai chữ số là bội chung của a và b.

Lời giải:

Vì bội chung của a và b đều là bội của BCNN(a, b) = 30 nên tất cả các số có hai chữ số là bội chung của a và b là: 30, 60, 90.

II. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố 

Các bước tìm BCNN bằng cách phân tích các số ra thừa số nguyên tố

Bước 1: Phân tích mỗi số ra thừa số nguyên tố

Bước 2: Chọn ra các thừa số nguyên tố chung và các thừa số nguyên tố riêng

Bước 3: Với mỗi thừa số nguyên tố chung và riêng, ta chọn lũy thừa với số mũ lớn nhất

Bước 4: Lấy tích của các lũy thừa đã chọn, ta nhận được bội chung nhỏ nhất cần tìm.

Ví dụ: Tìm BCNN(40, 48).

Lời giải:

Ta có: 40 = 23 . 5; 48 = 24 . 3

Chọn ra các thừa số nguyên tố chung và riêng của 40 và 48, đó là 2, 3, 5.

Số mũ lớn nhất của 2 là 4; Số mũ lớn nhất của 3 là 1; Số mũ lớn nhất của 5 là 1.

Vậy BCNN(40, 48) = 24  . 3 . 5 = 240.

Chú ý: Nếu   thì BCNN(a, b) = a. Chẳng hạn: BCNN(48, 16) = 48.

III. Ứng dụng bội cung nhỏ nhất vào cộng, trừ các phân số không cùng mẫu

Để tính tổng (hoặc hiệu) hai hay nhiều phân số không cùng mẫu, ta có thể làm như sau:

+ Quy đồng mẫu số hai phân số bằng cách chọn mẫu chung là BCNN của các mẫu. 

+ Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

+ Sau khi nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng, ta cộng (trừ) hai hay nhiều phân số có cùng mẫu. 

Ví dụ: Thực hiện phép tính:

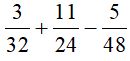
Lời giải:

BCNN(32, 24, 48) = 96

96 : 32 = 3; 96 : 24 = 4; 96 : 48 = 2

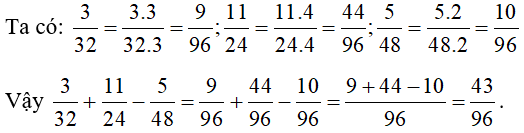
B. Bài tập tự luyện

Bài 1. Thực hiện phép tính sau: .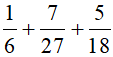

Lời giải:

Để thực hiện phép tính, trước hết tìm bội chung nhỏ nhất của 6, 27 và 18 để quy đồng mẫu số.

+ Ta có: 6 = 2 . 3; 27 = 33; 18 = 2 . 9 = 2 . 32 

Các thừa số nguyên tố chung và riêng của 6, 27 và 18 là 2; 3, tương ứng với các số mũ lớn nhất là 1; 3. 

Khi đó: BCNN(6, 27, 18) = 21 . 33 = 2 . 27 = 54

+ 54 : 6 = 9; 54 : 27 = 2; 54 : 18 = 3

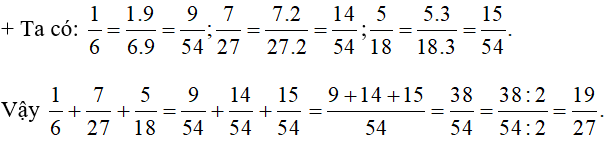
Bài 2. Tìm bội chung nhỏ nhất của:

a) 54 và 108;

b) 21, 30, 70.

Lời giải: 

a) Ta có: 54 = 2 . 27 = 2 . 33 

108 = 4 . 27 = 22 . 33 

Các thừa số nguyên tố chung và riêng của 54 và 108 là 2 và 3, tương ứng với các số mũ lớn nhất lần lượt là 2 và 3

Khi đó: BCNN(54, 108) = 22 . 33 = 4 . 27 = 108.

b) Ta có: 21 = 3 . 7

30 = 3 . 10 = 3 . 2 . 5; 70 = 7. 10 = 7 . 2 . 5

Các thừa số nguyên tố chung và riêng của 21, 30, 70 là 2, 3, 5, 7; chúng đều có số mũ lớn nhất là 1.

Do đó: BCNN(21, 30, 70) = 2 . 3. 5 . 7 = 210.