Lý thuyết Ước chung và ước chung lớn nhất (Cánh diều 2024) Toán 6

Lý thuyết Toán lớp 6 Bài 12: Ước chung và ước chung lớn nhất

Video giải Toán 6 Bài 12: Ước chung và ước chung lớn nhất - Cánh diều

A. Lý thuyết Ước chung và ước chung lớn nhất

I. Ước chung và ước chung lớn nhất 

1. Ước chung: Số tự nhiên n được gọi là ước chung của hai số a và b nếu n vừa là ước của a vừa là ước của b.

Quy ước: Viết tắt ước chung là ƯC.

Kí hiệu: Tập hợp các ước chung của a và b là ƯC(a, b).

Ví dụ: Ta có: 

Các ước của 8 là: 1, 2, 4, 8

Các ước của 12 là: 1, 2, 3, 4, 6, 12

Do đó các ước chung của 8 và 12 là: 1, 2, 4.

Vậy ƯC(8, 12) = {1; 2; 4} .

Chú ý: Số tự nhiên n được gọi là ước chung của ba số a, b, c nếu n là ước của cả ba số a, b, c. 

Ví dụ: Số 14 chia hết cho 7 nên 7 là ước của 14, 21 chia hết cho 7 nên 7 là ước của 21, 49 chia hết cho 7 nên 7 là ước của 49. Vậy 7 là ước chung của ba số 14, 21, 49. 

2. Ước chung lớn nhất: Số lớn nhất trong các ước chung của hai số a và b được gọi là ước chung lớn nhất của a và b.

Quy ước: Viết tắt ước chung lớn nhất là ƯCLN.

Kí hiệu: ước chung lớn nhất của a và b là ƯCLN(a, b). 

Ví dụ: Trong các ước chung của 8 và 12 là 1, 2, 4 thì 4 là số lớn nhất nên 4 là ước chung lớn nhất của 8 và 12. Ta viết ƯCLN(8, 12) = 4.

3. Tìm ước chung của hai số khi biết ƯCLN của hai số đó

Ước chung của hai số là ước của ước chung lớn nhất của chúng. 

Ví dụ: Biết ƯCLN (a, b) = 60. Tìm tất cả các số có hai chữ số là ước chung của a và b.

Lời giải:

Vì ước chung của a và b đều là ước của ƯCLN (a, b) = 60 nên tất cả các số có hai chữ số là ước chung của a và b là: 10, 12, 15, 20, 30, 60.

II. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố

Các bước tìm ƯCLN bằng cách phân tích ra thừa số nguyên tố:

Bước 1. Phân tích mỗi số ra thừa số nguyên tố

Bước 2. Chọn ra các thừa số nguyên tố chung

Bước 3. Với mỗi thừa số nguyên tố chung, ta chọn lũy thừa với số mũ nhỏ nhất

Bước 4. Lấy tích của các lũy thừa đã chọn, ta nhận được ước chung lớn nhất cần tìm.

Ví dụ: Tìm ƯCLN(54, 90).

+ Phân tích các số ra thừa số nguyên tố

54 = 2.33

90 = 2.32.5

Thừa số nguyên tố chung là 2 và 3. Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 3 là 2.

Vậy ƯCLN (54, 90) = 2.32 = 18.

Chú ý: 

+ Nếu hai số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1.

+ Nếu 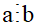  thì ƯCLN(a, b) = b. Chẳng hạn, ƯCLN(48, 16) = 16.

III. Hai số nguyên tố cùng nhau

1. Hai số nguyên tố cùng nhau

Hai số nguyên tố cùng nhau là hai số có ước chung lớn nhất bằng 1.

Ví dụ: Hai số 14 và 33 là hai số nguyên tố cùng nhau vì ƯCLN(14, 33) = 1. 

2. Phân số tối giản

+ Phân số tối giản là phân số có tử và mẫu là hai số nguyên tố cùng nhau.

Ví dụ: Ta có: ƯCLN(4, 9) = 1 nên phân số 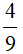là phân số tối giản.  

+ Ta có thể rút gọn một phân số về phân số tối giản bằng cách chia cả tử và mẫu của phân số đó cho ƯCLN của chúng. 

Ví dụ: Rút gọn phân số 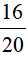  về phân số tối giản.

Ta có: ƯCLN(16, 20) = 4. Vậy  .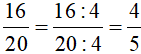

B. Bài tập tự luyện

Bài 1. Một căn phòng hình chữ nhật có chiều dài là 680 cm và chiều rộng là 480 cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch đó có độ dài lớn nhất bằng bao nhiêu?

Lời giải: 

Gọi độ dài của viên gạch hình vuông là x  .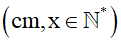

Để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì x phải là ước chung của chiều dài và chiều rộng.

Hay 680 ⋮ x và 480 ⋮ x 

Do đó x ∈ ƯC(680, 480)

Để x lớn nhất thì x = ƯCLN(680, 480)

Ta có: 680 = 23 . 5 . 17; 480 = 25 . 3 . 5 

Khi đó: x = ƯCLN(680, 480) = 23 . 5 = 40.

Vậy để lát kín căn phòng đó mà không có viên gạch nào bị cắt xén thì độ dài lớn nhất của viên gạch là 40 cm. 

Bài 2. Tìm ƯCLN(126, 150). Từ đó hãy tìm tất cả các ước chung của 126 và 150.

Lời giải: 

+ Ta có: 

Do đó: 126 = 2 . 3 . 3 . 7 = 2 . 32 . 7

150 = 2 . 3 . 5 . 5 = 2 . 3 . 52

Các thừa số nguyên tố chung của 126 và 150 là 2 và 3

Số 2 có số mũ nhỏ nhất là 1; số 3 có số mũ nhỏ nhất là 1.

Do đó: ƯCLN(126, 150) = 21 . 31 = 2 . 3 = 6 

Lại có 6 có các ước là 1; 2; 3; 6.

Ước chung của 126 và 150 là ước của ƯCLN(126, 150) là 1; 2; 3; 6

Hay ƯC(126, 150) =  

Vậy ƯCLN(126, 150) = 6; ƯC(126, 150) = . 

Bài 3. Rút gọn phân số 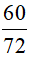  về phân số tối giản.

Lời giải: 

Các phân số được gọi là tối giản khi phân số đó có tử và mẫu là hai số nguyên tố cùng nhau. Vậy để rút gọn các phân số (chưa phải là phân số tối giản) thì ta đi tìm ƯCLN của tử số và mẫu số, rồi lấy cả tử và mẫu chia cho ƯCLN của cả hai thì ta được phân số tối giản. 

Rút gọn phân số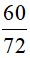   

Ta có: 

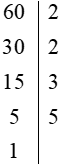
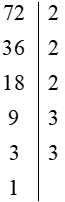
Do đó: 60 = 22 . 3 . 5 và 72 = 23 . 32

Các thừa số nguyên tố chung là 2 và 3, số mũ nhỏ nhất của 2 là 2, số mũ nhỏ nhất của 3 là 1

Suy ra ƯCLN(60, 72) = 22 . 31 = 4 . 3 = 12 

Vậy