Lý thuyết Phân tích một số ra thừa số nguyên tố (Cánh diều 2024) Toán 6

Lý thuyết Toán lớp 6 Bài 11: Phân tích một số ra thừa số nguyên tố

Video giải Toán 6 Bài 11: Phân tích một số ra thừa số nguyên tố - Cánh diều

A. Lý thuyết Phân tích một số ra thừa số nguyên tố

I. Cách tìm một ước nguyên tố của một số 

Để tìm một ước nguyên tố của số tự nhiên n lớn hơn 1, ta có thể làm như sau: lần lượt thực hiện phép chia n cho các số nguyên tố theo thứ tự tăng dần 2, 3, 5, 7, 11, 13, …

Khi đó, phép chia hết đầu tiên cho ta số chia là một ước nguyên tố của n.

Ví dụ: Tìm một ước nguyên tố của 217.

Lời giải:

Theo dấu hiệu chia hết, số 217 không chia hết cho các số nguyên tố 2, 3, 5. Ta có: 217 = 7 . 31. Vì thế 7 là một ước nguyên tố của 217.

II. Phân tích một số ra thừa số nguyên tố

+ Phân tích một số tự nhiên lớn hơn 1 ta thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

Lưu ý: Khi phân tích một số ra thừa số nguyên tố ta nên chia mỗi số trong khi phân tích cho ước nguyên tố nhỏ nhất của nó.

Cứ tiếp tục chia như thế cho đến khi được thương là 1.

+ Ta có thể phân tích một số ra thừa số nguyên tố bằng cách viết “rẽ nhánh” và “theo cột dọc”. 

Ví dụ: Phân tích số 40 ra thừa số nguyên tố bằng cách viết “rẽ nhánh” và “theo cột dọc”.

Lời giải:

+ Cách viết 'rẽ nhánh':

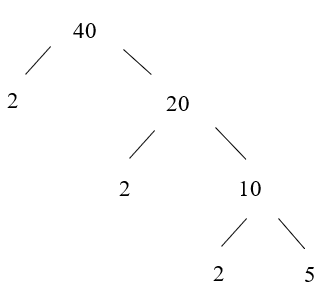
Do đó: 40 = 2 . 2 . 2 . 5 = 23 . 5

+ Cách viết 'theo cột dọc':

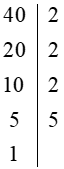
Vậy ta phân tích được: 40 = 2 . 2 . 2 . 5 = 23 . 5. 

Chú ý:

+ Dạng phân tích ra thừa số nguyên tố của một số nguyên tố là chính số đó.

+ Mọi hợp số đều phân tích được ra thừa số nguyên tố.

+ Thông thường, khi phân tích một số tự nhiên ra thừa số nguyên tố, các ước nguyên tố được viết theo thứ tự tăng dần.

+ Ngoài cách làm như trên, ta cũng có thể phân tích một số ra thừa số nguyên tố bằng cách viết số đó thành tích của hai thừa số một cách linh hoạt.

Ví dụ: Phân tích số 450 ra thừa số nguyên tố. 

Ta có: 450 = 9 . 50 

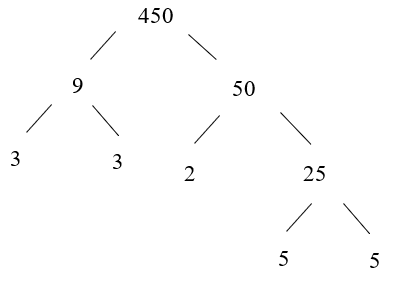
Vậy 450 = 3 . 3 . 2 . 5 . 5 = 2 . 32 . 52. 

Nhận xét: Dù phân tích một số ra thừa số nguyên tố bằng cách nào thì cuối cùng ta cũng được cùng một kết quả.

B. Bài tập tự luyện

Bài 1. 

a) Biết 400 = 24 . 52. Hãy viết 800 thành tích các thừa số nguyên tố.

b) Biết 2 700 = 22 . 33 . 52. Hãy viết 270 và 900 thành tích các thừa số nguyên tố.

Lời giải:

a) Ta có: 800 = 2 . 400 

Mà 400 = 24 . 52 

Do đó: 800 = 2 . (24 . 52) = (21 . 24). 52 = 24+1 . 52 = 25 . 52

Vậy 800 = 25 . 52. 

b) Ta có: 2 700 =  10 . 270 = 3 . 900

Mà 10 = 2 . 5 và 2 700 = 22 . 33 . 52 

Do đó: 270 = 2 700 : 10 = (22 . 33 . 52) : (2 . 5) = (22 : 2) . 33 . (52 : 5) = 2 . 33 . 5

900 = 2 700 : 3 = (22 . 33 . 52) : 3 = 22 . (33 : 3) . 52 = 22 . 32 .52

Vậy 270 = 2 . 33 . 5 và 900 = 22 . 32 .52.

Bài 2. Phân tích các số sau ra thừa số nguyên tố: 45, 270.

Lời giải:

Học sinh có thể phân tích bằng cách viết 'rẽ nhánh' hoặc 'theo cột dọc'.

Có thể trình bày như sau: 

+) Phân tích số 45 bằng cách viết 'theo cột dọc'

Vậy 45 = 3 . 3. 5 = 32 . 5. 

+) Phân tích số 270 bằng cách viết 'rẽ nhánh':

Ta có: 270 = 10 . 27 

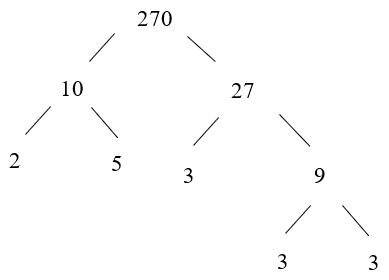
Vậy 270 = 2 . 5 . 3 . 3. 3 = 2 . 33 . 5.