Lý thuyết Hình chữ nhật. Hình thoi (Cánh diều 2024) Toán 6
Tóm tắt lý thuyết Toán 6 Bài 2: Hình chữ nhật. Hình thoi ngắn gọn, chính xác sách Cánh diều sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 6.
Lý thuyết Toán lớp 6 Bài 2: Hình chữ nhật. Hình thoi
A. Lý thuyết Hình chữ nhật. Hình thoi
I. Hình chữ nhật
1. Nhận biết hình chữ nhật
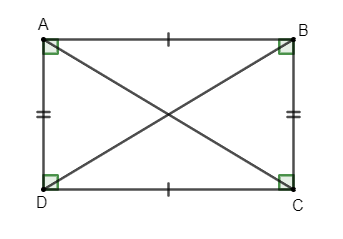
Cho hình chữ nhật ABCD:
Khi đó hình chữ nhật ABCD có:
+ Hai cạnh đối bằng nhau: AB = CD; AD = BC;
+ Hai cạnh đối AB và CD; AD và BC song song với nhau;
+ Hai đường chéo bằng nhau: AC = BD;
+ Bốn góc ở các đỉnh A, B, C, D đều là góc vuông.
2. Vẽ hình chữ nhật
Ta sử dụng ê ke để vẽ hình chữ nhật khi biết độ dài hai cạnh của nó:
Chẳng hạn, vẽ hình chữ nhật ABCD biết AB = 6 cm, AD = 9 cm.
Ta thực hiện các bước như sau:
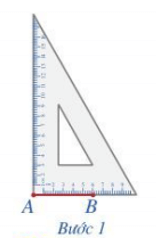
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB = 6 cm.
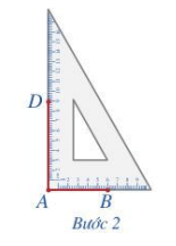
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD = 9 cm.
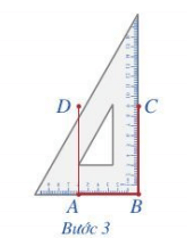
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC = 9 cm.
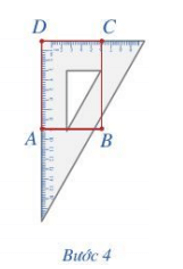
Bước 4. Vẽ đoạn thẳng CD.
Vậy ta có hình chữ nhật ABCD thỏa mãn yêu cầu bài toán.
3. Chu vi và diện tích hình chữ nhật
Hình chữ có độ dài hai cạnh là a và b, ta có:
- Chu vi của hình chữ nhật là: C = 2(a + b);
- Diện tích của hình chữ nhật là: S = a . b.
II. Hình thoi
1. Nhận biết hình thoi
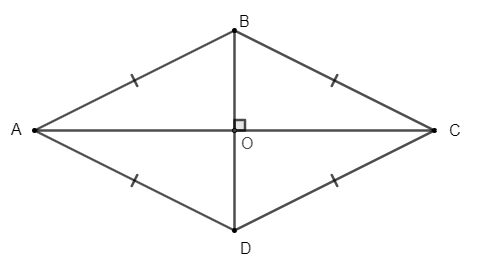
Cho hình thoi ABCD, có hai đường chéo AC và BD cắt nhau tại O.
Khi đó, hình thoi ABCD có:
+ Bốn cạnh bằng nhau: AB = BC = CD = DA;
+ Hai cạnh đối AB và CD, AD và BC song song với nhau;
+ Hai đường chéo AC và BD vuông góc với nhau.
2. Vẽ hình thoi
Ta có thể vẽ được hình thoi khi biết độ dài một cạnh và độ dài một đường chéo bằng thước kẻ và compa.
Chẳng hạn, vẽ hình thoi ABCD biết AB = 5 cm và AC = 8 cm.
Để vẽ hình thoi ABCD, ta làm như sau:
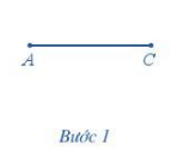
Bước 1. Dùng thước vẽ đoạn thẳng AC = 8 cm
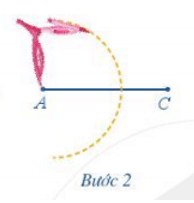
Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính 5 cm
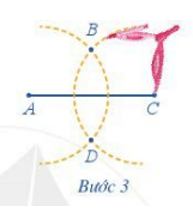
Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính 5 cm; phần đường tròn này cắt phần đường tròn tâm A vẽ ở Bước 2 tại các điểm B và D
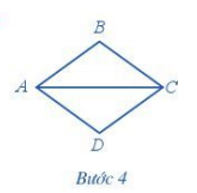
Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA.
Vậy ta được hình thoi ABCD thỏa mãn yêu cầu.
3. Chu vi và diện tích hình thoi
Cho hình thoi có độ dài cạnh là a và độ dài hai đường chéo là m và n, ta có:
- Chu vi của hình thoi là C = 4a;
- Diện tích của hình thoi là S = . m . n.
B. Bài tập tự luyện
Bài 1. Bác Hưng uốn một dây thép thành móc treo đồ có dạng hình thoi với độ dài cạnh bằng 30 cm. Bác Hưng cần bao nhiêu xăng-ti-mét dây thép để làm móc treo đó?
Lời giải:
Độ dài dây thép để làm móc treo chính là chu vi của hình thoi có độ dài cạnh bằng 30 cm.
Do đó bác Hưng cần số xăng-ti-mét dây thép để làm móc treo là:
4 . 30 = 120 (cm)
Vậy bác Hưng cần số xăng-ti-mét dây thép để làm móc treo là 120 cm.
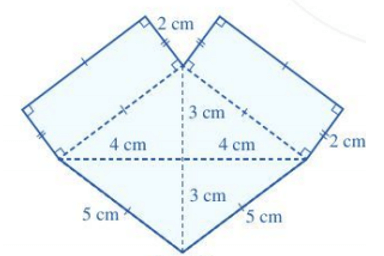
Bài 2. Quan sát hình dưới và tính diện tích phần tô màu xanh ở hình đó.
Lời giải:
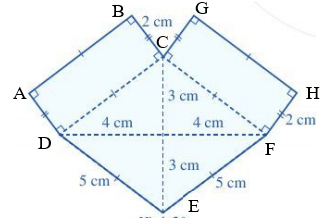
Kí hiệu trên hình vẽ đã cho, các điểm đỉnh như hình dưới đây:
Khi đó, theo kí hiệu trên hình vẽ ta thấy:
AB = CD = CF = GH = DE = EF = 5 cm
AD = BC = CG = HF = 2 cm
CE = 3 + 3 = 6 cm
DF = 4 + 4 = 8 cm
Vì CD = DE = EF = CF nên CDEF là hình thoi với CE và DF là hai đường chéo
Diện tích hình thoi CDEF là: (cm2)
Ta thấy ABCD và CGHF là hai hình chữ nhật có diện tích bằng nhau và có độ dài hai cạnh ở mỗi hình lần lượt là 2 cm và 5 cm.
Diện tích hình chữ nhật ABCD (hay CGHF) là: 2 . 5 = 10 (cm2)
Ta thấy diện tích phần tô màu xanh chính bằng tổng diện tích 2 hình chữ nhật ABCD, CGHF và diện tích hình thoi CDEF.
Do đó, diện tích phần tô màu xanh trên Hình 20 là:
24 + 10 . 2 = 44 (cm2)
Vậy diện tích phần tô màu xanh trên Hình 20 là 44 cm2.