Lý thuyết Quan hệ chia hết. Tính chất chia hết (Cánh diều 2024) Toán 6

Lý thuyết Toán lớp 6 Bài 7: Quan hệ chia hết. Tính chất chia hết

Video giải Toán 6 Bài 7: Quan hệ chia hết. Tính chất chia hết  - Cánh diều

A. Lý thuyết Quan hệ chia hết. Tính chất chia hết

I. Quan hệ chia hết

1. Khái niệm về chia hết

Cho hai số tự nhiên a và b (b # 0) .

Nếu có số tự nhiên q sao cho a = b . q thì ta nói a chia hết cho b.

Khi a chia hết cho b, ta nói a là bội của b và b là ước của a.

Ví dụ: 42 = 6 . 7 nên 42 chia hết cho 6. 

Khi đó ta gọi 42 là bội của 6 và 6 là ước của 42. 

Lưu ý: 

+ Nếu số dư trong phép chia a cho b bằng 0 thì a chia hết cho b, kí hiệu là  .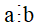

+ Nếu số dư trong phép chia a cho b khác 0 thì a không chia hết cho b, kí hiệu là  .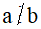

Ví dụ: 

+ 4 chia hết cho 2, kí hiệu là  

+ 5 không chia hết cho 2, kí hiệu là  

Lưu ý: Với a là số tự nhiên khác 0 thì:

+ a là ước của a;

+ a là bội của a;

+ 0 là bội của a;

+ 1 là ước của a.

Ví dụ: 

0 và 7 là hai bội của 7.

1 và 12 là hai ước của 12.

2. Cách tìm bội và ước của một số

2.1 Cách tìm bội của một số 

Để tìm các bội của n(n∈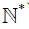) ta có thể lần lượt nhân n với 0, 1, 2, 3, …. Khi đó, các kết quả nhận được đều là bội của n.

Ví dụ: Tìm các bội nhỏ hơn 20 của 7. 

Lời giải: 

Để tìm các bội của 7 ta lần lượt nhân 7 với 0, 1, 2, 3,… ta được 0, 7, 14, 21,…

Các bội của 7 là: 0, 7, 14, 21,…

Mà cần tìm các bội của 7 nhỏ hơn 20 nên các số thỏa mãn yêu cầu là 0, 7, 14. 

Vậy các bội nhỏ hơn 20 của 7 là 0, 7, 14.  

2.2 Cách tìm ước của một số 

Để tìm các ước của số tự nhiên n lớn hơn 1 ta có thể lần lượt chia n cho các số tự nhiên từ 1 đến n. Khi đó, các phép chia hết cho ta số chia là ước của n.

Ví dụ: Tìm các ước của 15.

Lời giải: 

Thực hiện phép chia số 15 cho lần lượt các số tự nhiên từ 1 đến 15. Các phép chia hết là: 15 : 1 = 15; 15 : 3 = 5; 15 : 5 = 3; 15 : 15 = 1.

Vì vậy, các ước của 15 là 1, 3, 5, 15.

II. Tính chất chia hết

1. Tính chất chia hết của một tổng

Tổng quát: Nếu tất cả các số hạng của tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

Cụ thể đối với tổng 2 số hạng: 

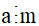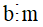Nếu  và thì  .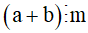

Khi đó ta có: (a + b) : m = a : m + b : m.

Ví dụ: 

+ Ta có: 4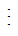2 và 6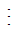2 thì (6 + 4)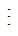2.

Khi đó:  (4 + 6) : 2 = 4 : 2 + 6 : 2. 

+ Ta có: 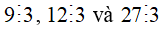thì .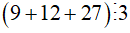

Khi đó:  ( 9 + 12 + 27) : 3 = 9 : 3 + 12 : 3 + 27 : 3

2. Tính chất chia hết của một hiệu

Tổng quát: Nếu số bị trừ và số trừ đều chia hết cho cùng một số thì hiệu chia hết cho số đó.

Cụ thể:

Với a ≥ b :

Nếu 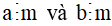thì  .

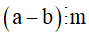Khi đó ta có: (a – b) : m = a : m – b : m.

Ví dụ: Ta có: 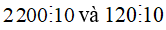thì .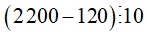

Khi đó: (2200 - 120) :10 =2200 : 10 -120:10 .

3. Tính chất chia hết của một tích

Tổng quát: Nếu một thừa số của tích chia hết cho một số thì tích chia hết cho số đó.

Cụ thể: Nếu 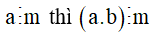 với mọi số tự nhiên b.

Ví dụ: Ta thấy 50 chia hết cho 5 nên tích 50 . 2016 chia hết cho 5. 

B. Bài tập tự luyện

Bài 1. Không tính giá trị biểu thức, hãy giải thích tại sao A = 36 . 234 + 217 . 24 – 54 . 13 chia hết cho 6.

Lời giải: 

Ta có: 36 : 6 = 6;   24 : 6 = 4;    54 : 6 = 9.

Nên các số 36; 24; 54 đều là các số chia hết cho 6, áp dụng tính chất chia hết của một tích ta có:

36 . 234;      217 . 24;       54 . 13 đều là các tích chia hết cho 6.

Khi đó: A = 36 . 234 + 217 . 24 – 54 . 13 chia hết cho 6.

(Theo tính chất chia hết của một tổng và tính chất chia hết của một hiệu).

Bài 2. 

a) Tìm các bội nhỏ hơn 40 của 9.

b) Tìm tất cả các ước của 25. 

Lời giải: 

 a) Để tìm các bội của 9, ta lần lượt nhân 9 với các số 0, 1, 2, 3, 4, 5,… được 0, 9, 18, 27, 36, 45,…

Các bội của 9 là 0, 9, 18, 27, 36, 45,…

Vì cần tìm các bội nhỏ hơn 40 của 9 nên các số thỏa mãn yêu cầu là: 0, 9, 18, 27, 36.

Vậy các bội nhỏ hơn 40 của 9 là: 0, 9, 18, 27, 36. 

b) Để tìm các ước của 25, ta thực hiện phép chia 25 cho các số tự nhiên từ 1 đến 25. Các phép chia hết là: 25 : 1 = 25; 25 : 5 = 5; 25 : 25 = 1 

Vậy các ước của 25 là 1, 5 và 25.