Lý thuyết Phép tính lũy thừa với số mũ tự nhiên (Cánh diều 2024) Toán 6

Lý thuyết Toán lớp 6 Bài 5: Phép tính lũy thừa với số mũ tự nhiên

Video giải Toán 6 Bài 5: Phép tính lũy thừa với số mũ tự nhiên - Cánh diều

A. Lý thuyết Phép tính lũy thừa với số mũ tự nhiên

I. Phép nâng lên lũy thừa 

Lũy thừa bậc n của a, kí hiệu  , là tích của n thừa số a:

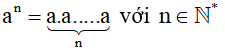
Trong đó:

a được gọi là cơ số

           n được gọi là số mũ.

Quy ước:   a1=a

Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa.

Chú ý: 

+ an  đọc là “a mũ n” hoặc “a lũy thừa n” hoặc “lũy thừa bậc n của a”.

+ a2  còn được gọi là “a bình phương” hay “bình phương của a”.

+ a3 còn được gọi là “a lập phương” hay “lập phương của a”.

Ví dụ: 

7 . 7 . 7 . 7 = 74 (đọc là 7 mũ 4 hoặc là 7 lũy thừa 4, hoặc lũy thừa bậc bốn của 7)

16 = 2 . 2 . 2 . 2 = 24 

Lưu ý: Với n là số tự nhiên khác 0, ta có: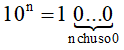 

Ví dụ: 105 = 10 . 10 . 10 . 10 . 10 = 100 000  

II. Nhân hai lũy thừa cùng cơ số

Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: 

am . an = am + n 

Ví dụ: 

+) 23 . 24 = 23 + 4 = 27

+) a2 . a1 = a2 + 1 = a3

+) 42 . 45 = 42 + 5 = 47

III. Chia hai lũy thừa cùng cơ số 

Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ:

am : an = am - n  (a # 0, m ≥ n)

Quy ước: a0 = 1 (a # 0) . 

Ví dụ:
 + 97 : 93 = 97 - 3 = 94

+ 76 : 7 = 76 : 71 = 76 - 1 = 75

+ 33 : 33 = 33 - 3 = 30 = 1

B. Bài tập tự luyện 

Bài 1. So sánh

a) 22 . 23 và 26;     

b) 32 và 23;

c) 52 và 5 . 2.

Lời giải:

a) Ta có: 22 . 23 = 22 + 3 = 25

Vì 5 < 6 nên 25 < 26

Vậy 22 . 23 < 26.

b) Ta có: 32 = 3 . 3 = 9; 23 = 2 . 2 . 2 = 8

Vì 8 < 9 nên 23 < 32 hay 32 > 23 

Vậy 32 > 23.

c) Ta có: 52 = 5 . 5 = 25 

5 . 2 = 10

Vì 25 > 10 nên 52 > 5 . 2

Vậy 52 > 5 . 2. 

Bài 2. Thực hiện các phép tính:

a) 37 . 27 . 81;

b) 100 . 1 000 . 10 000;

c) 1254 : 58.

Lời giải:

a) Ta có: 37 . 27 . 81 = 37.(3.3.3).(3.3.3.3) = 37 . 33 . 34 = 37 + 3 + 4 = 314

b) Ta có: 100 . 1 000 . 10 000 = (102) . (103) . (104) = 102 + 3 + 4 = 109

c) Ta có:

1254 : 58 = (5.5.5)4 : 58 = (53)4 : 58 = [53.53.53.53] : 58

= 53 + 3 + 3 + 3 : 58 = 512 : 58 = 512 - 8 = 54.