Câu hỏi:
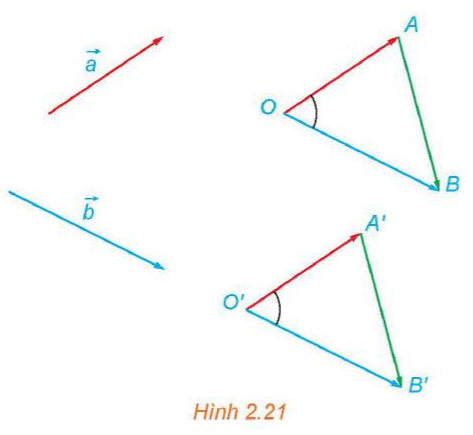
157 lượt xemTrong không gian, cho hai vectơ và không cùng phương. Lấy điểm A và vẽ các vectơ . Lấy điểm A’ và vẽ các vectơ (H.2.10).
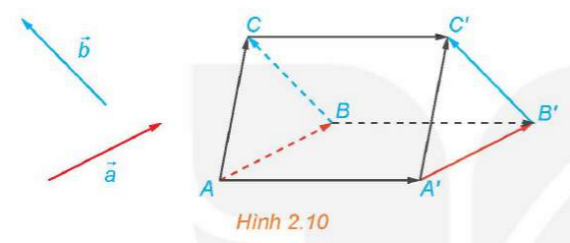
a) Giải thích vì sao và .
b) Giải thích vì sao AA’C’C là hình bình hành, từ đó suy ra .
Lời giải
Hướng dẫn giải:
a) Vì nên hai vectơ và cùng hướng và cùng độ dài.
Vì nên hai vectơ và cùng hướng và cùng độ dài.
Do đó, hai vectơ và cùng hướng và cùng độ dài. Suy ra, AB//A’B’ và . Do đó, tứ giác ABB’A’ là hình bình hành. Suy ra, AA’//BB’ và hai vectơ có cùng hướng và cùng độ dài. Suy ra, .
Vì nên hai vectơ và cùng hướng và cùng độ dài.
Vì nên hai vectơ và cùng hướng và cùng độ dài.
Do đó, hai vectơ và cùng hướng và cùng độ dài. Suy ra, BC//B’C’ và . Do đó, tứ giác CBB’C’ là hình bình hành. Suy ra, CC’//BB’ và hai vectơ có cùng hướng và cùng độ dài. Suy ra, .
b) Vì hai vectơ có cùng hướng và cùng độ dài; hai vectơ có cùng hướng và cùng độ dài nên hai vectơ và có cùng hướng và cùng độ dài. Do đó, AA’//CC’ và nên tứ giác AA’C’C là hình bình hành. Suy ra, và AC//A’C’. Do đó, hai vectơ có cùng hướng và cùng độ dài. Suy ra, .
Nếu hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó có bằng nhau không?
Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lên tầng 29. Các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau không? Giải thích vì sao.

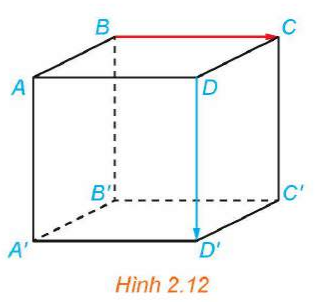
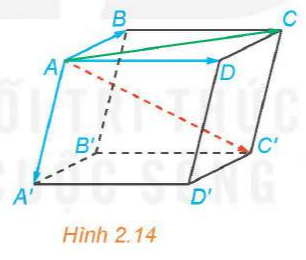
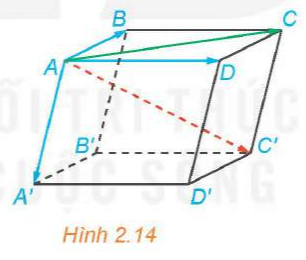
Trong Hình 2.14, hãy phát biểu quy tắc hình hộp với các vectơ có điểm đầu là B.
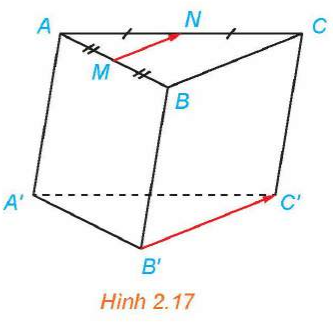
Trong Ví dụ 8, gọi I là điểm thuộc đoạn thẳng AG sao cho (H.2.19). Chứng minh rằng .
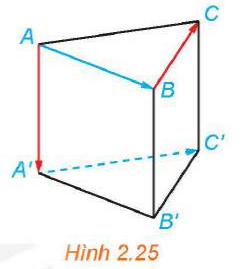
Cho hình lăng trụ tam giác đều ABC.A’B’C’ (H.2.25). Tính các góc và .
Hãy nhắc lại công thức xác định tích vô hướng của hai vectơ trong mặt phẳng.
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có và . Tính độ dài của các vectơ và .