Giải Toán 10 trang 67 Tập 1

Câu hỏi trang 67 Toán 10 Tập 1: Khi nào tích vô hướng của hai vectơ khác vectơ-không $\overrightarrow{u},\overrightarrow{v}$ là một số dương? Là một số âm?

Luyện tập 1 trang 66 Toán 10 Tập 1: Cho tam giác đều ABC. Tính $\left(\overrightarrow{AB},\overrightarrow{BC}\right).$

Câu hỏi trang 66 Toán 10 Tập 1: Khi nào thì góc giữa hai vectơ bằng 0°, bằng 180°.

Giải bài tập Toán 10 Bài 11: Tích vô hướng của hai vecto

1. Góc giữa hai vecto

Giải Toán 10 trang 66 Tập 1

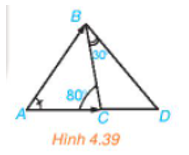
HĐ 1 trang 66 Toán 10 Tập 1: Trong Hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$. Hãy tìm số đo các góc giữa $\overrightarrow{BC}$ và $\overrightarrow{BD}$, $\overrightarrow{DA}$ và $\overrightarrow{DB}$.

Bài 4.20 trang 65 Toán 10 Tập 1: Trong Hình 4.38, quân mã đang vị trí có tọa độ (1;2). Hỏi sau một nước đi, quân mã có thể đến những vị trí nào?

Bài 4.19 trang 65 Toán 10 tập 1: Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(1;2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vectơ $\overrightarrow{v}=\left(3;4\right).$ Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.

Bài 4.18 trang 65 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;3), B(2;4), C(‒3;2).

a) Chứng minh rằng ABC là ba đỉnh của một tam giác.

b) Tìm tọa độ trung điểm M của đoạn thẳng AB.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tìm điểm D(x; y) để O(0;0) là trọng tâm tam giác ABD.

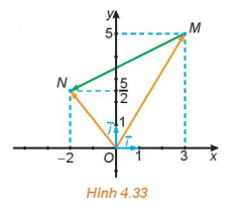
Bài 4.17 trang 65 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các vectơ $\overrightarrow{a}=3\overrightarrow{i}-2\overrightarrow{j};$$\overrightarrow{b}=\left(4;-1\right)$ và các điểm M(‒3;6), N(3;‒3).

a) Tìm mối liên hệ giữa các vectơ $\overrightarrow{MN}$ và $2\overrightarrow{a}-\overrightarrow{b}.$

b) Các điểm O, M, N có thẳng hàng hay không?

c) Tìm điểm P(x;y) để OMNP là hình bình hành.

Bài tập

Giải Toán 10 trang 65 Tập 1

Bài 4.16 trang 65 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2).

a) Tính độ dài của các đoạn thẳng OM, ON, MN.

b) Chứng minh rằng tam giác OMN vuông cân.

Giải Toán 10 trang 64 Tập 1

Vận dụng trang 64 Toán 10 Tập 1: Từ thông tin dự báo bão được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ dự báo.

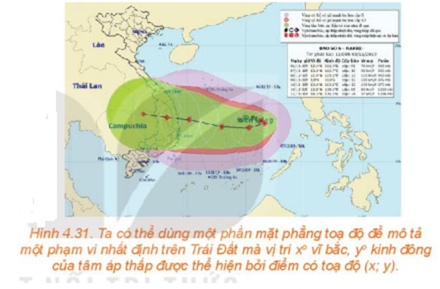
Trong 12 giờ, tâm bão được dự báo di chuyển thẳng đều từ A(13,8; 108,3) tới vị trí có tọa độ B(14,1; 106,3). Gọi tọa độ của M là (x;y). Bạn hãy tìm mối liên hệ giữa hai vectơ $\overrightarrow{AM}$ và $\overrightarrow{AB}$ rồi thể hiện mối quan hệ đó theo tọa độ để tìm x; y.

Giải Toán 10 trang 63 Tập 1

Luyện tập 2 trang 63 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3).

a) Các điểm O, A, B có thẳng hàng hay không?

b) Tìm điểm M(x;y) để OABM là một hình bình hành.

HĐ 5 trang 62 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M(x; y) và N(x'; y').

a) Tìm tọa độ của các vectơ $\overrightarrow{OM},\overrightarrow{ON}$.

b) Biểu thị vectơ $\overrightarrow{MN}$ theo các vectơ $\overrightarrow{OM},\overrightarrow{ON}$ và tìm tọa độ của $\overrightarrow{MN}$

c) Tìm độ dài của vectơ $\overrightarrow{MN}$

Giải Toán 10 trang 62 Tập 1

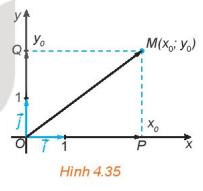
HĐ 4 trang 62 Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy, cho điểm M(x0;y0).

Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35).

a) Trên trục Ox, điểm P biểu diễn số nào? Biểu thị $\overrightarrow{OP}$  theo $\overrightarrow{i}$và tính độ dài của $\overrightarrow{OP}$ theo x0.

b) Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị $\overrightarrow{OQ}$ theo $\overrightarrow{j}$ và tính độ dài của $\overrightarrow{OQ}$ theo y0.

c) Dựa vào hình chữ nhật OPMQ, tính độ dài của $\overrightarrow{OM}$ theo x0, y0.

d) Biểu thị $\overrightarrow{OM}$ theo các vectơ $\overrightarrow{i},\overrightarrow{j}$.

2. Biểu thức tọa độ của các phép toán vecto

HĐ 3 trang 61 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{u}=\left(2;-3\right),\overrightarrow{v}=\left(4;1\right),\overrightarrow{a}=\left(8;-12\right).$

a) Hãy biểu thị mỗi vectơ $\overrightarrow{u},\overrightarrow{v},\overrightarrow{a}$ theo các vectơ $\overrightarrow{i},\overrightarrow{j}.$

b) Tìm tọa độ của các vectơ $\overrightarrow{u}+\overrightarrow{v},4\overrightarrow{u}.$

c) Tìm mối liên hệ giữa hai vectơ $\overrightarrow{u},\overrightarrow{a}.$

Luyện tập 1 trang 61 Toán 10 Tập 1: Tìm tọa độ của $\overrightarrow{0}$.

Giải Toán 10 trang 61 Tập 1

HĐ 2 trang 61 Toán 10 Tập 1: Trong Hình 4.33:

a) Hãy biểu thị mỗi vectơ $\overrightarrow{OM},\overrightarrow{ON}$ theo các vectơ $\overrightarrow{i},\overrightarrow{j}$.

b) Hãy biểu thị vectơ $\overrightarrow{MN}$ theo các vectơ $\overrightarrow{OM},\overrightarrow{ON}$ từ đó biểu thị vectơ $\overrightarrow{MN}$ theo các vectơ $\overrightarrow{i},\overrightarrow{j}$.

1. Tọa độ của Vecto

Giải Toán 10 trang 60 Tập 1

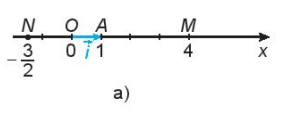
HĐ 1 trang 60 Toán 10 Tập 1: Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt $\overrightarrow{OA}=\overrightarrow{i}$ (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số $-\frac{3}{2}.$ Hãy biểu thị mỗi vectơ $\overrightarrow{OM},\overrightarrow{ON}$ theo vectơ đơn vị $\overrightarrow{i}.$

Giải bài tập Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ

Mở đầu

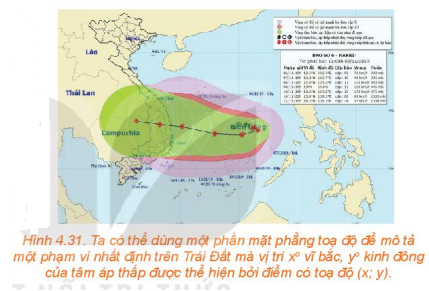
Mở đầu trang 60 Toán 10 Tập 1: Một bản tin dự báo thời tiết thể hiện đường đi trong 12 giờ của một cơn bão trên một mặt phẳng tọa độ. Trong thời gian đó, tâm bão di chuyển thẳng đều từ vị trí có tọa độ (13,8; 108,3) đến vị trí tọa độ (14,1; 106,3). Dựa vào thông tin trên, liệu ta có thể dự đoán được vị trí của tâm bão tại thời điểm bất kì trong khoảng thời gian 12 giờ đó hay không?

Giải Toán 10 trang 59 Tập 1

Bài 4.15 trang 59 Toán 10 Tập 1: Chất điểm A chịu tác động của ba lực $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$ như Hình 4.30 và ở trạng thái cân bằng (tức là $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{0}$). Tính độ lớn của các lực $\overrightarrow{F_2},\overrightarrow{F_3},$ biết $\overrightarrow{F_1},$ có độ lớn là 20 N.

Bài 4.14 trang 58 Toán 10 Tập 1: Cho tam giác ABC.

a) Hãy xác định điểm M để $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}.$

b) Chứng minh rằng với mọi điểm O, ta có: $\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}=4\overrightarrow{OM}.$

Bài 4.13 trang 58 Toán 10 Tập 1: Cho hai điểm phân biệt A và B.

a) Hãy xác định điểm K sao cho $\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{0}.$

b) Chứng minh rằng với mọi điểm O, ta có: $\overrightarrow{OK}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}.$

Bài 4.12 trang 58 Toán 10 Tập 1: Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng $\overrightarrow{BC}+\overrightarrow{AD}=2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}.$

Bài tập

Giải Toán 10 trang 58 Tập 1

Bài 4.11 trang 58 Toán 10 Tập 1: Cho hình bình hành ABCD. Gọi M là trung điểm cạnh BC. Hãy biểu thị $\overrightarrow{AM}$ theo hai vecto $\overrightarrow{AB}$ và $\overrightarrow{AD}$

Luyện tập 3 trang 57 Toán 10 Tập 1: Trong Hình 4.27, hãy biểu thị mỗi vectơ $\overrightarrow{u},\overrightarrow{v}$ theo hai vectơ $\overrightarrow{a},\overrightarrow{b}$, tức là tìm các số x, y, z, t để $\overrightarrow{u}=x\overrightarrow{a}+y\overrightarrow{b},\overrightarrow{v}=t\overrightarrow{a}+z\overrightarrow{b}.$

Luyện tập 2 trang 57 Toán 10 Tập 1: Cho tam giác ABC có trọng tâm G. Chứng minh với điểm O tùy ý, ta có:

$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}$

HĐ 4 trang 57 Toán 10 Tập 1: Hãy chỉ ra trên Hình 4.26 hai vectơ $3\left(\overrightarrow{u}+\overrightarrow{v}\right)$ và $3\overrightarrow{u}+3\overrightarrow{v}$. Từ đó, nêu mối quan hệ giữa $3\left(\overrightarrow{u}+\overrightarrow{v}\right)$ và $3\overrightarrow{u}+3\overrightarrow{v}$.

2. Các tính chất của phép nhân vecto với 1 số 

Giải Toán 10 trang 57 Tập 1

HĐ 3 trang 57 Toán 10 Tập 1: Với $\overrightarrow{u}\ne \overrightarrow{0}$ và hai số thực k, t, những khẳng định nào sau đây là đúng?

a) Hai vectơ $k\left(t\overrightarrow{u}\right)$ và $\left(kt\right)\overrightarrow{u}$ có cùng độ dài bằng $\left|kt\right|\left|\overrightarrow{u}\right|.$

b) Nếu kt ≥ 0 thì cả hai vectơ $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$ cùng hướng với $\overrightarrow{u}$.

c) Nếu kt < 0 thì cả hai vectơ $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$ ngược hướng với $\overrightarrow{u}$.

d) Hai vectơ $k\left(t\overrightarrow{u}\right)$ và $\left(kt\right)\overrightarrow{u}$ bằng nhau.

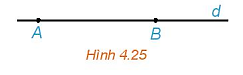
Luyện tập 1 trang 56 Toán 10 Tập 1: Cho đường thẳng d đi qua hai điểm phân biệt A và B (H.4.25). Những khẳng định nào sau đây là đúng?

a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để $\overrightarrow{AM}=t\overrightarrow{AB}$.

b) Với điểm M bất kì, ta luôn có: $\overrightarrow{AM}=\frac{AM}{AB}.\overrightarrow{AB}.$

c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số t ≤ 0 để $\overrightarrow{AM}=t\overrightarrow{AB}.$

Câu hỏi trang 56 Toán 10 Tập 1: $-\overrightarrow{a}$ và $(-1)\overrightarrow{ a}$ có mối quan hệ gì?

Giải Toán 10 trang 56 Tập 1

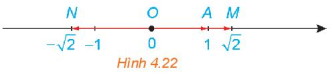
HĐ 2 trang 56 Toán 10 Tập 1: Trên một trục số, gọi O, A, M, N tương ứng biểu diễn các số $0;1;\sqrt{2};-\sqrt{2}.$Hãy nêu mối quan hệ về hướng và độ dài của mỗi vecto $\overrightarrow{OM},\overrightarrow{ON}$với vecto $\overrightarrow{a}=\overrightarrow{OA}$. Viết đẳng thức thể hiện mối quan hệ giữa hai vecto $\overrightarrow{OM}$và $\overrightarrow{OA}$.

Câu hỏi trang 55 Toán 10 Tập 1: $1\overrightarrow{a}$ và $\overrightarrow{a}$ có bằng nhau hay không?

1. Tích của một vecto với một số

Giải Toán 10 trang 55 Tập 1

HĐ 1 trang 55 Toán 10 Tập 1: Cho vecto $\overrightarrow{AB}=\overrightarrow{a}$. Hãy xác định điểm C sao cho $\overrightarrow{BC}=\overrightarrow{a}.$

a) Tìm mối quan hệ giữa $\overrightarrow{AB}$ và $\overrightarrow{a}+\overrightarrow{a}.$

b) Vecto $\overrightarrow{a}+\overrightarrow{a}$ có mối quan hệ như thế nào về hướng và độ dài với vecto $\overrightarrow{a}.$

Giải bài tập Toán 10 Bài 9: Tích của một vecto với một số

Mở đầu

Mở đầu trang 55 Toán 10 Tập 1: Với mỗi cặp vật đặt trên hai đầu của một cánh tay đòn AB, luôn có duy nhất một điểm M thuộc AB để nếu đặt trụ đỡ tại M thì cánh tay đòn ở trạng thái cân bằng (H.4.20). Điều trên còn đúng trong trường hợp tổng quát hơn, chẳng hạn, cánh tay đòn được thay bởi một tấm ván hình đa giác n đỉnh A1, A2, A3, …, An, tại mỗi đỉnh Ai có đặt một vật nặng mi (kg). Ở đây, ta coi cánh tay đòn, tấm ván là không có trọng lượng. Trong Vật lí, điểm M như trên được gọi là điểm khối tâm của hệ chất điểm A1, A2, A3, …, An ứng với các khối lượng m1, m2, m3, …, mn (kg).

Qua bài học này, ta sẽ thấy Hình học cho phép xác định vị trí khối tâm của một hệ chất điểm.

Bài 4.10 trang 54 Toán 10 Tập 1: Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng không đổi và có độ lớn bằng nhau. Hai tàu luôn giữ được lái sao cho chúng tạo với bờ cùng một  góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận tốc dòng nước là đáng kể, các yếu tố bên ngoài khác không ảnh hưởng tới vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước?

Bài 4.9 trang 54 Toán 10 Tập 1: Hình 4.19 biểu diễn hai lực $\overrightarrow{F_1},\overrightarrow{F_2}$ cùng tác động lên một vật, cho $\left|\overrightarrow{F_1}\right|=3N,\left|\overrightarrow{F_2}\right|=2N.$ Tính độ lớn của hợp lực $\overrightarrow{F_1}+\overrightarrow{F_2}$.

Bài 4.8 trang 54 Toán 10 Tập 1: Cho tam giác đều ABC có cạnh bằng a. Tính độ dài các vectơ $\overrightarrow{AB}-\overrightarrow{AC},\overrightarrow{AB}+\overrightarrow{AC}$.

Bài 4.7 trang 54 Toán 10 Tập 1: Cho hình bình hành ABCD. Hãy tìm điểm M để $\overrightarrow{BM}=\overrightarrow{AB}+\overrightarrow{AD}$. Tìm mối quan hệ giữa hai vecto $\overrightarrow{CD}$ và $\overrightarrow{CM}$.

Bài tập

Bài 4.6 trang 54 Toán 10 Tập 1: Cho bốn điểm A, B, C, D. Chứng minh rằng:

a) $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{0};$

b) $\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{BC}-\overrightarrow{BD};$

Giải Toán 10 trang 54 Tập 1

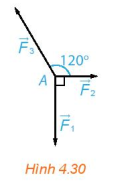
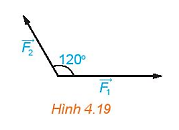
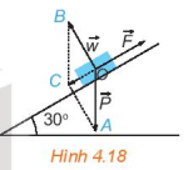
Vận dụng trang 54 Toán 10 Tập 1: Tính lực kéo cần thiết để kéo một khẩu pháo có trọng lượng 22 148N (ứng với khối lượng xấp xỉ 2 260kg) lên một con dốc nghiêng 30° so với phương nằm ngang (H.4.18). Nếu lực kéo của mỗi người bằng 100 N thì cần tối thiểu bao nhiêu người để kéo pháo?

Chú ý: Ta coi khẩu pháo chịu tác động của ba lực: trọng lực $\overrightarrow{P}$ (có độ lớn $\left|\overrightarrow{P}\right|=22148N,$ có phương vuông góc với phương nằm ngang và hướng xuống dưới), phản lực $\overrightarrow{\text{W}}$ (có độ lớn $\left|\overrightarrow{\text{W}}\right|=\left|\overrightarrow{P}\right|cos30°$, có phương vuông góc với mặt dốc và hướng lên trên) và lực kéo $\overrightarrow{F}$(theo phương dốc, hướng từ chân dốc lên đỉnh dốc).

Giải Toán 10 trang 53 Tập 1

Luyện tập 2 trang 53 Toán 10 Tập 1: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của MN. Chứng minh rằng $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$.