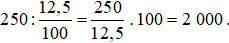30 câu Trắc nghiệm Bài toán về tỉ số phần trăm (có đáp án 2024) – Toán 6 Chân trời sáng tạo

Trắc nghiệm Toán lớp 6 Bài 5: Bài toán về tỉ số phần trăm

Phần 1. Trắc nghiệm Bài toán về tỉ số phần trăm

Câu 1: Một người bán xe đạp được lãi 16% so với giá bán thì được lãi bao nhiêu phần trăm so với giá vốn?

A. 18,5%

B. 19,04%

C. 20,8%

D. 22,05%

Trả lời:

Coi giá bán là 100% thì tiền lãi sẽ chiếm 16% giá bán.

Ta có: Giá bán = giá vốn + lãi.

Giá vốn chiếm số phần trăm so với giá bán là:

100% − 16% = 84%

Tiền lãi chiếm số phần trăm so với giá vốn là:

16:84 = 0,1904 = 19,04%

Đáp số: 19,04%

Đáp án cần chọn là : B

Câu 2: Một cửa hàng bán một tấm vải trong 4 ngày. Ngày thứ nhất bán $\frac{1}{6}$ tấm vải và 5m; ngày thứ hai bán 20% số còn lại và 10m; ngày thứ ba bán 25% số còn lại và 9m; ngày thứ tư bán $\frac{1}{3}$ số vải còn lại. Cuối cùng, tấm vải còn lại 13m. Tính chiều dài tấm vải ban đầu.

A.87m

B.78m

C.60

D.38

Trả lời:

Số mét vải của ngày thứ tư khi chưa bán là: $13:\left(1-\frac{1}{3}\right)=\frac{39}{2}\left(m\right)$

Số mét vải của ngày thứ ba khi chưa bán là: $\left(\frac{39}{2}+9\right):\left(1-25\text{\%}\right)=38\left(m\right)$

Số mét vải của ngày thứ hai khi chưa bán là: $\left(38+10\right):\left(1-20\text{\%}\right)=60\left(m\right)$

Số mét vải của ngày đầu tiên khi chưa bán là: $\left(60+5\right):\left(1-\frac{1}{6}\right)=78\left(m\right)$

Vậy lúc đầu tấm vải dài số mét là: 78m.

Đáp án cần chọn là: B

Câu 3: Một người bỏ ra 160000 đồng tiền vốn mua rau, sau khi bán hết số rau người đó người đó thu về 200000 đồng. Hỏi tiền lãi bằng bao nhiêu phần trăm tiền vốn?

A. 2%

B. 20%

C. 25%

D. 80%

Trả lời:

Tiền lãi thu được sau khi bán hết số rau đó là:

200000 – 160000 = 40000 (đồng)

Tỉ số phần trăm giữa tiền lãi và tiền vốn là:

40000 : 160000 = 0,25 = 25%

Đáp số: 25%

Đáp án cần chọn là : C

Câu 4: Trong các công thức sau, công thức nào đúng?

A. Giá bán = giá vốn - lãi

B. Giá bán = giá vốn + lỗ

C. Giá vốn = giá bán + lãi

D. Giá bán = giá vốn + lãi

Trả lời:

Ta có các công thức :

+) Giá bán = giá vốn + lãi;

+) Giá vốn = giá bán – lãi;

+) Lãi = giá bán – giá vốn;

+) Giá bán = giá vốn – lỗ.

Vậy công thức đúng là:

Giá bán = giá vốn + lãi.

Đáp án cần chọn là: D

Câu 5: Một cửa hàng bán tạp hóa cả ngày bán được 7440000 đồng. Nếu tiền bán được tăng thêm 400000 đồng thì tiền lãi sẽ là 1640000 đồng. Hỏi tiền lãi thực sự bằng bao nhiêu phần trăm tiền vốn?

A. 20%

B. 22,04%

C. 24,4%

D. 28%

Trả lời:

Tiền lãi thực sự cửa hàng thu được là:

1640000 – 400000 = 1240000 (đồng)

Tiền vốn là:

7440000 – 1240000 = 6200000 (đồng)

Tỉ số phần trăm của tiền lãi so với tiền vốn là:

1240000 : 6200000 = 0,2 = 20%

Đáp số: 20%.

Đáp án cần chọn là : A

Câu 6: Tìm một số biết $\frac{3}{5}\%$ của nó bằng 0,3.

A.100

B.60

C.30

D.50

Trả lời:

Đổi $\frac{3}{5}\text{\%}=\frac{3}{5}:100=\frac{3}{500}$

Số đó là: $\mathrm{0,3}:\frac{3}{500}=\frac{3}{10}.\frac{500}{3}=50$

Vậy số cần tìm là 50

Đáp án cần chọn là: D

Câu 7: Tỉ số giữa học sinh nam và học sinh nữ là 80%. Tìm số học sinh nam, biết lớp 6A có 36 học sinh?

A.20 học sinh.

B.17 học sinh.

C.19 học sinh.

D.16 học sinh.

Trả lời:

Đổi $80\text{\%}=\frac{4}{5}$ tức là số học sinh nam bằng $\frac{4}{5}$ số học sinh nữ.

Tổng số phần là: 4 + 5 = 9 (phần)

Lớp 6A có số học sinh nam là: 36 : 9 . 4 = 16 (học sinh)

Vậy lớp có 16 học sinh nam.

Đáp án cần chọn là: D

Câu 8: Hiệu của hai số là 21. Biết 37,5% số lớn bằng 0,6 số nhỏ. Hai số đó là

A.56; 35

B.45; 56

C.60; 39

D.56; 45

Trả lời:

Đổi $\mathrm{37,5}\text{\%}=\frac{3}{8};\mathrm{0,6}=\frac{3}{5}$

Tỉ số giữa số lớn và số nhỏ là: $\frac{3}{5}:\frac{3}{8}=\frac{8}{5}$

Hiệu số phần bằng nhau là: 8−5=3 (phần)

Số lớn là: 21 : 3 × 8 = 56

Số nhỏ là: 56 – 21 = 35

Vậy hai số đó là 56; 35

Đáp án cần chọn là: A

Câu 9: Một lớp có chưa đến 50 học sinh. Cuối năm có 30% số học sinh xếp loại giỏi; $\frac{3}{8}$ số học sinh xếp loại khá, còn lại là trung bình. Tính số học sinh trung bình.

A.15 học sinh

B.13 học sinh

C.20 học sinh

D.99 học sinh

Trả lời:

Đổi $30\text{\%}=\frac{3}{10}$

Vì số học sinh phải là số tự nhiên nên phải chia hết cho 10 và 8

BCNN(10,8) = 40 nên số học sinh của lớp là 40

Phân số chỉ số học sinh trung bình là: $1-\frac{3}{10}-\frac{3}{8}=\frac{13}{40}$ (số học sinh)

Số học sinh trung bình là: $40.\frac{13}{40}=13$ (học sinh)

Vậy lớp có 13 học sinh trung bình.

Đáp án cần chọn là: B

Câu 10: Tỉ số của hai số a và b là 120%. Hiệu của hai số đó là 16. Tìm tổng hai số đó.

A.96

B.167

C.150

D.176

Trả lời:

Đổi $120\text{\%}=\frac{120}{100}=\frac{6}{5}$

Hiệu số phần bằng nhau là: 6 – 5 = 1 (phần)

Số lớn là: 16 : 1.6 = 96

Số bé là: 16 : 1.5 = 80

Tổng hai số là: 96 + 80 = 176

Đáp án cần chọn là: D

Phần 2. Lý thuyết Bài toán về tỉ số phần trăm

1. Tìm giá trị phần trăm của một số

Muốn tìm giá trị a% của số b, ta tính: .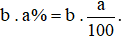

Ví dụ 1. 22,5% của 34 là: .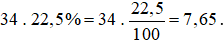

2. Tìm một số khi biết giá trị phần trăm của số đó

Muốn tìm số b khi biết a% của b là c, ta tính: .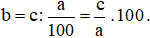

Ví dụ 2. Số có giá trị 12,5% bằng 250 là: