30 câu Trắc nghiệm Số nguyên tố, Hợp số, Phân tích một số ra thừa số nguyên tố (có đáp án 2024) – Toán 6 Chân trời sáng tạo

Trắc nghiệm Toán lớp 6 Bài 10: Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố

Phần 1. Trắc nghiệm Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố

Dạng 1. Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố

Câu 1. Kết quả của phép tính nào sau đây là số nguyên tố:

A. 15 – 5 + 3

B. 7.2 + 1

C. 14.6:4

D. 6.4 − 12.2

Trả lời:

A.15 – 5 + 3 = 13 là số nguyên tố

B.7.2 + 1 = 14 + 1 = 15, ta thấy 15 có ước 1; 3; 5; 15 nên 15 là hợp số.

C.14.6:4 = 84:4 = 21, ta thấy 21 có ước 1; 3; 7; 21 nên 21 là hợp số

D.6.4 − 12.2 = 24 – 24 = 0, ta thấy 0 không là số nguyên tố, không là hợp số.

Đáp án cần chọn là: A

Câu 2. Thay dấu * để được số nguyên tố $\overline{3*}$ :

A. 7

B. 4

C. 6

D. 9

Trả lời:

Đáp án A: Vì 37chỉ chia hết cho 1 và 37 nên 37 là số nguyên tố, do đó chọn A.

Đáp án B: 34không phải là số nguyên tố (34chia hết cho {2; 4;…}). Do đó loại B.

Đáp án C: 36không phải là số nguyên tố (36 chia hết cho {1; 2; 3;...; 36}). Do đó loại C.

Đáp án D: 39không phải là số nguyên tố (39 chia hết cho {1; 3;...; 39}). Do đó loại D.

Đáp án cần chọn là: A

Câu 3. Khẳng định nào sau đây là đúng:

A. A = {0; 1} là tập hợp số nguyên tố

B. A = {3; 5} là tập hợp số nguyên tố

C. A = {1; 3; 5} là tập hợp các hợp số

D. A = {7; 8} là tập hợp số hợp số

Trả lời:

Đáp án A:Sai vì 0 và 1 không phải là số nguyên tố.

Đáp án C: Sai vì 1 không phải là hợp số, 3,5 là các số nguyên tố.

Đáp án D: Sai vì 7 không phải là hợp số.

Đáp án B: Đúng vì 3;5 đều là số nguyên tố

Đáp án cần chọn là: B

Câu 4. Thay dấu * để được số nguyên tố 

$\overline{*1}$

A. 2

B. 8

C. 5

D. 4

Trả lời:

Dấu * có thể nhận các giá trị {2; 8; 5; 4}

+) Ta có 21 có các ước 1; 3; 7; 21 nên 21 là hợp số. Loại A

+) 81 có các ước 1; 3; 9; 27; 81 nên 81 là hợp số. Loại B

+) 51 có các ước 1; 3; 17; 51 nên 51 là hợp số. Loại C

+) 41 chỉ có hai ước là 1;41 nên 41 là số nguyên tố.

Đáp án cần chọn là: D

Câu 5. Cho các số 21; 77; 71; 101. Chọn câu đúng.

A. Số 21 là hợp số, các số còn lại là số nguyên tố

B. Có hai số nguyên tố và hai hợp số trong các số trên.

C. Chỉ có một số nguyên tốcòn lại là hợp số

D. Không có số nguyên tố nào trong các số trên

Trả lời:

+ Số 21 có các ước 1; 3; 7; 21 nên 21 là hợp số

+ Số 77 có các ước 1; 7; 11; 77 nên 77 là hợp số

+ Số 71 chỉ có hai ước là 1; 71 nên 71 là số nguyên tố.

+ Số 101 chỉ có hai ước là 1; 101 nên 101 là số nguyên tố.

Như vậy có hai số nguyên tố là 71; 101 và hai hợp số là 21; 77.

Đáp án cần chọn là: B

Câu 6. Cho A = 90.17 + 34.40 + 12.51 và B = 5.7.9 + 2.5.6 . Chọn câu đúng.

A. A là số nguyên tố, B là hợp số

B. A là hợp số, B là số nguyên tố

C. Cả A và B là số nguyên tố

D. Cả A và B đều là hợp số

Trả lời:

+) Ta có A = 90.17 + 34.40 + 12.51

Nhận thấy 17⋮17; 34⋮17; 51⋮17nên A = 90.17 + 34.40 + 12.51

chia hết cho 17 nên ngoài ước là 1 và chính nó thì A còn có ước là 17. Do đó A là hợp số.

+) Ta có B = 5.7.9 + 2.5.6 = 5.(7.9 + 2.6)⋮5 nên B = 5.7.9 + 2.5.6

ngoài ước là 1 và chính nó thì A còn có ước là 5. Do đó B là hợp số.

Vậy cả A và B đều là hợp số.

Đáp án cần chọn là: D

Câu 7. Khẳng định nào là sai:

A. 0và 1không là số nguyên tố cũng không phải hợp số.

B. Cho số a > 1, a có 2 ước thì a là hợp số.

C. 2 là số nguyên tố chẵn duy nhất.

D. Số nguyên tố là số tự nhiên lớn hơn 1 mà chỉ có hai ước là 1 và chính nó.

Trả lời:

+) Số a phải là số tự nhiênlớn hơn 1 và có nhiều hơn 2 ước thì aa mới là hợp số nên B sai.

+) 1 là số tự nhiên chỉ có 1 ước là 1 nên không là số nguyên tố và 0 là số tự nhiên nhỏ hơn 1 nên không là số nguyên tố. Lại có 0 và 1 đều không là hợp số do đó A đúng.

+) Số nguyên tố là số tự nhiên lớn hơn 1 mà chỉ có hai ước là 1 và chính nó nên D đúng và suy ra 2 là số nguyên tốchẵn duy nhất nên C đúng.

Đáp án cần chọn là: B

Câu 8. Số nào trong các số sau không là số nguyên tố?

A. 2

B. 3

C. 5

D. 9

Trả lời:

9 chia hết cho 3 nên 3 là một ước của 9. Mà 3 khác 1 và khác 9 nên 9 không là số nguyên tố.

Vậy 9 là số cần tìm.

Đáp án cần chọn là: D

Câu 9. Phân tích số a ra thừa số nguyên tố $a=p_1^{m_1}.p_2^{m_2}\mathrm{...}{p}_k^{m_k}$ . Khẳng định nào sau đây là đúng:

A. Các số $p_1;p_2;\mathrm{...}{p}_k$ là các số dương

B. các số $p_1;p_2;\mathrm{...}{p}_k\in P$ (với P là tập hợp các số nguyên tố)

C. các số $p_1;p_2;\mathrm{...}{p}_k\in N$

D. các số $p_1;p_2;\mathrm{...}{p}_k$ tùy ý

Trả lời:

Khi phân tích một số $a=p_1^{m_1}.p_2^{m_2}\mathrm{...}{p}_k^{m_k}$ ra thừa số nguyên tố thì các số $p_1;p_2;\mathrm{...}{p}_k$ phải là các số nguyên tố.

Đáp án cần chọn là: B

Câu 10. Phân tích số 18thành thừa số nguyên tố:

A. 18 = 18.1

B. 18 = 10 + 8

C. 18 = 2.32

D. 18 = 6 + 6 + 6

Trả lời:

- Đáp án A sai vì 1 không phải là số nguyên tố

- Đáp án B sai vì đây là phép cộng.

- Đáp án C đúng vì 2và 3là 2số nguyên tố và 2.32 = 2.9 = 18

- Đáp án D sai vì đây là phép cộng.

Đáp án cần chọn là: C

Câu 11. Cho số a = 22.7, hãy viết tập hợp tất cả các ước của a:

A. Ư(a) = {4; 7}

B. Ư(a)(a) ={1; 4; 7}

C. Ư(a) ={1; 2; 4; 7; 28}

D. Ư(a) ={1; 2; 4; 7; 14; 28}

Trả lời:

Ta có a = 22.7 = 4.7 = 28

28 = 28.1 = 14.2 = 7.4 = 7.2.2, vậy U(28) = {1; 2; 4; 7; 14; 28}

Đáp án cần chọn là: D

Dạng 2. Các dạng toán về số nguyên tố, hợp số , phân tích một số ra thừa số nguyên tố

Câu 1. Số 40 được phân tích thành các thừa số nguyên tố là:

A. 40 = 4.10

B. 40 = 2.20

C. 40 = 22.5

D. 40 = 23.5

Trả lời:

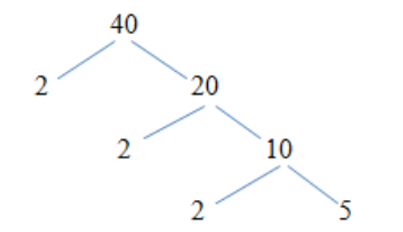
Vậy40 = 2.2.2.5 = 23.5

Đáp án cần chọn là: D

Câu 2. Biết 400 = 24.52. Hãy viết 800 thành tích các thừa số nguyên tố

A. 800 = 22.52

B. 800 = 25.52

C. 800 = 25.55

D. 800 = 400.2

Trả lời:

400 = 24.52

800 = 400.2 = 2.24.52 = 25.52

Đáp án cần chọn là: B

Câu 3. Khi phân tích các số 2150; 1490; 2340 ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố 2; 3 và 5?

A. 2340

B. 2150

C. 1490

D. Cả ba số trên.

Trả lời:

+) Phân tích số 2150 thành thừa số nguyên tố

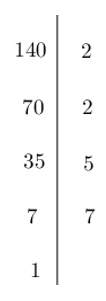
Suy ra 2150 = 2.52.43

+) Phân tích số 1490 thành thừa số nguyên tố

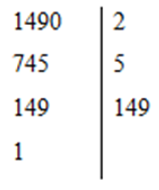
Suy ra 1490 = 2.5.149

+) Phân tích số 2340 thành thừa số nguyên tố

Suy ra 2340 = 22.32.5.13

Vậy có số 2340 thỏa mãn yêu cầu đề bài.

Đáp án cần chọn là: A

Câu 4. 225 chia hết cho tất cả bao nhiêu số nguyên tố?

A. 9

B. 3

C. 5

D. 2

Trả lời:

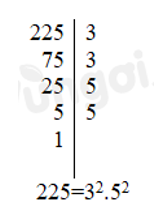
Số 225 chia hết cho các số nguyên tố: 3; 5

Vậy 225 chia hết cho 2 số nguyên tố.

Đáp án cần chọn là: D

Câu 5. Tổng của 3 số nguyên tố là 578. Tìm ra số nguyên tố nhỏ nhất trong 3 số nguyên tố đó.

A. 2

B. 8

C. 5

D. 4

Trả lời:

Tổng 3 số nguyên tố là 578 là số chẵn, nên trong 3 số nguyên tố có ít nhất 1 số là số chẵn. Ta đã biết số 2 là số nguyên tố chẵn duy nhất. Vậy số nguyên tố nhỏ nhất trong 3 số nguyên tố có tổng là 578 là số 2.

Đáp án cần chọn là: A

Câu 6. Chọn khẳng định đúng:

A. Mọi số tự nhiên đều có ước chung với nhau.

B. Mọi số tự nhiên đều có ước là 0.

C. Số nguyên tố chỉ có đúng 1 ước là chính nó.

D. Hai số nguyên tố khác nhau thì không có ước chung.

Trả lời:

A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là 1.

B. Đáp án này sai, vì 0 không là ước của 1 số nào cả.

C. Đáp án này sai, vì số nguyên tố có 2 ước là 1 và chính nó.

D. Đáp án này sai, vì 2 số nguyên tố có ước chung là 1.

Đáp án cần chọn là: A

Câu 7. Số nguyên tố nhỏ hơn 30 là:

A. 23

B. 31

C. 27

D. 32

Trả lời:

Các số nguyên tố nhỏ hơn 30 là:2; 3; 5; 7; 9; 11; 13; 17; 19; 23; 29.

Số cần tìm là 23.

Đáp án cần chọn là: A

Câu 8. Một ước nguyên tố của 91 là

A. 1

B. 2

C. 3

D. 7

Trả lời:

91 có tổng các chữ số bằng 10 không chia hết cho 3 nên 3 không là ước nguyên tố của 91

91 có chữ số tận cùng là 1 nên 91 không chia hết cho 2, do đó 2 không là ước nguyên tố.

Một ước số nguyên tố của 91 là: 7.

Đáp án cần chọn là: D

Câu 9. Cho a2.b.7 = 140 với a, b là các số nguyên tố, vậy a có giá trị là bao nhiêu:

A. 1

B. 2

C. 3

D. 4

Trả lời:

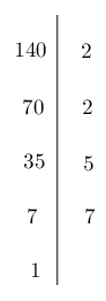
Suy ra

140 = 22.5.7 = a2.b.7 nên a = 2.

Đáp án cần chọn là: B

Câu 10. Cho số 150 = 2.3.52, số lượng ước của 150là bao nhiêu:

A. 6

B. 7

C. 8

D. 12

Trả lời:

Ta có

150 = 2.3.52, vậy x = 1; y = 1; z = 2

Vậy số lượng ước của số 150là (1+1)(1+1)(2+1) = 2.2.3 = 12

Đáp án cần chọn là: D

Câu 11. Có bao nhiêu số nguyên tố x thỏa mãn 50 < x < 60?

A. 2

B. 8

C. 5

D. 4

Trả lời:

Các số x thỏa mãn 50 < x < 60 là 51; 52; 53; 54; 55; 56; 57; 58; 59

Trong đó các số nguyên tố là 53; 59.

Vậy có hai số nguyên tố thỏa mãn đề bài.

Đáp án cần chọn là: A

Câu 12. Tìm tất cả các số tự nhiên nn để n2 + 12n là số nguyên tố.

A. n = 11

B. n = 13

C. n = 2

D. n = 1

Trả lời:

Ta có

n2 + 12n = n(n + 12); n + 12 > 1 nên để n2 + 12n là số nguyên tố thì n = 1.

Thử lại

n2 + 12n = 12 + 12.1 = 13 (nguyên tố)

Vậy với n = 1 thì n2 + 12n là số nguyên tố.

Đáp án cần chọn là: D

Câu 13. Nếu cho 7 hình vuông đơn vị ghép thành hình chữ nhật thì có mấy cách xếp (Không kể việc xoay chiều dài và chiều rộng)?

A. 1

B. 2

C. 3

D. 4

Trả lời:

Nếu xếp 7 hình vuông đơn vị thành hình chữ nhật thì chiều rộng của hình chữ nhật chỉ có thể xếp:

Đáp án cần chọn là: A

Câu 14. Tích của hai số tự nhiên bằng 105. Có bao nhiêu cặp số thỏa mãn?

A. 4

B. 6

C. 10

D. 8

Trả lời:

Gọi hai số tự nhiên cần tìm là a và b(a; b ∈ N)

Ta có a.b = 105

Phân tích số 105 ra thừa số nguyên tố ta được 105 = 3.5.7

Các số a; b là ước của 105 , do đó ta có

a	1	3	5	7	15	21	35	105
b	105	35	21	15	7	5	3	1

Vậy có 8 cặp số thỏa mãn yêu cầu.

Đáp án cần chọn là: D

Câu 15. Số 360 khi phân tích được thành thừa số nguyên tố, hỏi tích đó có bao nhiêu thừa số là số nguyên tố?

A. 3

B. 4

C. 5

D. 6

Trả lời:

Ta có

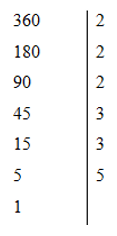
Nên 360 = 23.32.5

Vậy cóthừa số nguyên tố sau khi phân tích là 2; 3 và 5.

Đáp án cần chọn là: A

Câu 16. Số các ước của số 192 là

A. 7

B. 16

C. 14

D. 12

Trả lời:

Ta có

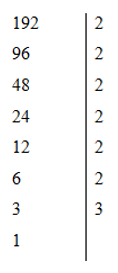
Nên

192=26.3 nên số ước của 192 là

(6+1)(1+1) = 14 ước.

Đáp án cần chọn là: C

Câu 17. Một hình vuông có diện tích là 1936m2. Tính cạnh của hình vuông đó.

A. 44

B. 46

C. 22

D. 48

Trả lời:

Phân tích số 1936 ra thừa số nguyên tố ta được

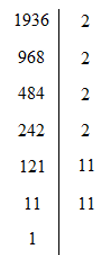
Hay 1936 = 24.112 = (22.11).(22.11) = 44.44

Vậy cạnh hình vuông bằng 44m.

Đáp án cần chọn là: A

Câu 18. Có bao nhiêu số nguyên tố p sao cho p + 4 và p + 8 cũng là số nguyên tố.

A. 2

B. 1

C. 5

D. 4

Trả lời:

Đặt p = 3a + r (r = 0; 1; 2; a∈N)

Với r = 1 ta có p + 8 = 3a + r + 8 = (3a + 9)⋮3, (3a + 9) > 3nên p + 8 là hợp số.

Do đó loại r = 1.

Với r = 2 ta có p + 4 = 3a + r + 4 = (3a + 6)⋮3, (3a + 6) > 3 nên p + 4 là hợp số.

Do đó loại r = 2.

Do đó r = 0; p = 3a là số nguyên tố nên a = 1 ⇒ p = 3.

Ta có p + 4 = 7; p + 8 = 11 là các số nguyên tố.

Vậy p = 3.

Có một số nguyên tố pp thỏa mãn đề bài.

Đáp án cần chọn là: B

Câu 19. Cho nguyên tố p chia cho 42 có số dư r là hợp số. Tìm r.

A. r = 29

B. r = 15

C. r = 27

D. r = 25

Trả lời:

Ta có p = 42.a + r = 2.3.7.a + r (a, r∈N; 0 < r < 42)

Vì p là số nguyên tố nên r không chia hết cho 2; 3; 7.

Các hợp số nhỏ hơn 42 không chia hết cho 2 là 9; 15; 21; 25; 27; 33; 35; 39

Loại bỏ các số chia hết cho 3 và 7 ta còn số 25.

Vậy r = 25.

Đáp án cần chọn là: D

Câu 20. Cho phép tính $\overline{ab}.c=424$ . Khi đó cc bằng bao nhiêu?

A. 9

B. 8

C. 5

D. 6

Trả lời:

Vì $\overline{ab}.c=424$ là ước có hai chữ số của 424.

Phân tích số 424 ra thừa số nguyên tố ta được

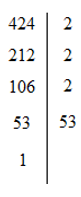
Hay 424=23.53

Các ước của 424 là 1; 2; 4; 8; 53; 106; 212; 424

Suy ra suy ra c = 424:53 = 8.

Đáp án cần chọn là: B

Phần 2. Lý thuyết Số nguyên tố, Hợp số, Phân tích một số ra thừa số nguyên tố

1. Số nguyên tố. Hợp số

− Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

− Hợp số là số tự nhiên lớn hơn 1 có nhiều hơn hai ước.

Ví dụ:

+ Số 13 chỉ có hai ước là 1 và 13 nên 13 là số nguyên tố.

+ Số 15 có bốn ước là 1; 3; 5; 15 nên 15 là hợp số.

Lưu ý: Số 0 và số 1 không là số nguyên tố cũng không là hợp số.

2. Phân tích một số ra thừa số nguyên tố

a. Thế nào là phân tích một số ra thừa số nguyên tố?

Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

Chú ý:

− Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố.

− Mỗi số nguyên tố chỉ có một dạng phân tích ra thừa số nguyên tố là chính số đó.

− Có thể viết gọn dạng phân tích một số ra thừa số nguyên tố bằng cách dùng lũy thừa.

Ví dụ:

- Số 5 là số nguyên tố và dạng phân tích ra thừa số nguyên tố của nó là 5.

- Số 18 là hợp số và 18 được phân tích ra thừa số nguyên tố là:

18 = 2 . 3 . 3 (hoặc viết gọn là 18 = 2 . 32).

b. Cách phân tích một số ra thừa số nguyên tố

Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc.

Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.

Ví dụ: Số 76 được phân tích ra thừa số nguyên tố theo cột dọc như sau:

76	2
38	2
19	19
1

Vậy 76 = 22 . 19.

Chú ý: Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.

Cách 2: Phân tích một số ra thừa số nguyên tố theo sơ đồ cây.

Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.

Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.

Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.

Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.

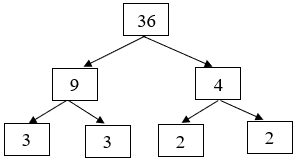
Ví dụ: Số 36 được phân tích ra thừa số nguyên tố theo sơ đồ cây như sau:

Vậy 36 = 32 . 22.