30 câu Trắc nghiệm Tập hợp, Phần tử của tập hợp (có đáp án 2024) – Toán 6 Chân trời sáng tạo

Trắc nghiệm Toán lớp 6 Bài 1: Tập hợp, Phần tử của tập hợp

Phần 1. Trắc nghiệm Tập hợp, Phần tử của tập hợp

Dạng 1.Tập hợp. Phần tử của tập hợp

Câu 1. Dùng ba chữ số 0; 4; 6 để viết tập hợp các số có ba chữ số khác nhau. Hỏi tập này có bao nhiêu phần tử?

A. 3

B. 4

C. 2

D. 5

Trả lời:

Với ba chữ số 0; 4; 6 ta có thể lập được bốn số có ba chữ số khác nhaulà 640; 604; 406; 460 . Do đó tập hợp cần tìm có bốn phần tử.

Đáp án cần chọn là: B

Câu 2. Cho tập hợp E = {0; 2; 4; 6; 8}. Hãy chỉ ra tính chất đặc trưng cho các phần tử của tập hợp E.

A. Các số tự nhiên chẵn nhỏ hơn 10

B. Các số tự nhiên chẵn nhỏ hơn 11

C. Các số tự nhiên chẵn nhỏ hơn 12

D. Các số tự nhiên chẵn nhỏ hơn 8

Trả lời:

Các phần tử của tập hợp E đều là các số tự nhiên chẵn nhỏ hơn 10

Tính chất đặc trưng của các phần tử trong E là “các số tự nhiên chẵn nhỏ hơn 10”

Đáp án cần chọn là: A

Câu 3. Cho tập hợp A = {x∈N|2 < x ≤ 7} . Kết luận nào sau đây không đúng?

A. 7∈A

B. Tập hợp A có 5 phần tử

C. 2∈A

D. Tập hợp A gồm các số tự nhiên lớn hơn 2 và nhỏ hơn hoặc bằng 7

Trả lời:

Trong cách viết A = {x∈N|2 < x ≤ 7}, ta chỉ ra tính chất đặc trưng cho các phần tử xx của tập hợp A đó là x > 2 và x ≤ 7 . Do đó 2 không là phần tử của tập A.

Đáp án cần chọn là: C

Câu 4. Cho tập hợp A = {x∈N|1990 ≤ x ≤ 2009}. Số phần tử của tập hợp A là

A. 20

B. 21

C. 19

D. 22

Trả lời:

Các số tự nhiên liên tiếp hơn kém nhau 1 đơn vị. Vì vậy số phần tử của tập hợp A là:

2009 – 1990 + 1 = 20.

Đáp án cần chọn là: A

Câu 5. Tập hợp C các số tự nhiên x sao cho x – 10 = 15 có số phần tử là

A. 4

B. 2

C. 1

D. 3

Trả lời:

Ta có:

x – 10 = 15

x = 15 + 10

x = 25

nên C = {25} do đó CC có một phần tử.

Đáp án cần chọn là: C

Câu 6. Cách viết tập hợp nào sau đây là đúng?

A. A = [0; 1; 2; 3]

B. A = (0; 1; 2; 3)

C. A = 1; 2; 3

D. A = {0; 1; 2; 3}

Trả lời:

Cách viết đúng là A = {0; 1; 2; 3}.

Đáp án cần chọn là: D

Câu 7. Cho B = {2; 3; 4; 5}. Chọn câu sai.

A. 2∈B

B. 5∈B

C. 1∉B

D. 6∈B

Trả lời:

2 và 5 là các phần tử của B nên A, B đúng.

1 không là phần tử của B nên C đúng.

Ta thấy 6 không là phần tử của tập hợp B nên 6∉B. Do đó D sai.

Đáp án cần chọn là: D

Câu 8. Cho A là tập hợp các số chẵn lớn hơn 15. Số nào trong các số sau là một phần tử của A?

A. 0

B. 13

C. 20

D. 21

Trả lời:

Số 0 và 13 là các số nhỏ hơn 15 nên 0 và 13 không là phần tử của A => Đáp án A, B sai

Số 21 là số lẻ nên 21 không là phần tử của A => Đáp án D sai

Số 20 là số lớn hơn 15 và là số chẵn nên 20 là một phần tử của A => Đáp án C đúng.

Đáp án cần chọn là: C

Câu 9. Hệ Mặt Trời gồm có Mặt Trời ở trung tâm và 8 thiên thể quanh quanh Mặt Trời gọi là các hành tinh. Đó là sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương.

Cho S là tập hợp các hành tinh của Hệ Mặt Trời. Khẳng định nào sau đây đúng?

A. S là tập hợp có 8 phần tử.

B. Sao Thủy không thuộc S.

C. S là tập hợp có 9 phần tử.

D. Mặt Trời là một phần tử của S.

Trả lời:

Thổ, Sao Thiên Vương, Sao Hải Vương

Hệ Mặt Trời có 8 hành tinh nên S có 8 phần tử => A đúng, C sai

Sao Thủy là một hành tinh của Hệ Mặt Trời => B sai.

Mặt Trời không là hành tinh nên Mặt Trời không là một phần tử của S => D sai

Đáp án cần chọn là: A

Câu 10. A là tập hợp tên các hình trong Hình 3:

Khẳng định nào sau đây đúng?

A. A = {Hình chữ nhật, hình vuông, hình tam giác}

B. A = {Hình chữ nhật, hình vuông, hình tam giác, hình bình hành}

C. A = {Hình chữ nhật, hình vuông, hình tam giác, hình bình hành, hình thang cân}

D. A = {Hình chữ nhật, hình vuông, hình tam giác, hình bình hành, hình thang}

Trả lời:

Các hình trên theo thứ tự từ trái sang phải lần lượt là hình chữ nhật, hình vuông, hình bình hành, hình tam giác, hình thang.

Vậy A = {hình chữ nhật, hình vuông, hình bình hành, hình tam giác, hình thang}

Đáp án cần chọn là: D

Dạng 2.Các dạng toán về tập hợp, phần tử của tập hợp

Câu 1. Viết tập hợp A = {16; 17; 18; 19} dưới dạng chỉ ra tính chất đặc trưng.

A. A = {x∈N|15 < x < 19}

B. A = {x∈N|15 < x < 20}

C. A = {x∈N|16 < x < 20}

D. A = {x∈N|15 < x ≤ 20}

Trả lời:

Nhận thấy các số 16; 17; 18; 19 là các số tự nhiên lớn hơn 15 và nhỏ hơn 20

Nên A = {x∈N|15 < x < 20}.

Đáp án cần chọn là: B

Câu 2. Viết tập hợp A các số tự nhiên lớn hơn 5 và nhỏ hơn 10.

A. A = {6; 7; 8; 9}.

B. A = {5; 6; 7; 8; 9}.

C. A = {6; 7; 8; 9; 10}.

D. A = {6; 7; 8}.

Trả lời:

Tập hợp A các số tự nhiên lớn hơn 5 và nhỏ hơn 10 là A = {6; 7; 8; 9}.

Đáp án cần chọn là: A

Câu 3. Viết tập hợp P các chữ cái khác nhau trong cụm từ: “ HOC SINH”

A. P = {H; O; C; S; I; N; H}.

B. P = {H; O; C; S; I; N}.

C. P = {H; C; S; I; N}.

D. P = {H; O; C; H; I; N}.

Trả lời:

Các chữ cái khác nhau trong cụm từ “ HOC SINH” là H; O; C; S; I; N

Nên P = {H; O; C; S; I; N}.

Đáp án cần chọn là: B

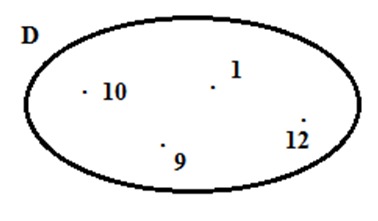
Câu 4. Cho hình vẽ.

Tập hợp D là

A. D = {8; 9; 10; 12}

B. D = {1; 9; 10}

C. D = {9; 10; 12}

D. D = {1; 9; 10; 12}

Trả lời:

Ta có các số trong vòng tròn là 1, 9, 10, 12 nên tập hợp D = {1; 9; 10; 12}.

Đáp án cần chọn là: D

Câu 5. Cho B là tập hợp các số tự nhiên nhỏ hơn 10. Trong các khẳng định sau, có bao nhiêu khẳng định sai?

1. 2∈B

2. 5∉B

3. B = {0;1;2;3;4;5;6;7;8;9;10}

4. B={9;8;7;6;5;4;3;2;1;0}

5. B={0;1;1;2;3;4;5;6;7;8;9}

A. 1

B. 2

C. 3

D. 4

Trả lời:

Số 2 là số tự nhiên nhỏ hơn 10 nên 2∈B =>Khẳng định 1 đúng.

Số 5 là số tự nhiên nhỏ hơn 10 nên 5∈B =>Khẳng định 2 sai.

Tập hợp B là tập hợp các số tự nhiên nhỏ hơn 10 nên các phần tử của B là:

1; 2; 3; 4; 5; 6; 7; 8; 9

⇒ B = {1; 2; 3; 4; 5; 6; 7; 8; 9} = {9; 8; 7; 6; 5; 4; 3; 2; 1}

=>Khẳng định 4 đúng.

Tập hợp B trong khẳng định 3 có chứa số 10 mà 10 không thuộc B

=>Khẳng định 3 sai.

B = {1; 1; 2; 3; 4; 5; 6; 7; 8; 9} có số 1 được liệt kê hai lần

=> Khẳng định 5 sai

Vậy có 3 khẳng định sai.

Đáp án cần chọn là: C

Câu 6. Viết tập hợpA = {x|22 < x ≤ 27} dưới dạng liệt kê các phần tử ta được:

A. A = {22; 23; 24; 25; 26}

B. A = {22; 23; 24; 25; 26; 27}

C. A = {23; 24; 25; 26; 27}

D. A = {23; 24; 25; 26}

Trả lời:

Các số lớn hơn 22 và nhỏ hơn hoặc bằng 27 là 23; 24; 25; 26; 27.

Nên A = {23; 24; 25; 26; 27}.

Đáp án cần chọn là: C

Câu 7. Tập hợp P gồm các số tự nhiên lớn hơn 50 và không lớn hơn 57. Kết luận nào sau đây là sai?

A. 55∈P

B. 57∈P

C. 50∉P

D. 58∈P

Trả lời:

Các số tự nhiên lớn hơn 50 và không lớn hơn 57 là 51; 52; 53; 54; 55; 56; 57

Nên P = {51; 52; 53; 54; 55; 56; 57}

Do đó 58∉P nên D sai.

Đáp án cần chọn là: D

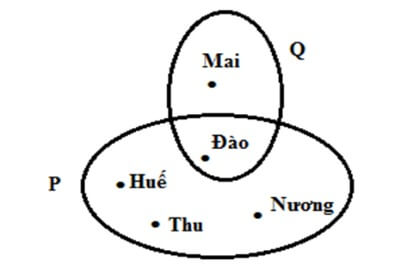
Câu 8. Cho hình vẽ sau:

Viết tập hợp P và Q.

A. P ={ Huế; Thu; Nương}; Q = {Đào; Mai}

B. P = {Huế; Thu; Nương; Đào}; Q = {Đào; Mai}

C. P = {Huế; Thu; Nương; Đào}; Q = {Mai}

D. P = {Huế; Thu; Đào}; Q = {Đào; Mai}

Trả lời:

Ta có P = {Huế; Thu; Nương; Đào}

Q = {Đào; Mai}

Đáp án cần chọn là: B

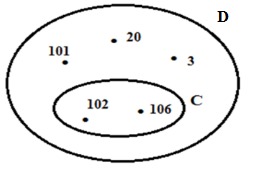
Câu 9. Cho hình vẽ sau:

Viết tập hợp C và D.

A. C = {102; 106} và D = {20; 101; 102; 106}

B. C = {102; 106} và D = {3; 20; 102; 106}

C. C = {102; 106} và D = {3; 20; 101}

D. C = {102; 106} và D = {3; 20; 101; 102; 106}

Trả lời:

C = {102; 106} và D = {3; 20; 101; 102; 106}

Đáp án cần chọn là: D

Câu 10. Số phần tử của tập hợp các số tự nhiên lẻ lớn hơn 1010 nhỏ hơn 5050 là

A. 16

B. 20

C. 18

D. 19

Trả lời:

Các số tự nhiên lẻ lớn hơn 10 và nhỏ hơn 50 là 11; 13; 15;...; 47; 49.

Nên có (49 − 11):2 + 1 = 20 số tự nhiên lẻ lớn hơn 10 và nhỏ hơn 50.

Vậy số phần tử của tập hợp các số tự nhiên lẻ lớn hơn 10 nhỏ hơn 50 là 20.

Đáp án cần chọn là: B

Câu 11. Số phần tử của tập hợp P gồm các chữ cái trong cụm từ “ WORLD CUP” là

A. 9

B. 6

C. 8

D. 7

Trả lời:

Các chữ cái trong cụm từ“ WORLD CUP” là W; O; R; L; D; C; U; P.

Nên tập hợp P = {W; O; R; L; D; C; U; P} bao gồm 88 phần tử.

Đáp án cần chọn là: C

Phần 2. Lý thuyết Tập hợp, Phần tử của tập hợp

1. Tập hợp, phần tử

Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.

Mối quan hệ giữa tập hợp và phần tử: Tập hợp chứa phần tử (nếu có) và phần tử nằm trong tập hợp.

Tập hợp là khái niệm cơ bản thường dùng trong toán học và cuộc sống. Ta hiểu tập hợp thông qua các ví dụ.

Ví dụ:

a) Tập hợp các bạn nữ trong lớp 6A bao gồm tất cả các bạn nữ của lớp 6A.

Đối tượng của tập hợp này là các bạn nữ của lớp 6A. Mỗi một bạn là một phần tử.

b) Tập hợp các số nhỏ hơn gồm tất cả các số nhỏ hơn 6, đó là 0; 1; 2; 3; 4; 5.

Mỗi một số trong 6 số này là một phần tử của tập hợp, chẳng hạn số 0 là một phần tử, số 1 cũng là một phần tử.

2. Các kí hiệu tập hợp

- Người ta thường đặt tên cho tập hợp bằng các chữ cái in hoa: A, B, C, D, ... và sử dụng các chữ cái thường a, b, c, ... để kí hiệu cho phần tử.

- Các phần tử của tập hợp được viết trong dấu ngoặc nhọn { }, cách nhau bởi dấu chấm phẩy dấu “;”. Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.

- Phần tử x thuộc tập hợp A được kí hiệu là x $\in$ A, đọc là “x thuộc A”. Phần tử y không thuộc tập hợp A được kí hiệu là y $\notin$ A, đọc là “y không thuộc A”.

Ví dụ: Tập hợp M gồm tất cả các số nhỏ hơn 5

Kí hiệu: M = {0; 1; 2; 3; 4} = {2; 1; 0; 3; 4}.

Mỗi số 0; 1; 2; 3; 4 đều là một phần tử của tập hợp M.

Số 6 không là phần tử của M (8 không thuộc M).

Ta viết: 0 ∈ M; 1 ∈ M; 2 ∈ M; 3 ∈ M; 4 ∈ M và 8 ∉ M.

3. Các cách cho một tập hợp

Nhận xét. Để cho một tập hợp, thường có hai cách:

• Liệt kê các phần tử của tập hợp.

• Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

Ngoài 2 cách cho tập hợp như trên, người ta còn minh họa bằng hình vẽ (Sơ đồ Venn).

Ví dụ: Tập hợp A gồm tất cả các số tự nhiên nhỏ hơn 6.

- Liệt kê: A = {0; 1; 2; 3; 4; 5}.

- Chỉ ra tính chất đặc trưng: B = {x | x < 6}.

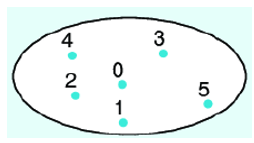
- Sơ đồ Venn:

4. Tập rỗng

Tập rỗng là tập hợp không có phần tử nào, kí hiệu $\varnothing$.

Ví dụ: Giả sử các học sinh lớp 6A không có bạn nào trên 55kg. Nên tập hợp các bạn trên 55kg của lớp 6A là tập rỗng.