30 câu Trắc nghiệm Phép cộng và phép trừ phân số (có đáp án 2024) – Toán 6 Chân trời sáng tạo
Bộ 30 câu hỏi trắc nghiệm Toán 6 (có đáp án) Bài 4: Phép cộng và phép trừ phân số đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 6 Bài 4.
Nội dung bài viết
Xem thêm »
Trắc nghiệm Toán lớp 6 Bài 4: Phép cộng và phép trừ phân số
Phần 1. Trắc nghiệm Phép cộng và phép trừ phân số
Dạng 1. Phép cộng và phép trừ phân số
Câu 1: Cho ba vòi nước cùng chảy vào một bể cạn. Vòi Achảy một mình thì sau 6 giờ sẽ đầy bể, vòi Bchảy một mình thì mất 3 giờ đầy bể, vòi Cthì mất 2 giờ đầy bể. Hỏi nếu cả ba vòi cùng chảy một lúc thì trong bao lâu sẽ đầy bể?
A.4 giờ
B.3 giờ
C.1 giờ
D.2 giờ
Trả lời:
Một giờ vòi A chảy được là: 1:6=16 (bể)
Một giờ vòi B chảy được là: 1:3=13 (bể)
Một giờ vòi C chảy được là:1:2=12 (bể)
Một giờ cả ba vòi chảy được là: 16+13+12=66=1 (bể)
Vậy trong 1 giờ cả ba vòi chảy được đầy bể.
Đáp án cần chọn là: C
Câu 2: Tìm x biết x−15=2+−34
A.x=2120
B.x=2920
C.x=−310
D.x=−910
Trả lời:
x−15=2+−34
x−15=54
x=54+15
x=2920
Đáp án cần chọn là: B
Câu 3: Tìm x ∈ Zbiết 56+−78≤x24≤−512+58 .
A. x ∈ {0; 1; 2; 3; 4}
B. x ∈ {−1; 0; 1; 2; 3; 4; 5}
C. x ∈ {−1; 0; 1; 2; 3; 4}
D. x ∈ {0; 1; 2; 3; 4; 5}
Trả lời:
56+−78≤x24≤−512+58−124≤x24≤524−1≤x≤5x∈{−1;0;1;2;3;4;5}
Đáp án cần chọn là: B
Câu 4: Số đối của phân số 137 là:
A. −137
B. 13−7
C. −137
D.Tất cả các đáp án trên đều đúng
Trả lời:
Số đối của phân số 137 là −137 hoặc −137 hoặc13−7
Đáp án cần chọn là: D
Câu 5: Cặp phân số nào sau đây là hai số đối nhau?
A.−23;32
B.−1213;13−12
C.12;−12
D.34;−43
Trả lời:
Đáp án A: Số đối của −23 là 23 chứ không phải 32 nên A sai.
Đáp án B: Số đối của −1213 là 1213 chứ không phải 13−12 nên B sai.
Đáp án C: Số đối của 12 là −12 nên C đúng.
Đáp án D: Số đối của 34 là −34 hoặc 3−4hoặc −34 chứ không phải −43 nên D sai.
Đáp án cần chọn là: C
Câu 6: Chọn câu đúng. Với a; b; m ∈ Z; m ≠ 0ta có
A.am+bm=a−bm
B.am+bm=a.bm
C.am+bm=a+bm
D.am+bm=a+bm+m
Trả lời:
Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu.
am+bm=a+bm
Đáp án cần chọn là: C
Câu 7: Phép cộng phân số có tính chất nào dưới đây?
A.Tính chất giao hoán
B.Tính chất kết hợp
C.Tính chất cộng với 0
D.Cả A, B, C đều đúng
Trả lời:
Phép cộng phân số có các tính chất:
+) Tính chất giao hoán: khi đổi chỗ các phân số trong một tổng thì tổng không đổi.
+) Tính chất kết hợp: Muốn cộng một tổng hai phân số với phân số thứ ba, ta có thể cộng phân số thứ nhất với tổng hai phân số còn lại.
+) Tính chất cộng với 0: tổng của một phân số với 0 bằng chính phân số đó.
Đáp án cần chọn là: D
Câu 8: Tổng 46+2781 có kết quả là
A.13
B.43
C.34
D. 1
Trả lời:
46+2781=23+13=33=1
Đáp án cần chọn là: D
Câu 9: Tính tổng hai phân số 3536 và−12536
A.−52
B.−295
C.−409
D.409
Trả lời:
3536+−12536=35+(−125)36=−9036=−52
Đáp án cần chọn là: A
Câu 10: Chọn câu sai
A.32+23>1
B.32+23=136
C.34+(−417)=3568
D.412+2136=1
Trả lời:
Đáp án A: 32+23=96+46=136>1 nên A đúng
Đáp án B: 32+23=96+46=136 nên B đúng.
Đáp án C:34+(−417)=5168+−1668=3568 nên C đúng.
Đáp án D:412+2136=412+712=1112<1nên D sai.
Đáp án cần chọn là: D
Câu 11: Số đối của −(−227) là
A.272
B. −(−227)
C. 227
D. −227
Trả lời:
Ta có: −(−227)=227 nên số đối của 227là−227
Đáp án cần chọn là: D
Câu 12: Tính−16−−49
A.518
B.536
C.−1118
D.−1336
Trả lời:
−16−−49=−16+49=−318+818=518
Đáp án cần chọn là: A
Câu 13: Tìm x biếtx+114=57
A.914
B.114
C.1114
D.12
Trả lời:
x+114=57x=57−114x=914
Đáp án cần chọn là: A
Câu 14: Điền số thích hợp vào chỗ chấm 13+...24=38
A.2
B.1
C.−1
D.5
Trả lời:
Đặt số cần điền vào chỗ chấm là x ta có:
13+x24=38x24=38−13x24=124x=1
Vậy số cần điền vào chỗ trống là 1
Đáp án cần chọn là: B
Câu 15: Chọn câu đúng
A.413−12=526
B.12−13=56
C.1720−15=1320
D.515−13=15
Trả lời:
Đáp án A: 413−12=826−1326=−526≠526 nên A sai.
Đáp án B: 12−13=36−26=16≠56 nên B sai.
Đáp án C: 1720−15=1720−420=1320 nên C đúng.
Đáp án D: nên D sai.
Đáp án cần chọn là: C
Câu 16: Phép tính 97−512 là
A.7384
B.−1384
C.8384
D.14384
Trả lời:
Ta có:
97−512=97+(−512)=10884+(−3584)=108+(−35)84=7384
Đáp án cần chọn là: A
Dạng 2. Các dạng toán về phép cộng và phép trừ phân số
Câu 1: Cho M=(2131+−167)+(4453+1031)+953 và
N=12+−15+−57+16+−335+13+141.
Chọn câu đúng.
A.M=27;N=141
B.M=0;N=141
C.M=−167;N=8341
D.M=−27;N=141
Trả lời:
M=(2131+−167)+(4453+1031)+953M=2131+−167+4453+1031+953M=(2131+1031)+(4453+953)+−167M=1+1+−167M=2+−167M=−27
N=12+−15+−57+16+−335+13+141N=(12+16+13)+(−15+−57+−335)+141N=3+1+26+(−7)+(−25)+(−3)35+141N=1+(−1)+141N=141
Đáp án cần chọn là: D
Câu 2: Tìm x∈Ζ biết56+−78≤x24≤−512+58
A.x∈{0;1;2;3;4}
B.x∈{−1;0;1;2;3;4;5}
C.x∈{−1;0;1;2;3;4}
D.x∈{0;1;2;3;4;5}
Trả lời:
56+−78≤x24≤−512+58−124≤x24≤524−1≤x≤5x∈{−1;0;1;2;3;4;5}
Đáp án cần chọn là: B
Câu 3: Tìm tập hợp các số nguyên n để n−8n+1+n+3n+1 là một số nguyên
A.n∈{1;−1;7;−7}
B.n∈{0;6}
C.n∈{0;−2;6;−8}
D.n∈{−2;6;−8}
Trả lời:
Ta có:
n−8n+1+n+3n+1=n−8+n+3n+1=2n−5n+1=(2n+2)−7n+1=2(n+1)−7n+1=2(n+1)n+1−7n+1=2−7n+1
Yêu cầu bài toán thỏa mãn nếu 7n+1∈Z hayn + 1 ∈ Ư(7) = {±1; ±7}
Ta có bảng:
| n+1 | 1 | -1 | 7 | -7 |
| n | 0 | -2 | 6 | -8 |
Vậy n ∈ {0; −2; 6; −8}
Đáp án cần chọn là: C
Câu 4: Có bao nhiêu số nguyên x thỏa mãn1541+−13841≤x<12+13+16
A.6
B.3
C.5
D.4
Trả lời:
1541+−13841≤x<12+13+16
−3 ≤ x < 1
x ∈ {− 3; −2; −1;0}
Vậy có tất cả 4 giá trị của x
Đáp án cần chọn là: D
Câu 5: Tính tổng A=12+16+112+…+199.100 ta được
A.S>35
B.S<45
C.S>45
D.Cả A, C đều đúng
Trả lời:
A=12+16+112+…+199.100
A=11.2+12.3+13.4+...+199.100
A=1−12+12−13+13−14+...+199−1100
A=1−1100=99100
So sánh A với 35 và45
Ta có: 35=60100;45=80100
⇒60100<80100<99100⇒A>45>35
Đáp án cần chọn là: D
Câu 6: Thực hiện phép tính 6591+−4455 ta được kết quả là:
A.−5335
B.5135
C.−335
D.335
Trả lời:
6591+−4455=57+−45=2535+−2835=−335
Đáp án cần chọn là: C
Câu 7: Chọn câu đúng
A.−411+7−11>1
B.−411+7−11<0
C.811+7−11>1
D.−411+−711>−1
Trả lời:
Đáp án A: −411+7−11=−411+−711=−1111=−1<1 nên A sai
Đáp án B: −411+7−11=−411+−711=−1111=−1<0 nên B đúng.
Đáp án C: 811+7−11=811+−711=111<1nên C sai.
Đáp án D: −411+−711=−1111=−1 nên D sai.
Đáp án cần chọn là: B
Câu 8: Tìm x biếtx=313+920
A.1233
B.177260
C.187260
D.17726
Trả lời:
313+920=60260+117260=177260
Vậy x=177260
Đáp án cần chọn là: B
Câu 9: Tính hợp lý biểu thức −97+134+−15+−57+34ta được kết quả là
A.=(−97+−57)+(134+34)+−1595
B.115
C.−115
D. −15
Trả lời:
−97+134+−15+−57+34
=(−97+−57)+(134+34)+−15
=−147+164+−15
=(−2)+4+−15
=2+−15
=105+−15
=95
Đáp án cần chọn là: A
Câu 10: ChoA=(14+−513)+(211+−813+34). Chọn câu đúng.
A. A > 1
B.A=211
C. A = 1
D. A = 0
Trả lời:
A=(14+−513)+(211+−813+34)
A=14+−513+211+−813+34
A=(14+34)+(−513+−813)+211
A=1+(−1)+211
A=211
Đáp án cần chọn là: B
Câu 11: Cho S=121+122+123+...+135 . Chọn câu đúng.
A.S>12
B. S < 0
C. S = 2
D. S=12
Trả lời:
S=121+122+123+...+135S=(121+...+125)+(126+...+130)+(131+...+135)S>(125+...+125)+(130+...+130)+(135+...+135)S>15+16+17=107210>12
Vậy S>12
Đáp án cần chọn là: A
Câu 12: Có bao nhiêu cặp số a; b ∈ Z thỏa mãna5+110=−1b
A.0
B.Không tồn tại (a; b)
C.4
D.10
Trả lời:
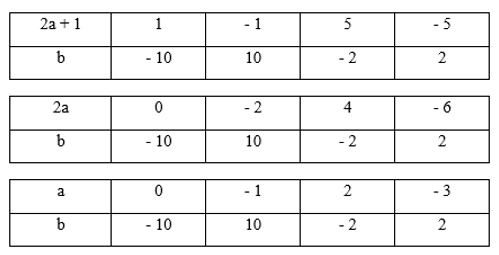
a5+110=−1b2a10+110=−1b2a+110=−1b(2a+1).b=−10
2a + 1 là số lẻ; 2a + 1 là ước của −10
Vậy có 44 cặp số (a;b)(a;b) thỏa mãn bài toán.
Đáp án cần chọn là: C
Câu 13: Kết quả của phép tính 34−720 là:
A.110
B.45
C.25
D.−110
Trả lời:
34−720=1520−720=820=25
Đáp án cần chọn là: C
Câu 14: Giá trị của x thỏa mãn1520−x=716
A. −516
B. 516
C. 1916
D.−1916
Trả lời:
1520−x=716
−x=716−1520−x=−516x=516
Đáp án cần chọn là: B
Câu 15: Tính 415−265−439 ta được
A.139
B.215
C.−265
D.115
Trả lời:
415−265−439=52195−6195−20195=52−6−20195=26195=215
Đáp án cần chọn là: B
Câu 16: Tính hợp lý B=3123−(730+823) ta được
A.2330
B.730
C.−730
D.−2330
Trả lời:
B=3123−(730+823)B=3123−730−823B=(3123−823)−730B=1−730B=2330
Đáp án cần chọn là: A
Câu 17: Cho M=(13+1267+1341)−(7967−2841) và N=3845−(845−1751−311) . Chọn câu đúng.
A. M = N
B. N < 1 < M
C. 1 < M < N
D. M < 1 < N
Trả lời:
M=(13+1267+1341)−(7967−2841)
M=13+1267+1341−7967+2841M=13+(1267−7967)+(1341+2841)M=13+(−1)+1=13
N=3845−(845−1751−311)N=3845−845+1751+311N=(3845−845)+1751+311N=23+13+311N=1+311N=1411
Vìnên M < 1 < N
Đáp án cần chọn là: D
Câu 18: Tìm x sao chox−−712=1718−19
A.−14
B.1712
C.14
D.−1712
Trả lời:
x−−712=1718−19x−−712=56x=56+−712x=14
Đáp án cần chọn là: C
Câu 19: Giá trị nào của x dưới đây thỏa mãn 2930−(1323+x)=769 ?
A.310
B.1323
C.25
D.−310
Trả lời:
2930−(1323+x)=7691323+x=2930−7691323+x=199230x=199230−1323x=310
Đáp án cần chọn là: A
Câu 20: Có bao nhiêu số nguyên xx thỏa mãn −514−3714≤x≤3173−313131737373 ?
A.3
B.5
C.4
D.1
Trả lời:
−514−3714≤x≤3173−313131737373−514+−3714≤x≤3173−313131:10101737373:10101−4214≤x≤3173−3173−3≤x≤0x∈{−3;−2;−1;0}
Vậy có 4 giá trị của x thỏa mãn bài toán.
Đáp án cần chọn là: C
Câu 21: Hai vòi nước cùng chảy vào một bể cạn. Vòi thứ nhất chảy riêng trong 10 giờ đầy bể, vòi thứ hai chảy riêng trong 8 giờ đầy bể. Vòi thứ ba tháo nước ra sau 5 giờ thì bể cạn. Nếu bể đang cạn, ta mở cả ba vòi thì sau 1 giờ chảy được bao nhiêu phần bể?
A.1740
B.140
C.113
D. 1
Trả lời:
Trong 1 giờ, vòi thứ nhất chảy được là:1:10=110(bể)
Trong 1 giờ, vòi thứ hai chảy được là: 1:8=18 (bể)
Trong 1 giờ, vòi thứ ba tháo được là:1:5=15(bể)
Sau 11 giờ, lượng nước trong bể có là:
110+18−15=140 (bể)
Đáp án cần chọn là: B
Câu 22: Cho x là số thỏa mãn x+45.9+49.13+413.17+...+441.45=−3745 . Chọn kết luận đúng:
A.x nguyên âm
B.x = 0
C.x nguyên dương
D.x là phân số dương
Trả lời:
x+45.9+49.13+413.17+...+441.45=−3745x+15−19+19−113+...+141−145=−3745x+15−145=−3745x+845=−3745x=−3745−845x=−1
Vì -1 là số nguyên âm nên đáp án A đúng.
Đáp án cần chọn là: A
Câu 23: Cho P=122+132+...+120022+120032. Chọn câu đúng
A. P > 1
B. P > 2
C. P < 1
D. P < 0
Trả lời:
P=122+132+...+120022+120032<11.2+12.3+...+12001.2002+12002.2003=11−12+12−13+...+12001−12002+12002−12003=1−12003=20022003<1
Vậy P < 1
Đáp án cần chọn là: C
Phần 2. Lý thuyết Phép cộng và phép trừ phân số
1. Phép cộng hai phân số
Quy tắc cộng hai hai phân số cùng mẫu: Muốn cộng hai phân số có cùng mẫu số, ta cộng tử số với nhau và giữ nguyên mẫu số.
Ví dụ 1. Tính: 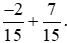 .
.
Lời giải:
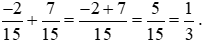
Quy tắc cộng hai phân số khác mẫu: Muốn cộng hai phân số khác mẫu, ta quy đồng mẫu số của chúng
Ví dụ 2. Tính: 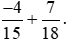 .
.
Lời giải:
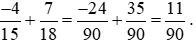
2. Một số tính chất của phép cộng phân số
Phép cộng phân số có các tính chất giao hoán và kết hợp, cộng một phân số với 0 ta được chính nó.
Ví dụ 3. Tính biểu thức sau theo cách hợp lí: 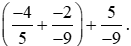 .
.
Lời giải:
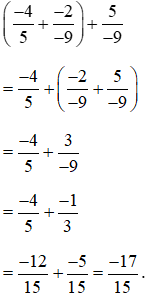
3. Số đối
Hai phân số là đối nhau nếu tổng của chúng bằng 0.
Kí hiệu số đối của phân số 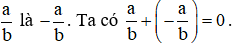 .
.
Mà 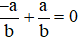 nên ta có:
nên ta có: 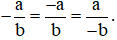 .
.
Ví dụ 4. Tìm số đối của mỗi phân số sau (có dùng kí hiệu số đối của phân số).
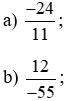
Lời giải:
a) Số đối của phân số 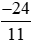 là phân số
là phân số 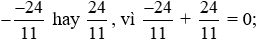
b) Số đối của phân số 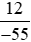 là phân số
là phân số 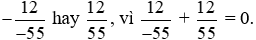 .
.
4. Phép trừ hai phân số
Muốn trừ một phân số cho một phân số, ta lấy phân số thứ nhất cộng với số đối của phân số thứ hai.
Ví dụ 5. Thực hiện phép tính: 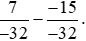 .
.
Lời giải:
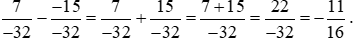
Quy tắc dấu ngoặc:
- Khi bỏ ngoặc có dấu cộng (+) đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc.
- Khi bỏ ngoặc có dấu trừ (−) đằng trước, ta phải đổi dấu tất cả các số hạng trong ngoặc.
Ví dụ 6.
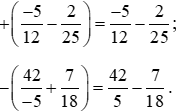
Chú ý: Ta thực hiện được phép cộng và phép trừ phân số với số nguyên bằng cách viết số nguyên ở dạng phân số.
Ví dụ 7. Tính 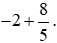 .
.
Lời giải: