30 câu Trắc nghiệm So sánh phân số (có đáp án 2024) – Toán 6 Chân trời sáng tạo

Trắc nghiệm Toán lớp 6 Bài 3: So sánh phân số

Phần 1. Trắc nghiệm So sánh phân số

Câu 1: Không quy đồng mẫu số, em hãy so sánh $\frac{34}{111}$ và $\frac{198}{54}$ :

A.  $\frac{34}{111}<\frac{198}{54}$

B.  $\frac{34}{111}>\frac{198}{54}$

C.  $\frac{34}{111}\ge \frac{198}{54}$

D.  $\frac{34}{111}=\frac{198}{54}$

Trả lời:

Ta có:  $\frac{34}{111}<1$

Và  $\frac{198}{54}>1$

Do vậy:  $\frac{34}{111}<\frac{198}{54}$

Đáp án cần chọn là: A

Câu 2: Chọn câu đúng:

A.  $\frac{11}{12}<\frac{-22}{12}$

B.  $\frac{8}{3}<\frac{-9}{3}$

C.  $\frac{7}{8}<\frac{9}{8}$

D.  $\frac{6}{5}<\frac{4}{5}$

Trả lời:

11 > (−22)  nên $\frac{11}{12}>\frac{-22}{12}$

8 > (−9) nên $\frac{8}{3}>\frac{-9}{3}$

7 < 9  nên $\frac{7}{8}<\frac{9}{8}$

6 > 4  nên $\frac{6}{5}>\frac{4}{5}$

Đáp án cần chọn là: C

Câu 3: Chọn số thích hợp điền vào chỗ trống sau: $\frac{7}{23}<\frac{\mathrm{...}}{23}$

A.9

B.7

C.5

D.4

Trả lời:

7 < 9 nên $\frac{7}{23}<\frac{9}{23}$

Đáp án cần chọn là: A

Câu 4: Điền dấu thích hợp vào chỗ chấm 

$\frac{-12}{25}\mathrm{...}\frac{17}{-25}$

A. >  

B. <  

C. =  

D.Tất cả các đáp án trên đều sai

Trả lời:

 $\frac{17}{-25}=\frac{-17}{25}$

Vì -12 > -17 nên $\frac{-12}{25}>\frac{-17}{25}$ hay  $\frac{-12}{25}>\frac{17}{-25}$

Đáp án cần chọn là: A

Câu 5: Chọn câu sai

A.  $\frac{2}{-3}>\frac{-7}{8}$

B.  $\frac{-22}{33}=\frac{200}{-300}$

C.  $-\frac{2}{5}<\frac{196}{294}$

D.  $\frac{-3}{5}<\frac{39}{-65}$

Trả lời:

Đáp án A: Ta có:

$\frac{2}{-3}=\frac{-2}{3}=\frac{-2.8}{3.8}=\frac{-16}{24};\frac{-7}{8}=\frac{-7.3}{8.3}=\frac{-21}{24}$

Vì $\frac{-16}{24}>\frac{-21}{24}$ nên suy ra $\frac{2}{-3}>\frac{-7}{8}$ nên A đúng.

Đáp án B: Ta có:

 $\frac{-22}{33}=\frac{-22:11}{33:11}=\frac{-2}{3};\frac{200}{-300}=\frac{-200}{300}=\frac{-200:100}{300:100}=\frac{-2}{3}$

Vì $\frac{-2}{3}=\frac{-2}{3}$ nên suy ra $\frac{-22}{33}=\frac{200}{-300}$ nên B đúng.

Đáp án C: Ta có:

 $-\frac{2}{5}<0;\frac{196}{294}>0\Rightarrow \frac{-2}{5}<0<\frac{196}{294}\Rightarrow \frac{-2}{5}<\frac{196}{294}$nên C đúng.

Đáp án D: Ta có:

$\frac{39}{-65}=\frac{39:(-13)}{(-65):(-13)}=\frac{-3}{5}$

Vì $\frac{-3}{5}=\frac{-3}{5}$ nên suy ra $\frac{-3}{5}=\frac{39}{-65}$ nên D sai.

Đáp án cần chọn là: D

Câu 6: Điền dấu thích hợp vào chỗ chấm:  $\frac{-5}{13}\mathrm{...}\frac{-7}{13}$

A. >  

B. <    

C. =  

D.Tất cả các đáp án trên đều sai

Trả lời:

Vì – 5 > −7  nên $\frac{-5}{13}>\frac{-7}{13}$

Đáp án cần chọn là: A

Câu 7: Chọn câu đúng

A.$\frac{1123}{1125}>1$

B.$\frac{-154}{-156}<1$

C.$\frac{-123}{345}>0$

D.$\frac{-657}{-324}<0$

Trả lời:

Đáp án A: Vì 1123 < 1125 nên $\frac{1123}{1125}<1$⇒A sai.

Đáp án B: $\frac{-154}{-156}=\frac{154}{156}$

 Vì 154 < 156  nên $\frac{154}{156}<1$ hay $\frac{-154}{-156}<1$⇒B đúng.

Đáp án C:  $\frac{-123}{345}<0$ vì nó là phân số âm.⇒C sai.

Đáp án D: $\frac{-657}{-324}>0$ vì nó là phân số dương. =>D sai.

Đáp án cần chọn là: B

Câu 8: Sắp xếp các phân số $\frac{29}{41};\frac{28}{41};\frac{29}{40}$ theo thứ tự tăng dần ta được

A. $\frac{29}{41};\frac{28}{41};\frac{29}{40}$

B. $\frac{29}{40};\frac{29}{41};\frac{28}{41}$

C. $\frac{28}{41};\frac{29}{41};\frac{29}{40}$

D. $\frac{28}{41};\frac{29}{40};\frac{29}{41}$

Trả lời:

Ta có:

+) 28 < 29 nên  $\frac{28}{41}<\frac{29}{41}$

+) 41 > 40 nên  $\frac{29}{41}<\frac{29}{40}$

Do đó  $\frac{28}{41}<\frac{29}{41}<\frac{29}{40}$

Đáp án cần chọn là: C

Câu 9: Có bao nhiêu phân số lớn hơn $\frac{1}{6}$ nhưng nhỏ hơn $\frac{1}{4}$ mà có tử số là 5.

A.9 

B.10  

C.11

D.12

Trả lời:

Gọi phân số cần tìm là $\frac{5}{x}(x\in N\ast )$

Ta có:  $\frac{1}{6}<\frac{5}{x}<\frac{1}{4}$

$\Rightarrow \frac{5}{30}<\frac{5}{x}<\frac{5}{20}\Rightarrow 30>x>20$ hay  $x\in \left\{21;22;\mathrm{...};29\right\}$

 Số giá trị của xx là: (29 − 21) : 1 + 1 = 9

Vậy có tất cả 9 phân số thỏa mãn bài toán.

Đáp án cần chọn là: A

Câu 10: So sánh $\frac{2^5.7+2^5}{2^5{.5}^2-2^5.3}$ và $\frac{3^4.5-3^6}{3^4.13+3^4}$ với 1.

A. A < 1 < B

B. A = B = 1

C. A > 1 > B

D. 1 > A > B

Trả lời:

 $$\begin{gathered} \frac{2^5.7+2^5}{2^5{.5}^2-2^5.3}=\frac{2^5.(7+1)}{2^5.(5^2-3)}=\frac{2^5.(7+1)}{2^5.(25-3)}=\frac{2^5.8}{2^5.22}=\frac{8}{22}=\frac{4}{11} \\ \frac{3^4.5-3^6}{3^4.13+3^4}=\frac{3^4.(5-3^2)}{3^4.(13+1)}=\frac{3^4.(5-9)}{3^4.14}=\frac{3^4.(-4)}{3^4.14}=\frac{-4}{14}=\frac{-2}{7} \end{gathered}$$

MSC = 77

 $\frac{4}{11}=\frac{4.7}{11.7}=\frac{28}{77};\frac{-2}{7}=\frac{-2.11}{7.11}=\frac{-22}{77}$

Do đó $\frac{-22}{77}<\frac{28}{77}<1$ hay B < A < 1

Đáp án cần chọn là: D

Câu 11: Cho $A=\frac{25.9-25.17}{-8.80-8.10}$ và $B=\frac{48.12-48.15}{-3.270-3.30}$ . Chọn câu đúng.

A. A < B 

B. A = B  

C. A > 1; B < 0

D. A > B

Trả lời:

 $A=\frac{25.9-25.17}{-8.80-8.10}=\frac{25.(9-17)}{-8.(80+10)}=\frac{25.(-8)}{(-8).90}=\frac{25}{90}=\frac{5}{18}$

$B=\frac{48.12-48.15}{-3.270-3.30}=\frac{48.(12-15)}{(-3).(270+30)}=\frac{48.(-3)}{(-3).300}=\frac{48}{300}=\frac{4}{25}$

Vì A < 1  nên loại đáp án C.

So sánh A và B:

MSC = 450

$\frac{5}{18}=\frac{5.25}{18.25}=\frac{125}{450};\frac{4}{25}=\frac{4.18}{25.18}=\frac{72}{450}$

Vì 125 > 72 nên $\frac{125}{450}>\frac{72}{450}$ hay  $\frac{5}{18}>\frac{4}{25}$

Vậy A > B

Đáp án cần chọn là: D

Câu 12: Số các cặp số nguyên (x;y) thỏa mãn $\frac{1}{18}<\frac{x}{12}<\frac{y}{9}<\frac{1}{4}$ là:

A.2 

B.3  

C.1            

D.4

Trả lời:

MSC:36MSC:36

Khi đó:

$$\begin{gathered} \Rightarrow \frac{2}{36}<\frac{x.3}{36}<\frac{y.4}{36}<\frac{9}{36} \\ \Rightarrow 2<x.3<y.4<9 \end{gathered}$$

Mà (x.3) ⋮ 3  và (y.4) ⋮ 4  nên x.3 ∈ {3; 6} và y.4 ∈ {4; 8}

Mà x.3 < y.4  nên:

+ Nếu x.3 = 3 thì y.4 = 4 hoặc y.4 = 8

Hay nếu x = 1 thì y = 1  hoặc y = 2

+ Nếu x.3 = 6  thì y.4 = 8

Hay nếu x = 2  thì y = 2

Vậy các cặp số nguyên (x; y)  là (1; 1), (1; 2), (2; 2)

Đáp án cần chọn là: B

Câu 13: Tìm một phân số có mẫu là 13, biết rằng giá trị của nó không thay đổi khi ta cộng tử với −20 và nhân mẫu với 5.

A. $\frac{10}{13}$

B. $\frac{7}{13}$

C. $\frac{-5}{13}$

D. $\frac{-10}{13}$

Trả lời:

Gọi phân số cần tìm là  $\frac{a}{13}\left(a\in Z\right)$

Theo yêu cầu bài toán:

$\begin{array}{l}\frac{a}{13}=\frac{a+\left(-20\right)}{13.5}\\ \frac{a.5}{13.5}=\frac{a+\left(-20\right)}{13.5}\\ a.5=a+\left(-20\right)\\ a.5-a=-20\\ a.4=-20\\ a=\left(-20\right):4\\ a=-5\end{array}$

Vậy phân số cần tìm là $\frac{-5}{13}$

Đáp án cần chọn là: C

Câu 14: So sánh các phân số $A=\frac{3535.232323}{353535.2323}$; $B=\frac{3535}{3534}$ ; $C=\frac{2323}{2322}$

A. A < B < C 

B. A = B < C

C. A > B > C        

D. A = B = C

Trả lời:

 $$\begin{gathered} A=\frac{3535.232323}{353535.2323}=\frac{\left(35.101\right).\left(23.10101\right)}{\left(35.10101\right).\left(23.101\right)}=1 \\ B=\frac{3535}{3534}=\frac{3534+1}{3534}=\frac{3534}{3534}+\frac{1}{3534}=1+\frac{1}{3534} \\ C=\frac{2323}{2322}=\frac{2322+1}{2322}=\frac{2322}{2322}+\frac{1}{2322}=1+\frac{1}{2322} \end{gathered}$$

Vì  nên B < C

Mà B > 1 nên B > A

Vậy A < B < C

Đáp án cần chọn là: A

Câu 15: So sánh $A=\frac{{2018}^{2018}+1}{{2018}^{2019}+1}$  và  $B=\frac{{2018}^{2017}+1}{{2018}^{2018}+1}$

A. A < B

B. A = B

C. A > B

D. Không kết luận được

Trả lời:

Dễ thấy A < 1 nên:

$A=\frac{{2018}^{2018}+1}{{2018}^{2019}+1}<\frac{\left({2018}^{2018}+1\right)+2017}{\left({2018}^{2019}+1\right)+2017}=\frac{{2018}^{2018}+2018}{{2018}^{2019}+2018}=\frac{2018.\left({2018}^{2017}+1\right)}{2018.\left({2018}^{2018}+1\right)}$

$=\frac{{2018}^{2017}+1}{{2018}^{2018}+1}=B$

Vậy A < B

Đáp án cần chọn là: A

Câu 16: Chọn câu đúng

A.  $\frac{10}{11}>\frac{14}{5}$

B.  $\frac{8}{13}>\frac{5}{2}$

C.  $\frac{7}{5}>\frac{7}{8}$

D.  $\frac{1}{5}>\frac{2}{3}$

Trả lời:

Ta có:

 $\frac{10}{11}=\frac{50}{55}$và $\frac{14}{5}=\frac{154}{55}$ . Vì $\frac{50}{55}<\frac{154}{55}$ nên  $\frac{10}{11}<\frac{14}{5}$

 $\frac{8}{13}=\frac{16}{26}$và $\frac{5}{2}=\frac{65}{26}$ . Vi $\frac{16}{26}<\frac{65}{26}$ nên  $\frac{8}{13}<\frac{5}{2}$

 $\frac{7}{5}=\frac{56}{40}$ và $\frac{7}{8}=\frac{35}{40}$ . Vì $\frac{56}{40}>\frac{35}{40}$ nên  $\frac{7}{5}>\frac{7}{8}$

$\frac{1}{5}=\frac{3}{15}$ và $\frac{2}{3}=\frac{10}{15}$ . Vì  $\frac{3}{15}<\frac{10}{15}$ nên  $\frac{1}{5}<\frac{2}{3}$

Đáp án cần chọn là: C

Câu 17: C$\frac{4}{15}<\frac{7}{15}<\frac{8}{15}$họn câu đúng

A.  $\frac{6}{7}<\frac{8}{7}<\frac{7}{7}$

B.  $\frac{9}{22}<\frac{13}{22}<\frac{18}{22}$

C.  $\frac{7}{15}<\frac{8}{15}<\frac{4}{15}$

D.  $\frac{5}{11}>\frac{7}{11}>\frac{4}{11}$

Trả lời:

6 < 7 < 8 nên  $\frac{6}{7}<\frac{7}{7}<\frac{8}{7}$

9 < 13 < 18 nên $\frac{9}{22}<\frac{13}{22}<\frac{18}{22}$

4 < 7 < 8 nên  $\frac{4}{15}<\frac{7}{15}<\frac{8}{15}$

4 < 5 < 7 nên  $\frac{4}{11}<\frac{5}{11}<\frac{7}{11}$

Đáp án cần chọn là: B

Câu 18: Chọn số thích hợp điền vào chỗ trống sau:  $\frac{17}{19}<\frac{\mathrm{...}}{19}<1$

A.16

B.17

C.18

D.19

Trả lời:

Ta có:  $1=\frac{19}{19}$

17 < 18 < 19 nên $\frac{17}{19}<\frac{18}{19}<\frac{19}{19}$ hay  $\frac{17}{19}<\frac{18}{19}<1$

Đáp án cần chọn là: C

Câu 19: Lớp 6B gồm 35 học sinh có tổng chiều cao là 525 dm. Lớp 6B gồm 30 học sinh có tổng chiều cao là 456 dm. Nhận xét nào sau đây là đúng khi nói về chiều cao trung bình của các học sinh ở 2 lớp?

A.Chiều cao trung bình của các học sinh ở lớp 6A lớn hơn lớp 6B.

B.Chiều cao trung bình của các học sinh lớp 6B lớn hơn lớp 6A.

C.Chiều cao trung bình của các học sinh ở hai lớp bằng nhau.

D.Chưa đủ dữ liệu để so sánh chiều cao trung bình của học sinh ở hai lớp.

Trả lời:

Chiều cao trung bình của các học sinh ở lớp 6A là: $\frac{525}{35}$

 Chiều cao trung bình của các học sinh ở lớp 6B là: $\frac{456}{30}$

Ta có:

$\frac{525}{35}=15=\frac{75}{5}$  và $\frac{456}{30}=\frac{76}{5}$

Vì $\frac{75}{5}<\frac{76}{5}$ nên $\frac{525}{35}<\frac{456}{30}$

Vậy chiều cao trung bình của các học sinh lớp 6B lớn hơn lớp 6A.

Đáp án cần chọn là: B

Câu 20: Em hãy sắp xếp các phân số sau theo thứ tự giảm dần: $\frac{1}{4};\frac{2}{3};\frac{1}{2};\frac{4}{3};\frac{5}{2}$

A.  $\frac{4}{3}>\frac{5}{2}>\frac{2}{3}>\frac{1}{2}>\frac{1}{4}$

B. $\frac{5}{2}>\frac{4}{3}>\frac{2}{3}>\frac{1}{2}>\frac{1}{4}$  

C. $\frac{5}{2}>\frac{4}{3}>\frac{2}{3}>\frac{1}{4}>\frac{1}{2}$

D. $\frac{4}{3}>\frac{5}{2}>\frac{2}{3}>\frac{1}{4}>\frac{1}{2}$

Trả lời:

Ta có: các phân số có tử số nhỏ hơn mẫu số là các phân số nhỏ hơn 1 là: $\frac{1}{4};\frac{2}{3};\frac{1}{2}$

Quy đồng chung mẫu số các phân số này, ta được:  $\frac{1}{4}=\frac{3}{12};\frac{1}{4}=\frac{3}{12};\frac{1}{2}=\frac{6}{12}$

 Nhận thấy: $\frac{3}{12}<\frac{6}{12}<\frac{8}{12}$ suy ra  $\frac{1}{4}<\frac{1}{2}<\frac{2}{3}$

Các phân số lớn hơn , nhỏ hơn là 

Phân số lớn hơn 1 nhỏ hơn 2 là: $\frac{4}{3}$

 Phân số lớn hơn 2 là: $\frac{5}{2}$
Như vậy, sắp xếp các phân số theo thứ tự giảm dần là:

$\frac{5}{2}>\frac{4}{3}>\frac{2}{3}>\frac{1}{2}>\frac{1}{4}$

Đáp án cần chọn là: B

Câu 21: Lớp 6A có $\frac{9}{35}$ số học sinh thích bóng bàn, $\frac{3}{4}$  số học sinh thích bóng chuyền,  $\frac{4}{7}$ số học sinh thích bóng đá. Môn bóng nào được các bạn học sinh lớp 6A yêu thích nhất?

A.Môn bóng bàn.

B.Môn bóng chuyền.

C.Môn bóng đá.

D.Cả 3 môn bóng được các bạn yêu thích như nhau.

Trả lời:

Ta có :

$\frac{3}{7}=\frac{15}{35};\frac{4}{7}=\frac{20}{35}$

$\frac{9}{35}<\frac{15}{35}<\frac{20}{35}$

$\frac{9}{35}<\frac{3}{7}<\frac{4}{7}$

Vậy môn bóng đá được các bạn lớp 6A yêu thích nhất.

Đáp án cần chọn là: C

Phần 2. Lý thuyết So sánh phân số

1. So sánh hai phân số có cùng mẫu

Quy tắc 1. Với hai phân số có cùng một mẫu dương: Phân số nào có tử số nhỏ hơn thì phân số đó nhỏ hơn, phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

Ví dụ 1. So sánh .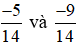

Lời giải:

Ta có −5 > −9 và 14 > 0 nên .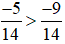

Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.

Ví dụ 2. So sánh .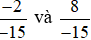

Lời giải:

Đưa hai phân số về cùng mẫu dương, ta được:

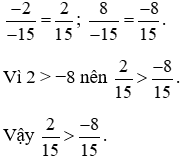
2. So sánh hai phân số khác mẫu

Quy tắc 2. Để so sánh hai phân số có mẫu khác nhau, ta viết hai phân số đó ở dạng hai phân số có cùng một mẫu dương rồi so sánh hai phân số mới nhận được.

Ví dụ 3. So sánh .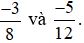

Lời giải:

Mẫu số chung = BCNN (8; 12) = 24.

Ta thực hiện 

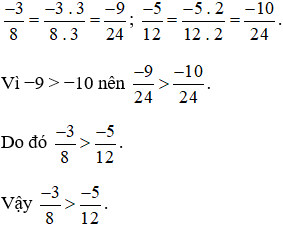
3. Áp dụng quy tắc so sánh phân số

Nhờ viết số nguyên dưới dạng phân số, ta so sánh được số nguyên với phân số.

Ví dụ 4. Viết số nguyên dưới dạng phân số rồi so sánh hai số sau: 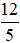 và 3.

Lời giải:

a) Ta có: .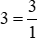

Mẫu số chung là: 5.

Ta thực hiện: 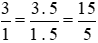 và giữ nguyên phân số .

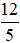Vì 15 > 12 nên

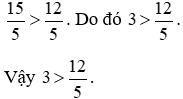
Chú ý: Khi so sánh phân số ta có thể áp dụng tính chất bắc cầu. Nghĩa là: 

Nếu có 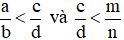 thì ta có .

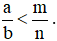Ví dụ 5. So sánh .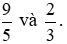

Lời giải: 

Phân số 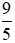 có tử số là 9 lớn hơn mẫu số là 5 nên .

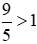Phân số 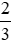 có tử số là 2 nhỏ hơn mẫu số là 3 nên .

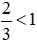Do đó .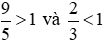

Theo tính chất bắc cầu, ta suy ra:

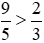
Nhận xét: 

- Phân số nhỏ hơn số 0 gọi là phân số âm. Phân số lớn hơn số 0 là phân số dương.

- Theo tính chất bắc cầu, phân số âm nhỏ hơn phân số dương.

Ví dụ 6. So sánh  .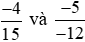

Lời giải: 

Ta có: 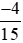 là phân số âm vì phân số có tử số và mẫu số trái dấu nên .

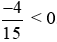Và 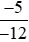 là phân số dương vì phân số có tử số và mẫu số cùng dấu nên .

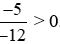Áp dụng tính chất bắc cầu, ta suy ra:  .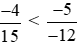

Vậy 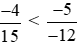.