30 câu Trắc nghiệm Phép nhân và phép chia hết hai số nguyên (có đáp án 2024) – Toán 6 Chân trời sáng tạo

Trắc nghiệm Toán lớp 6 Bài 4: Phép nhân và phép chia hết hai số nguyên

Phần 1. Trắc nghiệm Phép nhân và phép chia hết hai số nguyên

Dạng 1. Phép nhân hai số nguyên

Câu 1. Cho Q = −135.17 − 121.17 − 256.(−17), chọn câu đúng.

A. −17

B. 0

C. 1700

D. −1700

Trả lời:

Q = −135.17 − 121.17 − 256.(−17)

Q = −135.17 − 121.17 + 256.17

Q = 17.(−135 – 121 + 256)

Q = 17.(−256 + 256)

Q = 17.0

Q = 0

Đáp án cần chọn là: B

Câu 2. Chọn câu đúng.

A. (−23).(−16)  > 23.(−16)

B. (−23).(−16) = 23.(−16)   

C. (−23).(−16) < 23.(−16) 

D. (−23).16  > 23.(−6)

Trả lời:

Đáp án A: 

(−23).(−16) > 23.(−16) đúng vì VT > 0, VP < 0

Đáp án B: 

(−23).(−16) = 23.(−16) sai vì VT > 0, VP < 0 nên VT ≠ VP

Đáp án C: 

(−23).(−16) < 23.(−16) sai vì VT > 0, VP < 0 nên VT > VP

Đáp án D:

(−23).16 > 23.(−6) sai vì: (−23).16 = −368 và 23.(−6) = −138

 mà −368 < −138 nên (−23).16 < 23.(−6)

Đáp án cần chọn là: A

Câu 3. Tính hợp lý A = −43.18 − 82.43 − 43.100

A. 0  

B. −86000

C. −8600 

D. −4300

Trả lời:

A = −43.18 − 82.43 − 43.100

A = 43.(−18 – 82 − 100)

A = 43.[−(18 + 82 + 100)]

A = 43.(−200)

A = −8600

Đáp án cần chọn là: C

Câu 4. Cho (−4).(x − 3) = 20. Tìm x:

A. 8

B. −5

C. −2 

D. Một kết quả khác

Trả lời:

Vì (−4).(−5) = 4.5= 20 nên để (−4).(x−3) = 20 thì x – 3 = −5

Khi đó ta có:

x −3 = −5

x = −5 + 3

x = −2

Vậy x = −2.

Đáp án cần chọn là: C

Câu 5. Tìm x∈Z biết (1 − 3x)3  = −8.

A. x = 1

B. x = −1

C. x = −2

D. Không có x

Trả lời:

(1−3x)3 = −8

(1−3x)3 = (−2)3

1 − 3x = −2

3x = 1 − (−2)

3x = 3

x = 3:3

x =1

Vậy x = 1

Đáp án cần chọn là: A

Câu 6. Tính (−42).(−5) được kết quả là:

A. −210

B. 210

C. −47

D. 37

Trả lời:

Áp dụng quy tắc nhân hai số nguyên cùng dấu ta có:

 (−42).(−5) = 42.5 = 210

Đáp án cần chọn là: B

Câu 7. Chọn câu sai.

A. (−5).25 = −125                         

B. 6.(−15) = −90                            

C. 125.(−20) = −250                          

D. 225.(−18) = −4050

Trả lời:

Đáp án A: (−5).25 = −125 nên A đúng.

Đáp án B: 66.(−15) = −90 nên B đúng.

Đáp án C: 125.(−20) = −2500 ≠ −250 nên CC sai.

Đáp án D: 225.(−18) = −4050 nên D đúng.

Đáp án cần chọn là: C

Câu 8. Chọn câu đúng.

A. (−20).(−5) = −100

B. (−50).(−12) = 600

C. (−18).25 = −400   

D. 11.(−11) = −1111

Trả lời:

Đáp án A: (−20).(−5) = 100 nên A sai.

Đáp án B: (−50).(−12) = 600 nên B đúng.

Đáp án C: (−18).25 = −450 ≠ −400 nên C sai.

Đáp án D: 11.(−11) = −121 ≠ −1111 nên D sai.

Đáp án cần chọn là: B

Câu 9. Tích (−3).(−3).(−3).(−3).(−3).(−3).(−3) bằng

A. 38 

B. −37   

C. 37                  

D. (−3)8

Trả lời:

Ta có:

(−3).(−3).(−3).(−3).(−3).(−3).(−3)

= (−3)7

= −37

Đáp án cần chọn là: B

Câu 10. Tính nhanh (−5).125.(−8).20.(−2) ta được kết quả là

A. −200000

B. −2000000

C. 200000

D. −100000

Trả lời: (−5).125.(−8).20.(−2)

= [125.(−8)].[(−5).20].(−2)

= −(125.8).[−(5.20)].(−2)

= (−1000).(−100).(−2)

= 100000.(−2)

= −200000

Đáp án cần chọn là: A

Câu 11. Công ty Ánh Dương có lợi nhuận ở mỗi tháng trong Quý I là – 30 triệu đồng. Trong Quý II, lợi nhuận mỗi tháng của công ty là 70 triệu đồng. Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là?

A. 120 triệu

B. −120 triệu

C. 300 triệu

D. 40 triệu

Trả lời:

* Lợi nhuận Quý I là (−30).3 = −90 triệu đồng.

* Lợi nhuận Quý II là 70.3 = 210 triệu đồng.

Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là: 

(−90) + 210 = 120 triệu đồng.

Đáp án cần chọn là: A

Câu 12.

+) Tích ba số nguyên âm là một số nguyên ..(1)..

+) Tích hai số nguyên âm với một số nguyên dương là một số nguyên …(2)…

Từ thích hợp để điền vào hai chỗ chấm trên lần lượt là:

A. âm, âm

B. dương, âm

C. âm, dương

D. dương, dương

Trả lời:

Tích ba số nguyên âm là một số nguyên âm.

Tích hai số nguyên âm với một số nguyên dương là một số nguyên dương

Đáp án cần chọn là: C

Câu 13. Khẳng định nào sau đây đúng:

A. (−2).(−3).4.(−5) > 0

B. (−2).(−3).4.(−5) < 0

C. (−2).(−3).4.(−5) = 120

D. (−2).(−3).4.(−5) = 0

Trả lời:

 (−2).(−3).4.(−5)

= (−2).(−5).(−3).4

= 10.(−12)

= −120 < 0

Đáp án cần chọn là: B

 Dạng 2. Phép chia hết bội và ước của một số nguyên

Câu 1. Trong các phát biểu sau đây, phát biểu nào đúng?

A. −24 chia hết cho 5

B. 36 không chia hết cho −12

C. −18 chia hết cho −6

D. −26 không chia hết cho −13

Trả lời:

Ta có: −18 = (−6).3 nên −18 chia hết cho −6 => C đúng

Đáp án cần chọn là: C

Câu 2.  Tìm số nguyên x thỏa mãn (−9)2.x = 150 + 12.13x

A. x = 2

B. x = −2

C. x = 75                                     

D. x = −75

Trả lời:

(−9)2.x = 150 + 12.13x

81x = 150 + 156x

81x − 156x = 150

−75x = 150

x = 150:(−75)

x = −2

Đáp án cần chọn là: B

Câu 3. Nhiệt độ đầu tuần tại một trạm nghiên cứu ở Nam Cực là C−250C. Sau 7 ngày nhiệt độ tại đây là −390C. Hỏi trung bình mỗi ngày nhiệt độ thay đổi bao nhiêu độ C?

A. giảm 20C

B. tăng 20C

C. giảm 140C

D. tăng 140C

Trả lời:

Nhiệt độ thay đổi trong 7 ngày là (−39) − (−25) = −14

Nhiệt độ thay đổi trung bình mỗi ngày là −14:7 = −2

Vậy trung bình mỗi ngày nhiệt độ giảm 20C

Đáp án cần chọn là: A

Câu 4. Phát biểu nào sau đây đúng?

A. Ước của một số nguyên âm là các số nguyên âm

B. Ước của một số nguyên dương là một số nguyên dương.

C. Nếu a là bội của bb thì −a cũng là bội của bb.

D. Nếu b là ước của a thì −b là bội của aa.

Trả lời:

Ước của một số nguyên âm bao gồm cả số nguyên âm và nguyên dương => A, B sai

Nếu b là ước của a thì −b cũng là ước của a => D sai

Nếu a là bội của bb thì −a cũng là bội của b => C đúng

Đáp án cần chọn là: C

Câu 5. Số các ước nguyên của số nguyên tố p là:

A. 1

B. 2

C. 3

D. 4

Trả lời:

Số nguyên tố pp có các ước là: −1; 1; p; −p

Vậy số nguyên tố pp có 44 ước nguyên.

Đáp án cần chọn là: D

Câu 6. Các bội của 6  là:

A. −6; 6; 0; 23; −23

B. 132; −132; 16  

C. −1; 1; 6; −6  

D. 0; 6; −6; 12; −12;...

Trả lời:

Bội của 6 là số 0 và những số nguyên có dạng 6k(k∈Z∗)

Các bội của 6 là: 0; 6; −6; 12; −12;...

Đáp án cần chọn là: D

Câu 7. Tập hợp tất cả các bội của 7 có giá trị tuyệt đối nhỏ hơn 50 là:

A. {0; ±7; ±14; ±21; ±28; ±35; ±42; ±49}                         

B. {±7; ±14; ±21; ±28; ±35; ±42; ±49}                            

C. {0; 7; 14; 21; 28; 35; 42; 49}                          

D. {0; 7; 14; 21; 28; 35; 42; 49; −7; −14; −21; −28; −35; −42; −49; −56;...}

Trả lời:

Bội của 7 gồm số 0 và các số nguyên có dạng 7k, k∈Z∗

Khi đó các bội nguyên dương của 7 mà nhỏ hơn 50 là:

7; 14; 21; 28; 35; 42; 49

Vậy tập hợp các bội của 7 có giá trị tuyệt đối nhỏ hơn 50 là:

{0; ±7; ±14; ±21; ±28; ±35; ±42; ±49}                         

Đáp án cần chọn là: A

Câu 8. Cho a, b∈Z và b ≠ 0. Nếu có số nguyên q sao cho a = bq  thì

A. a là ước của b

B. b là ước của a

C. a là bội của b

D. Cả B, C đều đúng.

Trả lời:

Với a, b∈Z và b ≠ 0. Nếu có số nguyên qq sao cho a = bq  thì aa là bội của b và b là ước của a.

Đáp án cần chọn là: D

Câu 9. Tìm x, biết: 12⋮x  và x < −2

A. {−1}  

B. {−3; −4; −6; −12}      

C. {−2; −1}       

D. {−2; −1; 1; 2; 3; 4; 6; 12}

Trả lời:

Tập hợp ước của 12 là: A = {±1; ±2; ±3; ±4; ±6; ±12}

Vì x < −2 nên x∈{−3; −4; −6; −12}

Đáp án cần chọn là: B

Câu 10. Tìm x  biết: 25.x = −225

A. x = −25 

B. x = 5

C. x = −9

D. x = 9

Trả lời:

25.x = −225

x = −225:25

x = −9

Đáp án cần chọn là: C

Câu 11. Các số nguyên x thỏa mãn: −8 chia hết cho x là:

A. −1; −2; −4; −8

B. 1; −1; 2; −2; 4; −4

C. 1; 2; 4; 8

D. 1; −1; 2; −2; 4; −4; 8; −8

Trả lời:

−8 chia hết cho x => x là các ước của −8.

Suy ra x∈{1; −1; 2; −2; 4; −4; 8; −8}

Đáp án cần chọn là: D

Dạng 3. Các dạng toán về phép nhân và phép chia hai số nguyên

Câu 1. Cho B = (−8).25.(−3)2 và C = (−30).(−2)3.(53) . Chọn câu đúng.

A. 3.B = 50.C

B. B.50 = C.(−3)

C. B.60 = −C

D. C = −B

Trả lời:

B = (−8).25.(−3)2

= −200.9

= −1800

C = (−30).(−2)3.(53)

= (−30).(−8).125

= (−30).(−1000)

= 30000

Khi đó:

 B.50 = −1800.50 = −90000;

C.(−3) = 30000.(−3) = −90000

Vậy B.50 = C.(−3)

Đáp án cần chọn là: B

Câu 2. Có bao nhiêu giá trị x nguyên dương thỏa mãn (x − 3).(x + 2) = 0 là:

A. 3

B. 2

C. 0

D. 1

Trả lời:

 (x − 3).(x + 2) = 0

TH1:

x – 3 = 0

x = 0 + 3

x = 3(TM)

TH2:

x + 2 = 0

x = 0 – 2

x = −2(L)

Vậy có duy nhất 1 giá trị nguyên dương của xx thỏa mãn là x = 3

Đáp án cần chọn là: D

Câu 3. Tìm x biết 2(x − 5) − 3(x − 7) = −2.

A. x = 13

B. x = 5  

C. x = 7 

D. x = 6

Trả lời:

2(x − 5) − 3(x − 7) = −2

2x – 10 − 3.x + 3.7 = −2

2x – 10 − 3x + 21 = −2

(2x − 3x) + (21 − 10) = −2

(2 − 3)x + 11 = −2

−x + 11 = −2

−x = −2 − 11

−x = −13

x = 13

Đáp án cần chọn là: A

Câu 4. Có bao nhiêu giá trị x thỏa mãn (x − 6)(x2 + 2) = 0?

A. 0

B. 2    

C. 3 

D. 1

Trả lời:

 (x − 6)(x2 + 2) = 0

Vì x2 ≥ 0 với mọi x nên x2 + 2 ≥ 0 + 2 = 2 hay x2 + 2 > 0 với mọi x

Suy ra:

 x – 6 = 0

x = 0 + 6

x = 6

Vậy chỉ có 1 giá trị của x thỏa mãn là x = 6

Đáp án cần chọn là: D

Câu 5. Cho A = (135 − 35).(−47) + 53.(−48 − 52) và B = 25.(75 − 49) + 75.|25 − 49|.

Chọn câu đúng.

A. A và B đối nhau

B. A và B bằng nhau

C. A và B cùng dấu                 

D. A và B trái dấu

Trả lời:

A = (135 − 35).(−47) + 53.(−48 − 52)

= 100.(−47) + 53.(−100)

= (−100).47 + 53.(−100)

= (−100).(47 + 53)

= (−100).100

= −10000

Vì 25 − 49 < 0 nên |25−49| = −(25 − 49) = 49 − 25

B = 25.(75 − 49) + 75.|25 − 49|

= 25.(75 − 49) + 75.(49 − 25)

= 25.75 − 25.49 + 75.49 − 75.25

= (25.75 − 75.25) + (−25.49 + 75.49)

= 0 + 49.(−25 + 75)

= 49.50

= 2450

Do đó A và B là hai số nguyên trái dấu.

Đáp án cần chọn là: D

Câu 6. Kết quả của phép tính (−125).8 là:

A. 1000

B. −1000

C. −100

D. −10000

Trả lời:

 (−125).8 = −(125.8) = −1000

Đáp án cần chọn là: B

Câu 7. Khi x = −12 , giá trị của biểu thức (x − 8).(x + 7) là số nào trong bốn số sau:

A. −100

B. 100  

C. −96

D. −196

Trả lời:

Thay x = −12 vào biểu thức (x − 8).(x + 7), ta được:

(−12 − 8).(−12 + 7)

= (−20).(−5)

= 20.5

= 100

Đáp án cần chọn là: B

Câu 8. Giá trị biểu thức M = (−192873).(−2345).(−4)5.0  là

A. −192873

B. 1

C. 0

D. (−192873).(−2345).(−4)5

Trả lời:

Vì trong tích có một thừa số bằng 0 nên M = 0

Đáp án cần chọn là: C

Câu 9. Tính giá trị biểu thức P = (−13)2.(−9) ta có

A. 117

B. −117 

C. 1521

D. −1521

Trả lời:

P = (−13)2.(−9) = 169.(−9) = −1521

Đáp án cần chọn là: D

Câu 10. Tính giá trị biểu thức P = (x − 3).3 − 20.x  khi x=5.

A. −94                            

B. 100

C. −96       

D. −104

Trả lời:

Thay x = 5 vào P ta được:

P = (5 − 3).3 − 20.5

= 2.3 – 100

= 6 – 100

= −94

Đáp án cần chọn là: A

Câu 11. Số cặp số nguyên (x; y) thỏa mãn x.y = −28 là:

A. 3  

B. 6   

C. 8  

D. 12

Trả lời:

Vì −28 = −1.28 = 1.(−28) = −2.14 = 2.(−14) = −4.7 = 4.(−7)

Nên ta có các bộ (x; y) thỏa mãn bài toán là:

(−1;28),(28;−1), (1;−28),(−28;1), (−2;14),(14;−2), (2;−14),(−14;2), (−4;7),(7;−4),  (4;−7),(−7;4).

Có tất cả 12 bộ số (x;y) thỏa mãn bài toán.

Đáp án cần chọn là: D

Câu 12. Giá trị nhỏ nhất của biểu thức 3(x + 1)2 + 7 là

A. 0 

B. 7

C. 10

D. −7

Trả lời:

Ta có:

(x + 1)2 ≥ 0 với mọi x

⇒ 3.(x + 1)2 ≥ 0 với mọi x

⇒ 3(x + 1)2 + 7 ≥ 0 + 7

⇒ 3(x + 1)2 + 7 ≥ 7

Vậy GTNN của biểu thức là 7 đạt được khi x = −1.

Đáp án cần chọn là: B

Câu 13. Tính giá trị của biểu thức: A = ax – ay + bx − by biết a + b = −5; x – y = −2

A. 7

B. 10

C. −7

D. −3

Trả lời:

A = ax – ay + bx − by

= (ax − ay) + (bx − by)

= a.(x − y) + b.(x − y)

= (a + b).(x − y)

Thay a + b = −5; x – y = −2  ta được:

A = (−5).(−2) = 10

Đáp án cần chọn là: B

Câu 14. Tìm x∈Z biết (x + 1) + (x + 2) +...+ (x + 99) + (x + 100) = 0

A. 90,6

B. Không có x thỏa mãn.    

C. 50,5           

D. −50,5

Trả lời:

 (x + 1) + (x + 2) +...+ (x + 99) + (x + 100) = 0

(x + x +....+ x) + (1 + 2 +...+ 100) = 0

100x + (100 + 1).100:2 = 0

100x + 5050 = 0

100x = −5050

x = −50,5

Mà x∈Z nên không có x thỏa mãn.

Đáp án cần chọn là: B

Câu 15. Có bao nhiêu cặp số x; y∈Z thỏa mãn xy + 3x − 7y = 23?

A. 1

B. 2

C. 3

D. 4

Trả lời:

xy + 3x − 7y – 23 = 0

xy + 3x − 7y – 21 − 2= 0

x(y + 3) − 7(y + 3) = 2

(x − 7)(y + 3) = 2

Ta có các trường hợp:

x-7	1	2	-1	-2
x	8	9	6	5
x+3	2	1	-2	-1
y	-1	-2	-5	-4

Vậy các cặp số (x, y) là {(8; −1); (9; −2); (6; −5); (−5; −4)}

Vậy có 4 cặp số thỏa mãn bài toán.

Đáp án cần chọn là: D

Câu 16. Giá trị biểu thức: 15x − 23 với x = −1 là:

A. −8

B. 8

C. 38

D. −38

Trả lời:

Thay x = −1 vào biểu thức ta được:

15.(−1)−23 = (−15)−23 = (−15)+(−23) = −38

Đáp án cần chọn là: D

Câu 17. Công ty Ánh Dương có lợi nhuận ở mỗi tháng trong Quý I là – 30 triệu đồng. Trong Quý II, lợi nhuận mỗi tháng của công ty là 70 triệu đồng. Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là?

A. 120 triệu

B. −120 triệu

C. 300 triệu

D. 40 triệu

Trả lời:

* Lợi nhuận Quý I là (−30).3 = −90 triệu đồng.

* Lợi nhuận Quý II là 70.3 = 210 triệu đồng.

Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là:

(−90)+210=120 triệu đồng.

Đáp án cần chọn là: A

Câu 18. Giá trị nào dưới đây của xx thỏa mãn −6(x + 7) = 96?

A. x = 95                               

B. x = −16                                  

C. x = −23  

D. x = 96

Trả lời:

−6(x + 7) = 96

x + 7= 96:(−6)

x + 7= −16

x = −16 − 7

x = −23

Đáp án cần chọn là: C

Câu 19. Có bao nhiêu cặp số (x; y) nguyên biết: (x − 1)(y + 1) = 3?

A. 1

B. 3

C. 2

D. 4

Trả lời:

Ta có: 3 = 1.3 = 3.1 = (−1).(−3) = (−3).(−1)

Ta có bảng:

x-1	1	3	-1	-3
y+1	3	1	-3	-1
(x;y)	x= 2;y = 2	x = 4; y = 0	x = 0;y = -4	x = -2;y = -2

Vậy có 4 cặp số (x; y) thỏa mãn là:

 (2;2), (4;0), (0;−4), (−2;−2)

Đáp án cần chọn là: D

Câu 20. Bạn Hồng đang ngồi trên máy bay, bạn ấy thấy màn hình thông báo nhiệt độ bên ngoài máy bay là −280C. Máy bay đang hạ cánh, nhiệt độ bên ngoài trung bình mỗi phút tăng lên 40C. Hỏi sau 10 phút nữa nhiệt độ bên ngoài máy bay là bao nhiêu độ C?

A. 240C

B. 120C

C. – 240C

D. 120C

Trả lời:

Nhiệt độ bên ngoài sau 10 phút là:

 −28 + 10.4 = −28 + 40 = 120C

Đáp án cần chọn là: D

Dạng 4. Các dạng toán về phép nhân và phép chia hết hai số nguyên (tiếp)

Câu 1. Cho x∈Z và (−154 + x)⋮3 thì:

A. x  chia 3 dư 1                        

B. x⋮3                     

C. x chia 3 dư 2                  

D. không kết luận được tính chia hết cho 3 của x

Trả lời:

Ta có:

(−154 + x)⋮3

(−154 + x)⋮3

(−153 – 1 + x)⋮3

(−153 – 1 + x)⋮3

Suy ra (x − 1)⋮3 (do −153⋮3)

Do đó x – 1 = 3k ⇒ x = 3k + 1

Vậy x chia cho 3 dư 1.

Đáp án cần chọn là: A

Câu 2. Tìm n∈Z, biết: (n + 5)⋮(n + 1)

A. n∈{±1; ±2; ±4} 

B. n∈{−5; −3; −2; 0; 1; 3}                                  

C. n∈{0; 1; 3}                                     

D. n∈{±1; ±5}

Trả lời:

 (n + 5)⋮(n + 1) ⇒ (n + 1) + 4⋮(n + 1)

Vì n+1⋮n+1 và n∈Z nên để n+5⋮n+1 thì 4⋮n+1

Hay n+1∈U(4) = {±1;±2;±4}

Ta có bảng:

n+1	1	-1	2	-2	4	-4
n	0	-2	1	-3	3	-5

Vậy n∈{−5;−3;−2;0;1;3}

Đáp án cần chọn là: B

Câu 3. Có bao nhiêu số nguyên a < 5 biết: 10 là bội của (2a + 5)

A. 4                               

B. 5      

C. 8

D. 6

Trả lời:

Vì 10 là bội của 2a+5 nên 2a+5 là ước của 10

U(10) = {±1; ±2; ±5; ±10}

Ta có bảng:

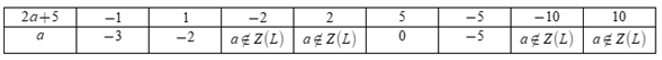
Mà a < 5 nên a∈{−3; −2; 0; −5}

Vậy có 4 giá trị nguyên của a thỏa mãn bài toán.

Đáp án cần chọn là: A

Câu 4. Tìm x, biết: x⋮6 và 24⋮x

A. x∈{±6; ±24}

B. x∈{±6; ±12; ±24}     

C. x∈{±6; ±12}                                     

D. {±6; ±12; ±8; ±24}

Trả lời:

Ta có:

A = B(6) = {0; ±6; ±12; ±18; ±24;...}

B = Ư(24) = {±1; ±2; ±3; ±4; ±6; ±8; ±12; ±24}

Vậy x∈A∩B = {±6; ±12; ±24}

Đáp án cần chọn là: B

Câu 5. Cho a và b là hai số nguyên khác 0. Biết a⋮b và b⋮a. Khi đó

A. a = b                               

B. a = −b                                  

C. a = 2b                                     

D. Cả A, B đều đúng

Trả lời:

Ta có:

a⋮b ⇒ a = b.q1(q1∈Z)

b⋮a ⇒ b = a.q2(q2∈Z)

Suy ra a = b.q1 = (a.q2).q1 = a. (q1q2)

Vì a ≠ 0 nên a=a(q1q2) ⇒ 1 = q1q2

Mà q1,q2∈Z

 nên q1 = q2 = 1 hoặc q1 = q2 = −1

Do đó a = b hoặc a = −b

Đáp án cần chọn là: D

Câu 6. Chọn câu sai.

A. (−19).(−7) > 0

B. 3.(−121) < 0

C. 45.(−11) < −500  

D. 46.(−11) < −500

Trả lời:

Đáp án A: (−19).(−7) > 0  đúng vì tích hai số nguyên cùng dấu là một số nguyên dương.

Đáp án B: 3.(−121) < 0 đúng vì tích hai số nguyên khác dấu là một số nguyên âm.

Đáp án C: 45.(−11) = −495 > −500 nên C sai.

Đáp án D: 46.(−11) = −506 < −500 nên D đúng.

Đáp án cần chọn là: C

Câu 7. Có bao nhiêu số nguyên x thỏa mãn (x − 7)(x + 5) < 0?

A. 4

B. 11

C. 5

D. Không tồn tại x

Trả lời:

(x − 7)(x + 5) < 0 nên x − 7 và x + 5 khác dấu.

Mà x + 5 > x − 7 nên x + 5 > 0 và x – 7 < 0

Suy ra x > −5 và x < 7

Do đó x∈{−4,−3,−2,−1,0,1,2,3,4,5,6}

Vậy có 11 giá trị nguyên của x thỏa mãn bài toán.

Đáp án cần chọn là: B

Câu 8. Tập hợp các ước của −8 là:

A. A = {1; −1; 2; −2; 4; −4; 8; −8}                    

B. A = {0; ±1; ±2; ±4; ±8}                  

C. A = {1; 2; 4; 8}                                                        

D. A = {0; 1; 2; 4; 8}

Trả lời:

Ta có: −8 = −1.8 = 1.(−8) = −2.4 = 2.(−4)

Tập hợp các ước của −8 là: A = {1; −1; 2; −2; 4; −4; 8; −8}                    

Đáp án cần chọn là: A

Câu 9. Có bao nhiêu ước của −24.

A. 9

B. 17

C. 8

D. 16

Trả lời:

Có 8 ước tự nhiên của 24 là: 1; 2; 3; 4; 6; 8; 12; 24

Có 8 ước nguyên âm của 24 là: −1; −2; −3; −4; −6; −8; −12; −24

Vậy có 8.2 = 16 ước của 24 nên cũng có 16 ước của −24.

Đáp án cần chọn là: D

Câu 10. Giá trị lớn nhất của a thỏa mãn a + 4 là ước của 9 là:

A. a = 5

B. a = 13

C. a = −13  

D. a = 9

Trả lời:

a + 4 là ước của 9
⇒ (a + 4)∈U(9) = {±1; ±3; ±9}

Ta có bảng giá trị như sau:

a + 4	1	-1	3	-3	9	-9
a	-3	-5	-1	-7	5	-13

Vậy giá trị lớn nhất của aa là a = 5

Đáp án cần chọn là: A

Câu 11. Gọi A là tập hợp các giá trị n∈Z để (n2 − 7) là bội của (n + 3). Tổng các phần tử của A bằng:

A. −12                               

B. −10                                  

C. 0                                     

D. −8

Trả lời:

Ta có:n2 – 7 = n2 + 3n − 3n – 9 + 2

= n(n + 3) − 3(n + 3) + 2

= (n − 3)(n + 3) + 2

Vì n∈Z nên để n2 − 7 là bội của n + 3 thì 2 là bội của n + 3 hay n + 3 là ước của 2

Ư(2) = {±1; ±2} nên n +3∈{±1; ±2}

Ta có bảng:

n + 3	1	-1	2	-2
n	-2	-4	-1	-5

Vậy n∈A = {−5; −4; −2; −1}

Do đó tổng các phần tử của A là (−5) + (−4) + (−2) + (−1) = −12

Đáp án cần chọn là: A

Câu 12. Cho x; y∈Z.  Nếu 5x + 46y chia hết cho 16  thì x + 6y chia hết cho

A. 6                               

B. 46                                  

C. 16   

D. 5

Trả lời:

Ta có:

5x + 46y= 5x + 30y + 16y = (5x + 30y) + 16y = 5(x + 6y) + 16y

Vì 5x + 46y chia hết cho 16  và 16y chia hết cho 1616 nên suy ra 5(x + 6y) chia hết cho 16.

Mà 5  không chia hết cho 16 nên suy ra x+6y chia hết cho 16

Vậy nếu 5x + 46y chia hết cho 16 thì x + 6y cũng chia hết cho 16.

Đáp án cần chọn là: C

Câu 13. Có bao nhiêu số nguyên nn thỏa mãn (n − 1) là bội của (n + 5) và (n + 5) là bội của (n − 1)? 

A. 0

B. 2

C. 1

D. 3

Trả lời:

Vì (n−1) là bội của (n+5) và (n+5) là bội của n−1,

Nên n−1 khác 0 và n+5 khác 0

Nên n+5, n−1 là hai số đối nhau

Do đó:

 (n + 5) + (n − 1) = 0

2n + 5 – 1 = 0

2n + 4 = 0

2n = −4

n = −2

Vậy có 1 số nguyên n thỏa mãn bài toán.

Đáp án cần chọn là: C

Câu 14. Trong các phát biểu sau đây, phát biểu nào đúng?

A. −24 chia hết cho 5

B. 36 không chia hết cho −12

C. −18 chia hết cho −6

D. −26 không chia hết cho −13

Trả lời:

Ta có: −18 = (−6).3 nên −18 chia hết cho −6 => C đúng

Đáp án cần chọn là: C

Phần 2. Lý thuyết Phép nhân và phép chia hết hai số nguyên

1. Nhân hai số nguyên khác dấu

Quy tắc nhân hai số nguyên khác dấu

− Tích của hai số nguyên khác dấu luôn luôn là một số nguyên âm.

− Khi nhân hai số nguyên khác dấu, ta nhân số dương với số đối của số âm rồi thêm dấu trừ (−) trước kết quả nhận được.

Chú ý: Cho hai số nguyên dương a và b, ta có:

(+ a) . (−b) = − a . b

(− a) . (+ b) = − a . b

Ví dụ: Tính:

a) (−9) . 4;

b) 6 . (−11);

c) (−14) . 50.

Hướng dẫn giải

a) (−9) . 4 = −(9.  4) = − 36;

b) 6 . (−11) = − (6 . 11) = −66;

c) (−14) . 50 = − (14 . 50) = − 700.

2. Nhân hai số nguyên cùng dấu

Quy tắc nhân hai số nguyên cùng dấu

− Khi nhân hai số nguyên cùng dương, ta nhân chúng như nhân hai số tự nhiên.

− Khi nhân hai số nguyên cùng âm, ta nhân hai số đối của chúng.

Chú ý:

• Cho hai số nguyên dương a và b, ta có: (−a) . (−b) = (+a) . (+b) = a . b.

• Tích của hai số nguyên cùng dấu luôn luôn là một số nguyên dương.

Ví dụ: Tính:

a) 15 . 6;

b) (−55) . (−10);

c) (+22) . (+11).

Hướng dẫn giải

a) 15 . 6 = 90;

b) (−55) . (−10) = 55 . 10 = 550;

c) (+22) . (+11) = 22 . 11 = 242.

3. Tính chất của phép nhân các số nguyên

a) Tính chất giao hoán

Phép nhân hai số nguyên có tính chất giao hoán, nghĩa là:

a . b = b . a

Chú ý:

• a . 1 = 1 . a = a;

• a . 0 = 0 . a = 0.

• Cho hai số nguyên x, y:

Nếu x . y = 0 thì x = 0 hoặc y = 0.

Ví dụ: Nếu (a + 5) . (a – 14) = 0 thì

a + 5 = 0 hoặc a – 14 = 0.

Suy ra a = –5 hoặc a = 14.

b) Tính chất kết hợp

Phép nhân các số nguyên có tính chất kết hợp:

(a . b) . c = a . (b . c)

Chú ý: Áp dụng tính chất kết hợp của phép nhân, ta có thể viết tích của nhiều số nguyên:

a . b . c = a . (b . c) = (a . b) . c.

Ví dụ:

[(−4) . (−5)] . 8 = (−4) . [(−5) . 8]

= (−4) . (−5) . 8 = 4 . 5 . 8

= 20 . 8 = 160.

c) Tính chất phân phối của phép nhân đối với phép cộng

Phép nhân số nguyên có tính chất phân phối đối với phép cộng:

a(b + c) = ab + ac

Phép nhân số nguyên có tính chất phân phối đối với phép trừ:

a(b − c) = ab – ac

Ví dụ: Thực hiện phép tính:

(−5) . 29 + (−5) . (−99) + (−5) . (−30).

Hướng dẫn giải

(−5) . 29 + (−5) . (−99) + (−5) . (−30)

= (−5) . [29 + (−99) + (−30)]

= (−5) . [(−70) + (−30)]

= (−5) . (−100)

= 5 . 100

= 500.

4. Quan hệ chia hết và phép chia trong tập hợp số nguyên

Cho $a,b\in \mathrm{\mathbb{Z}}$ và b ≠ 0. Nếu có số nguyên q sao cho a = bq thì

• Ta nói a chia hết cho b, kí hiệu là a ⋮ b.

• Trong phép chia hết, dấu của thương hai số nguyên cũng giống như dấu của tích.

Ta gọi q là thương của phép chia a cho b, kí hiệu là a : b = q.

Ví dụ: Ta có: (−15) = 3 . (−5) nên ta nói:

• (−15) chia hết cho (−5);

• (−15) : (−5) = 3;

• 3 là thương của phép chia (−15) cho (−5).

5. Bội và ước của một số nguyên

Cho $a,b\in \mathrm{\mathbb{Z}}$ . Nếu a ⋮ b thì ta nói a là bội của b là b là ước của a.

Ví dụ: Ta có (−15) ⋮ (−5) nên ta nói (−15) là bội của (−5) và (−5) là ước của (−15).

Nếu c vừa là ước của a, vừa là ước của b thì c cũng được gọi là ước chung của a và b.

Ví dụ: Vì 4 vừa là ước của 8 vừa là ước của 12 nên 4 là ước chung của 8 và 12.