30 câu Trắc nghiệm Số thập phân (có đáp án 2024) – Toán 6 Chân trời sáng tạo

Trắc nghiệm Toán lớp 6 Bài 1: Số thập phân

Phần 1. Trắc nghiệm Số thập phân

Câu 1: Viết các số sau theo thứ tự giảm dần:

−120,341; 36,095; 36,1; −120,34.

A. 36,095 > 36,100 > −120,34 > −120,341

B. 36,095 > 36,100 > −120,341 > −120,34

C. 36,100 > 36,095 > −120,341 > −120,34

D. 36,100 > 36,095 > −120,34 > −120,341

Trả lời:

Ta có: 36,100 > 36,095 nên 36,1 > 36,095.

−120,340 > −120,341  nên  −120,34 > −120,341

 ⇒ 36,100 > 36,095 >  −120,34 > − 120,341.

Đáp án cần chọn là: D

Câu 2: Viết các số thập phân sau dưới dạng phân số tối giản:

 −0,125  =…;  −0,012 =...; −4,005 =...

A.  $\frac{-1}{8};\frac{-3}{250};\frac{-4005}{1000}$

B.  $\frac{-1}{8};\frac{-3}{25};\frac{-801}{200}$

C.  $\frac{-1}{4};\frac{-3}{250};\frac{-801}{200}$
D.  $\frac{-1}{8};\frac{-3}{250};\frac{-801}{200}$

Trả lời:

 $$\begin{gathered} -\mathrm{0,125}=\frac{-125}{1000}=\frac{-125:125}{1000:125}=\frac{-1}{8} \\ -\mathrm{0,012}=\frac{-12}{1000}=\frac{-12:4}{1000:4}=\frac{-3}{250} \\ -\mathrm{4,005}=\frac{-4005}{1000}=\frac{-4005:5}{1000:5}=\frac{-801}{200} \end{gathered}$$

Đáp án cần chọn là: D

Câu 3: Điền dấu '>; <; =' vào ô trống

508,99  .....  509,01 

Trả lời:

Ta có: 508 < 509 nên 508,99 <  509,01.

Câu 4:  

Trong một cuộc thi chạy 200 m, có ba vận động viên đạt thành tích cao nhất là:

Mai Anh: 31,42 giây; Ngọc Mai: 31,48 giây; Phương Hà: 31,09 giây.

Các vận động viên đã về Nhất, về Nhì, về Ba lần lượt là:

A.Ngọc Mai, Mai Anh, Phương Hà.

B.Ngọc Mai, Phương Hà, Mai Anh.

C.Phương Hà, Mai Anh, Ngọc Mai.

D.Mai Anh, Ngọc Mai, Phương Hà.

Trả lời:

Ta có: 31,48 > 31,42 > 31,09.

Suy ra Ngọc Mai về nhất, Mai Anh về nhì, Phương Hà về ba.

Đáp án cần chọn là: A

Câu 5: Số đối của các số thập phân sau lần lượt là: 9,32; −12,34; −0,7; 3,333

A. 9,32; −12,34; −0,7; 3,333

B. −9,32; 12,34; 0,7; 3,333

C. −9,32; 12,34; 0,7; −3,333

D. −9,32; −12,34; 0,7; −3,333

Trả lời:

Số đối của 9,32 là −9,32

Số đối của −12,34 là 12,34

Số đối của −0,7 là 0,7

Số đối của 3,333 là  −3,333

Vậy ta được: −9,32; 12,34; 0,7; −3,333.

Đáp án cần chọn là: C

Câu 6: Viết phân số $\frac{4}{3}$ dưới dạng hỗn số ta được

A.  $1\frac{2}{3}$

B.  $3\frac{1}{3}$

C.  $3\frac{1}{4}$

D.  $1\frac{1}{3}$

Trả lời:

Ta có: 4 : 3 bằng 1 (dư 1 ) nên $\frac{4}{3}=1\frac{1}{3}$

Đáp án cần chọn là: D

Câu 7: Hỗn số $-2\frac{3}{4}$ được viết dưới dạng phân số là

A.  $-\frac{21}{4}$

B.  $-\frac{11}{4}$

C.  $-\frac{10}{4}$

D.  $-\frac{5}{4}$

Trả lời:

 $-2\frac{3}{4}=-\frac{2.4+3}{4}=-\frac{11}{4}$

Đáp án cần chọn là: B

Câu 8: Viết phân số $\frac{131}{1000}$ dưới dạng  số thập phân ta được

A.0,131 

B.0,1331  

C.1,31

D.0,0131

Trả lời:

 $\frac{131}{1000}=\mathrm{0,131}$

Đáp án cần chọn là: A

Câu 9: Viết số thập phân 0,25 về dạng phân số ta được

A.  $\frac{1}{4}$

B.  $\frac{5}{2}$

C.  $\frac{2}{5}$

D.  $\frac{1}{5}$

Trả lời:

 $\mathrm{0,25}=\frac{25}{100}=\frac{1}{4}$

Đáp án cần chọn là: A

Câu 10: Viết các phân số và hỗn số sau dưới dạng số thập phân:

$\frac{-9}{1000}=\mathrm{...};\frac{-5}{8}=\mathrm{...};3\frac{2}{25}=\mathrm{...}$

A. −0,09; −0,625; 3,08

B. −0,009; −0,625; 3,08

C. −0,9; −0,625; 3,08

D. −0,009; −0,625; 3,008

Trả lời:

 $$\begin{gathered} \frac{-9}{1000}=-\mathrm{0,009} \\ \frac{-5}{8}=\frac{-5.125}{8.125}=\frac{-625}{1000}=-\mathrm{0,625} \\ 3\frac{2}{25}=3\frac{8}{100}=\mathrm{3,08} \end{gathered}$$

Đáp án cần chọn là: B

Câu 11: Các phân số $\frac{69}{1000};8\frac{77}{100};\frac{34567}{{10}^4}$ được viết dưới dạng số thập phân theo lần lượt là

A. 0,69; 0,877; 3,4567 

B. 0,69; 8,77; 3,4567

C. 0,069; 0,877; 3,4567 

D. 0,069; 8,77; 3,4567

Trả lời:

 $\begin{array}{l}\frac{69}{1000}=\mathrm{0,069}\\ 8\frac{77}{100}=\frac{877}{100}=\mathrm{8,77}\\ \frac{34567}{{10}^4}=\mathrm{3,4567}\end{array}$

Vậy các số thập phân viết theo thứ tự là 0,069;8,77;3,4567

Đáp án cần chọn là: D

Phần 2. Lý thuyết Số thập phân

1. Số thập phân âm

- Phân số thập phân là phân số có mẫu số là lũy thừa của 10.

Ví dụ 1. Các phân số 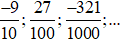 là các phân số thập phân.

- Các phân số thập phân dương được viết dưới dạng số thập phân dương.

- Các phân số thập phân âm được viết dưới dạng số thập phân âm.

Ví dụ 2.

0,332; 12,412 là các số thập phân dương.

−3,712; −4,15 là các số thập phân âm.

Số thập phân gồm hai phần:

- Phần số nguyên viết bên trái dấu phẩy;

- Phần thập phân viết bên phải dấu phẩy.

Ví dụ 3. 

- Số 42,25 là số thập phân dương có phần số nguyên là 42 và phần thập phân là 25.

- Số −12,316 là số thập phân âm có phần số nguyên là −12 và phần thập phân là 316.

2. Số đối của một số thập phân

Hai số thập phân gọi là đối nhau khi chúng biểu diễn hai phân số thập phân đối nhau.

Ví dụ 4. 

- Số đối của 3,45 là −3,45;

- Số đối của −2,36 là 2,36.

3. So sánh hai số thập phân

- Nếu hai số thập phân trái dấu, số thập phân dương lớn hơn số thập phân âm.

- Trong hai số thập phân âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.

Ví dụ 5. Sắp xếp các số thập phân theo thứ tự tăng dần:

−16,25; 8,36; −21,4; 7,24.

Lời giải:

Để sắp xếp các số thập phân sau theo thứ tự tăng dần, ta thực hiện:

Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.

Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:

- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.

- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.

Sắp xếp các số thập phân sau theo thứ tự tăng dần:

* Phân loại:

- Nhóm các số thập phân dương: 8,36; 7,24.

-  Nhóm các số thập phân âm: −16,25; −21,4.

* So sánh các số thập phân trong theo nhóm: 

- Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên, vì 8 > 7 nên 8,36 > 7,24.

-  Nhóm các số thập phân âm: Số đối của các số −16,25; −21,4 lần lượt là 16,25; 21,4.

Ta so sánh phần nguyên của hai số 16,25 và 21,4, vì 16 < 21 nên 16,25 < 21,4.

Hay −16,25 > −21,4.

Do đó −21,4 < −16,25 < 7,24 < 8,36.

Vậy các số được sắp xếp thứ tự tăng dần là: −21,4; −16,25; 7,24; 8,36.