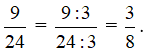30 câu Trắc nghiệm Ước chung, Ước chung lớn nhất (có đáp án 2024) – Toán 6 Chân trời sáng tạo

Trắc nghiệm Toán lớp 6 Bài 12: Ước chung. Ước chung lớn nhất

Phần 1. Trắc nghiệm Ước chung. Ước chung lớn nhất

Dạng 1. Ước chung, ước chung lớn nhất

Câu 1. Sau khi phân tích 45, 150 ra các thừa số nguyên tố được 45 = 32.5 và

150 = 2.3.52 . Số mũ nhỏ nhất của thừa số chung 3 là

A. 1

B. 2

C. 3

D. 0

Trả lời:

45 = 32.5 nên số mũ của 3 là 2

150 = 2.3.52 nên số mũ của 3 là 1

Số nhỏ nhất là 1 nên số mũ nhỏ nhất của thừa số chung 3 khi phân tích 45 và 150 ra tích các thừa số nguyên tố là 1.

Đáp án cần chọn là: A

Câu 2. Phân số $\frac{16}{10}$ được rút gọn về phân số tối giản là:

A. $\frac{16}{10}$

B. $\frac{8}{5}$

C. 2

D.$\frac{4}{5}$

Trả lời:

ƯC(15; 10) = 2. Ta chia cả tử và mẫu của $\frac{16}{10}$ cho 2 được:$\frac{16}{10}=\frac{16:2}{10:2}=\frac{8}{5}$

Đáp án cần chọn là: B

Câu 3. Sau khi phân tích 45, 150 ra các thừa số nguyên tố. Tất cả các thừa số chung của hai số này là:

A. 2 và 3

B. 2 và 5

C. 3 và 5

D. 5

Trả lời:

45 = 32.5có hai thừa số nguyên tố là 3 và 5

150 = 2.3.52 có 3 thừa số nguyên tố là 2, 3 và 5.

Các thừa số chung là 3 và 5.

Đáp án cần chọn là: C

Câu 4. Tìm ước chung của 9 và 15.

A. {1;3}

B. {0;3}

C. {1;5}

D. {1;3;9}

Trả lời:

- Ta có:

Ư(9) = {1,3,9} và Ư(15) = {1,3,5,15}

Vậy ƯC(9,15) = Ư(9)∩ Ư(15) = {1,3}

Đáp án cần chọn là: A

Câu 5. Viết các tập hợp Ư(6); Ư(20); ƯC(6,20).

A. Ư(6) = {1, 2, 3, 6}; Ư(20) = {1, 2, 4, 5, 10, 20}; ƯC(6,20) = {1, 2}

B. Ư(6) = {1,2,3,6}; Ư(20) = {1,2,4,5,20}; ƯC(6,20) = {1,2}

C. Ư(6) = {1,2,3}; Ư(20) = {1,2,4,5,10,20}; ƯC(6,20) = {1,2}

D. Ư(6) = {1,2,4,6}; Ư(20) = {1,2,4,20}; ƯC(6,20) = {1,2,4}

Trả lời:

Ta có:

Ư(6) ={1,2,3,6} và Ư(20) ={1,2,4,5,10,20}

Vậy ƯC(6,20) ={1,2}

Đáp án cần chọn là: A

Câu 6. Số x là ước chung của số a và số b nếu:

A. x∈Ư(a) và x∈B(b)

B. x⊂Ư(a)và x⊂Ư(b)

C. x∈Ư(a) vàx∈Ư(b)

D. x∉Ư(a) và x∉Ư(b)

Trả lời:

Số x là ước chung của a, b nếu x vừa là ước của a vừa là ước của b.

Đáp án cần chọn là: C

Câu 7. 8 là ước chung của

A. 12 và 32

B. 24 và 56

C. 14 và 48

D. 18 và 24

Trả lời:

24:8 = 3;

56:8 = 7

=> 8 là ước chung của 24 và 56.

Đáp án cần chọn là: B

Câu 8. Tìm ƯCLN(18; 60)

A. 6

B. 30

C. 12

D. 18

Trả lời:

Ta có:

18 = 2.32; 60 = 22.3.5

Nên ƯCLN(18;60) = 2.3 = 6

Đáp án cần chọn là: A

Câu 9. ƯCLN(24, 36) là

A. 36

B. 6

C. 12

D. 24

Trả lời:

Các ước chung của 24 và 36 là 1, 2, 3, 4, 6, 12.

=> ƯC(24, 36) = {1, 2, 3, 4, 6, 12}.

Vì 12 là số lớn nhất trong các ước chung trên nên ƯCLN(24, 36) = 12.

Đáp án cần chọn là: C

Câu 10. Cho ƯCLN(a, b) = 80, ước chung của a và b có thể là:

A. 20

B. 160

C. 30

D. 50

Trả lời:

Ta có 20 là một ước của 80 nên 20 là một ước chung của a và b.

Vậy 20 là số cần tìm.

Đáp án cần chọn là: A

Câu 11. Giao của tập của hai tập hợpA={toán, văn, thể dục, ca nhạc} và

B={mỹ thuật, toán, văn, giáo dục công dân}

A. C={toán, văn, thể dục}

B. C={toán, văn}

C. C={toán, văn, thể dục, ca nhạc}

D. C={toán, thể dục, giáo dục công dân}

Trả lời:

Gọi C=A∩B

Vậy C={toán, văn}

Đáp án cần chọn là: B

Dạng 2. Các dạng toán về ước chung, ước chung lớn nhất

Câu 1. Chọn khẳng định đúng:

A. Mọi số tự nhiên đều có ước chung với nhau.

B. Mọi số tự nhiên đều có ước là 0

C. Số nguyên tố chỉ có đúng 1 ước là chính nó.

D. Hai số nguyên tố khác nhau thì không có ước chung

Trả lời:

A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là 1

B. Đáp án này sai, vì 0 không là ước của 1 số nào cả.

C. Đáp án này sai, vì số nguyên tố có 2 ước là 1 và chính nó.

D. Đáp án này sai, vì 2 số nguyên tố có ước chung là 1.

Đáp án cần chọn là: A

Câu 2. Phân số $\frac{4}{9}$ bằng mấy phân số trong các phân số sau: $\frac{48}{108};\frac{80}{180};\frac{60}{130};\frac{135}{270}?$

A. 1

B. 2

C. 3

D. 4

Trả lời:

ƯCLN(48,108)=12 $\Rightarrow \frac{48}{108}=\frac{4}{9}$

ƯCLN(80,180)=20 $\Rightarrow \frac{80}{180}=\frac{4}{9}$

ƯCLN(60,130)=10 $\Rightarrow \frac{60}{130}=\frac{6}{13}$

ƯCLN(135,270)=135 $\Rightarrow \frac{135}{270}=\frac{1}{2}$

Phân số $\frac{4}{9}$bằng các phân số $\frac{48}{108};\frac{80}{180}$

Vậy có 2 phân số bằng $\frac{4}{9}$

Đáp án cần chọn là: B

Câu 3. Cho a = 32.5.7; b = 24.3.7. Tìm ƯCLN của a và b.

A. ƯCLN(a,b) = 3.7

B. ƯCLN(a,b) = 32.72

C. ƯCLN(a,b) = 24.5

D. ƯCLN(a,b) = 24.32.5.7

Trả lời:

Ta có a=32.5.7;b=24.3.7

a = 32.5.7; b = 24.3.7 nên ƯCLN(a,b) = 3.7

Đáp án cần chọn là: A

Câu 4. Tìm số tự nhiên lớn nhất biết 18⋮x và 32⋮x.

A. 4

B. 2

C. 3

D. 6

Trả lời:

Ta có 18⋮x ⇒ x∈ Ư(18); 32⋮x ⇒ x∈ Ư(32) suy ra x∈ ƯC(18;32)

Mà x lớn nhất nên x = ƯCLN(18;32)

Ta có 18=2.32; 32=25nên ƯCLN(18;32) =2

Hay x = 2.

Đáp án cần chọn là: B

Câu 5. Tìm các ước chung của 18;30;42.

A. {2;3;6}

B. {1;2;3;6}

C. {1;2;3}

D. {1;2;3;6;9}

Trả lời:

+) Ư(18) ={1;2;3;6;9;18}

+) Ư(30) ={1;2;3;5;6;10;15;30}

+) Ư(42) ={1;2;3;6;7;12;14;21;42}

Nên ƯC(18;30;42) ={1;2;3;6}

Đáp án cần chọn là: B

Câu 6. Tìm ước chung của 9 và 15.

A. {1;3}

B. {0;3}

C. {1;5}

D. {1;3;9}

Trả lời:

- Ta có:

Ư(9) ={1,3,9} và Ư(15) ={1,3,5,15}

Vậy ƯC(9,15) = Ư(9)∩ Ư(15) = {1,3}

Đáp án cần chọn là: A

Câu 7. Viết các tập hợp Ư(6); Ư(20); ƯC(6,20).

A. Ư(6) ={1,2,3,6}; Ư(20) ={1,2,4,5,10,20}; ƯC(6,20) ={1,2}

B. Ư(6) ={1,2,3,6}; Ư(20) ={1,2,4,5,20}; ƯC(6,20) ={1,2}

C. Ư(6) ={1,2,3}; Ư(20) ={1,2,4,5,10,20}; ƯC(6,20) ={1,2}

D. Ư(6) ={1,2,4,6}; Ư(20) ={1,2,4,20}; ƯC(6,20) ={1,2,4}

Trả lời:

Ta có:

Ư(6) ={1,2,3,6} và Ư(20) ={1,2,4,5,10,20}

Vậy ƯC(6,20) ={1,2}

Đáp án cần chọn là: A

Câu 8. Giao của tập của hai tập hợpA={toán, văn, thể dục, ca nhạc} và

B={mỹ thuật, toán, văn, giáo dục công dân}}.

A. C = {toán, văn, thể dục}

B. C = {toán, văn}

C. C = {toán, văn, thể dục, ca nhạc}

D. C = {toán, thể dục, giáo dục công dân}

Trả lời:

Gọi C=A∩B

Vậy C={toán, văn}

Đáp án cần chọn là: B

Câu 9. ƯCLN của a và b là:

A. Bằng b nếu a chia hết cho b

B. Bằng a nếu a chia hết cho b

C. Là ước chung nhỏ nhất của a và b

D. Là hiệu của 2 số a và b

Trả lời:

Nếu a chia hết cho b thì b là ước của a.

Mà b cũng là ước của b nên b∈ƯC(a; b)

Hơn nữa bb là ước lớn nhất của b nên ƯCLN(a,b) = b

Đáp án cần chọn là: A

Câu 10. Tìm ƯCLN của 15, 45 và 225.

A. 18

B. 3

C. 15

D. 5

Trả lời:

Ta có: 15 = 3.5; 45 = 32.5;225 = 52.32

Nên ƯCLN(15; 45; 225) = 3.5 = 15.

Đáp án cần chọn là: C

Câu 11. Tìm x biết 120 ⋮ x; 200⋮ x và x < 40

A. x∈{1;2;4;5;8;10;20}

B. x∈{2;5;10;20;40}

C. x∈{1;2;5;10;20;40}

D. x∈{2;5;10;20}

Trả lời:

+) Vì 120⋮x nên x∈Ư(120)={1;2;3;4;5;6;8;10;12;15;20;24;30;40;60;120}

+) Vì 200⋮x nênx∈Ư(200)={1;2;4;5;8;10;20;25;40;50;100;200}

Nên x∈ƯC(120; 200) ={1;2;4;5;8;10;20;40}

mà x < 40 nên x∈{1;2;4;5;8;10;20}

Đáp án cần chọn là: A

Câu 12. Tìm x lớn nhất biết x+220 và x+180 đều chia hết cho x.

A. 15

B. 10

C. 20

D. 18

Trả lời:

Vì x+220 và x+180 đều là bội của xx nên (x+220)⋮x và (x+180)⋮x
Vì x⋮x ⇒ 220⋮xvà 180⋮x
⇒ x∈ ƯC(220;180)
Vì x lớn nhất ⇒ x∈ƯCLN(220;180)

220 = 22.5.11 ; 180 = 22.32.5
⇒ x = ƯCLN(220;180) = 22.5 = 20

Đáp án cần chọn là: C

Câu 13. Một căn phòng hình chữ nhật dài 680cm, rộng480cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch có độ dài lớn nhất là bao nhiêu?

A. 5cm

B. 10cm

C. 20cm

D. 40cm

Trả lời:

Ta có:
Gọi chiều dài viên gạch là x.
Để lát kín căn phòng mà không có có viên gạch nào bị cắt xén thì x phải là ước của chiều dài và chiều rộng căn phòng
Hay 680⋮x và 480⋮x
⇒ x∈ ƯC(680; 480)
Để x là lớn nhất ⇒ x = ƯCLN(680; 480)
Ta có:

680 = 23.5.17;

480 = 25.3.5
⇒ x = ƯCLN(680;480) = 23.5 = 40
Vậy để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì độ dài cạnh viên gạch lớn nhất là 4040 cm.cm.

Đáp án cần chọn là: D

Câu 14. Một khu đất hình chữ nhật có chiều dài 60m, rộng 24m. Người ta chia thành những thửa đất hình vuông bằng nhau, để mỗi thửa đất đó có diện tích lớn nhất thì độ dài cạnh mỗi thửa đất đó là bao nhiêu?

A. 8m

B. 24m

C. 12m

D. 6m

Trả lời:

Gọi cạnh mỗi thửa đất hình vuông chia được là x(m)
Để diện tích các thửa đất đó là lớn nhất thì x phải lớn nhất
Vì các thửa đất đó được chia ra từ đám đất hình chữ nhật ban đầu có chiều dài 60m và 24m
Nên xx phải là ước của 60 và 24
Hay x∈ƯC(6024)
Vì x là lớn nhất nên x= ƯCLN(60;24)
Ta có:

60 = 22.3.5;

24 = 23.3
⇒ x = ƯCLN(60; 24) = 22.3 =12.
Vậy mỗi thửa đất hình vuông đó có độ dài cạnh lớn nhất là 12m.

Đáp án cần chọn là: C

Câu 15. Hoa có 48 viên bi đỏ, 30 viên bi xanh và 60 viên bi vàng. Hoa muốn chia đều số bi vào các túi, sao cho mỗi túi có đủ 3 loại bi. Hỏi Hoa có thể chia vào nhiều nhất bao nhiêu túi mà mỗi túi có số bi mỗi màu bằng nhau.

A. 6

B. 8

C. 4

D.1212

Trả lời:

Ta có:
Gọi số túi mà Hoa chia được là x(túi)
Vì số bi mỗi màu ở mỗi túi cũng bằng nhau nên 48⋮x ; 30⋮x và 60⋮x
⇒x∈ ƯC(48; 30; 60)
Vì x là lớn nhất nên x = ƯCLN(48; 30; 60)
Ta có:

48 = 24.3;

30 = 2.3.5

60 = 22.3.5
⇒x = ƯCLN(48; 30; 60) = 2.3 = 6
Vậy Hoa chia được nhiều nhất là 66 túi mà mỗi túi có số bi mỗi màu bằng nhau.

Đáp án cần chọn là: A

Câu 16. Chọn câu đúng.

A. ƯCLN(44;56)= ƯCLN(48;72)

B. ƯCLN(44;56) < ƯCLN(48;72)

C. ƯCLN(44;56) > ƯCLN(48;72)

D. ƯCLN(44;56) = 1; ƯCLN(48;72) = 3

Trả lời:

Ta có 44 = 22.11; 56 = 23.7 nên ƯCLN (44;56) = 22 = 4.

Lại có48 = 24.3; 72 = 23.32 nên ƯCLN(48;72) = 23.3 = 24.

Nên ƯCLN(44; 56) <ƯCLN(48; 72)

Đáp án cần chọn là: B

Câu 17. Tìm xlớn nhất biết x+160 và x+300 đều là bội của x?

A. 18

B. 20

C. 10

D. 4

Trả lời:

Ta có:
Vì x+160 và x+300 đều là bội của xnên (x+160)⋮x và (x+300)⋮x
Vì x⋮x ⇒160⋮x và 300⋮x
⇒ x∈ ƯC(160;300)
Vì x lớn nhất ⇒ x = ƯCLN(160; 300)
160 = 25.5 và 300 = 22.3.52
⇒ x = ƯCLN(160;300) = 22.5 = 20

Đáp án cần chọn là: B

Câu 18. Một lớp học có 18 nam và 24 nữ được chia đều vào các nhóm sao cho số nam trong các nhóm bằng nhau và số nữ trong các nhóm bằng nhau. Hỏi chia được nhiều nhất bao nhiêu nhóm?

A. 24

B. 18

C. 12

D. 6

Trả lời:

Ta có:
Gọi số nhóm chia được là x (nhóm)
Vì có 18 nam mà số nam ở mỗi nhóm bằng nhau nên 18⋮x
Vì có 24nữ mà số nữ ở mỗi nhóm bằng nhau nên 24⋮x
⇒x∈ƯC(18;24)
Vì xlà lớn nhất nên x= ƯCLN(18;24)

Ta có: 18 = 2.32 ; 24 = 23.3
⇒ x = ƯCLN(18;24) = 2.3 = 6

Vậy chia được nhiều nhất là 6nhóm .

Đáp án cần chọn là: D

Câu 19. Lớp 6A có 40 học sinh, lớp 6B có 48 học sinh, lớp 6C có 32 học sinh. Ba lớp cùng xếp thành hàng như nhau và không lớp nào lẻ hàng. Tính số hàng dọc nhiều nhất mỗi lớp có thể xếp được?

A. 4

B. 12

C. 8

D. 6

Trả lời:

Số hàng dọc nhiều nhất có thể xếp được là ước chung lớn nhất của 40; 48 và 32.

Ta có

40 = 23.5;

48 = 24.3; 32 = 25.

ƯCLN(40; 48; 32) = 23 = 8

Vậy số hàng dọc nhiều nhất mỗi lớp xếp được là 8 hàng.

Đáp án cần chọn là: C

Phần 2. Lý thuyết Ước chung, Ước chung lớn nhất

1. Ước chung

- Một số được gọi là ước chung của hai hay nhiều số nếu nó là ước của tất cả các số đó.

- Tập hợp các ước chung của hai số a và b kí hiệu là ƯC(a, b).

x $\in$ ƯC(a, b) nếu a ⋮ x và b ⋮ x.

- Tương tự, tập hợp các ước chung của a, b, c kí hiệu là ƯC(a, b, c).

x $\in$ ƯC(a, b, c) nếu a ⋮ x, b ⋮ x và c ⋮ x.

Ví dụ:

Ta có: Ư(9) = {1; 3; 9}; Ư(21) = {1; 3; 7; 21}.

Các số 1 và 3 vừa là ước của 9 vừa là ước của 21. Ta nói 1 và 3 là các ước chung của 9 và 21 và viết ƯC(9, 21) = {1; 3}.

Cách tìm ước chung của hai số a và b:

- Viết tập hợp các ước của a và của b: Ư(a), Ư(b).

- Tìm những phần tử chung của Ư(a) và Ư(b).

Ví dụ:

Ư(8) = {1; 2; 4; 8}

Ư(12) = {1; 2; 3; 4; 6; 12}

Do đó ƯC(8; 12) = {1; 2; 4}.

2. Ước chung lớn nhất

Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.

Kí hiệu ước chung lớn nhất của a và b là ƯCLN(a, b).

Tương tự, ước chung lớn nhất của a, b và c là ƯCLN(a, b, c).

Nhận xét: Tất cả các ước chung của hai hay nhiều số đều là ước của ƯCLN của các số đó.

Ví dụ:

ƯC(16, 24) = {1; 2; 4; 8} nên ƯCLN(16, 24) = 8, vì 8 là số lớn nhất trong số các ước chung của 16 và 24. Các ước chung của 36 và 45 là 1; 2; 4; 8 đều là ước của 8.

Nhận xét: Với mọi số tự nhiên a và b, ta có:

ƯCLN(a, 1) = 1; ƯCLN(a, b, 1) = 1.

Ví dụ: ƯCLN(9, 1) = 1; ƯCLN(5, 18, 1) = 1.

3. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố

Quy tắc:

Muốn tìm ƯCLN của của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.

Ví dụ: Tìm ƯCLN (36; 60).

Hướng dẫn giải

Bước 1: Phân tích các số ra thừa số nguyên tố.

36 = 22 . 32

60 = 22 . 3 . 5

Bước 2: Thừa số nguyên tố chung là 2 và 3.

Bước 3: Số mũ nhỏ nhất của thừa số 2 là 2 và của 3 là 1.

ƯCLN(18; 30) = 22 . 3 = 12.

Chú ý: Hai số có ƯCLN bằng 1 gọi là hai số nguyên tố cùng nhau.

Ví dụ: ƯCLN(15; 23) = 1 nên 15 và 23 được gọi là hai số nguyên tố cùng nhau.

4. Ứng dụng trong rút gọn về số tối giản

Rút gọn phân số: Chia cả tử và mẫu cho ước chung khác 1 (nếu có) của chúng.

Phân số tối giản: ab là phân số tối giản nếu ƯCLN(a, b) = 1.

Đưa một phân số chưa tối giản về phân số tối giản:

Chia cả tử và mẫu cho ƯCLN(a, b).

Ví dụ: Phân số $\text{Unexpected text node: '9/24 là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản.'}$

Hướng dẫn giải

Vì ƯCLN(9, 24) = 3 ≠ 1 nên 9/24 chưa phải là phân số tối giản.

Ta có:  

Khi đó, ta được 3/8 là phân số tối giản.