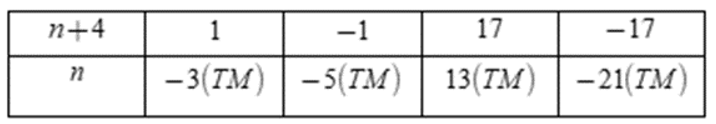30 câu Trắc nghiệm Phân số với tử số và mẫu số là số nguyên (có đáp án 2024) – Toán 6 Chân trời sáng tạo

Trắc nghiệm Toán lớp 6 Bài 1: Phân số với tử số và mẫu số là số nguyên

Phần 1. Trắc nghiệm Phân số với tử số và mẫu số là số nguyên

Dạng 1. Phân số với tử số và mẫu số là số nguyên

Câu 1. Tính tổng các giá trị biết rằng $-\frac{111}{37}<x<\frac{91}{13}$

A. 22

B. 20

C. 18

D. 15

Trả lời:

Ta có:

$-\frac{111}{37}<x<\frac{91}{13}$

⇒ −3 < x < 7

⇒ x∈{−2; −1; 0; 1; 2; 3; 4; 5; 6}

Vậy tổng các giá trị của x thỏa mãn là: (−2) + (−1) +...+ 5 + 6 = 18

Đáp án cần chọn là: C

Câu 2. Điền số thích hợp vào chỗ chấm $\frac{15}{90}=\frac{5}{\mathrm{...}}$

A. 20

B. – 60

C. 60

D. 30

Trả lời:

$$\begin{gathered} \frac{15}{90}=\frac{5}{x} \\ 15x=90.5 \\ x=\frac{90.5}{15}=30 \end{gathered}$$

Vậy số cần điền là: 30.

Đáp án cần chọn là: D

Câu 3. Viết 20 dm2 dưới dạng phân số với đơn vị là mét vuông

A.$\frac{100}{20}\left(m^2\right)$

B.$\frac{20}{100}\left(m^2\right)$

C.$\frac{20}{10}\left(m^2\right)$

D.$\frac{20}{1000}\left(m^2\right)$

Trả lời:

Ta có:$20d{m}^2=\frac{20}{100}\left(m^2\right)$

Đáp án cần chọn là: B

Câu 4. Nhận xét nào sau đây là đúng khi nói về phân số?

A. Phân số nhỏ hơn số 0 gọi là phân số âm.

B. Phân số lớn hơn số 0 gọi là phân số dương.

C. Phân số âm nhỏ hơn phân số dương.

D. Cả A, B và C đều đúng.

Trả lời:

Những nhận xét đúng là:

- Phân số nhỏ hơn số 0 gọi là phân số âm.

- Phân số lớn hơn số 0 gọi là phân số dương.

- Phân số âm nhỏ hơn phân số dương.

Đáp án cần chọn là: D

Câu 5. Viết số nguyên a dưới dạng phân số ta được:

A.$\frac{a}{0}$

B.$\frac{0}{a}$

C.$\frac{a}{1}$

D.$\frac{1}{a}$

Trả lời:

Viết số nguyên aa dưới dạng phân số ta được: $\frac{a}{1}$

Đáp án cần chọn là: C

Câu 6. Viết phân số âm năm phần tám

A.$\frac{5}{8}$

B.$\frac{8}{-5}$

C.$\frac{-5}{8}$

D.– 5,8

Trả lời:

Phân số âm năm phần tám được viết là $\frac{-5}{8}$

Đáp án cần chọn là: C

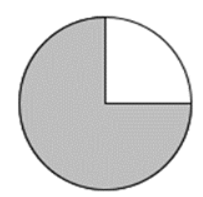
Câu 7. Phần tô màu trong hình sau biểu diễn phân số nào?

A.$\frac{1}{2}$

B.$\frac{1}{4}$

C.$\frac{3}{4}$

D.$\frac{5}{8}$

Trả lời:

Quan sát hình vẽ ta thấy nếu chia hình tròn làm 4phần thì phần tô màu chiếm 3 phần.

Vậy phân số biểu diễnphần tô màu là $\frac{3}{4}$

Đáp án cần chọn là: C

Câu 8. Hãy viết phép chia sau dưới dạng phân số: (-58) : 73

A.$\frac{-58}{73}$

B.$\frac{58}{73}$

C.$\frac{73}{-58}$

D.$\frac{58}{73}$

Trả lời:

Phép chia (-58) : 73 được viết dưới dạng phân số là:$\frac{-58}{73}$

Đáp án cần chọn là: A

Câu 9. Phân số nào dưới đây bằng với phân số $\frac{-2}{5}$

A.$\frac{4}{10}$

B.$\frac{-6}{15}$

C.$\frac{6}{15}$

D.$\frac{-4}{-10}$

Trả lời:

Đáp án A:

Vì −2.10 ≠ 4.5 nên$\frac{-2}{5}\ne \frac{4}{10}$

⇒ A sai.

Đáp án B:

Vì (−2).15 = (−6).5 = −30 nên $\frac{-2}{5}=\frac{-6}{15}$

⇒ B đúng.

Đáp án C:

(−2).15 ≠ 6.5 nên $\frac{-2}{5}\ne \frac{6}{15}$

⇒ C sai.

Đáp án D:

Vì (−2).(−10) ≠ (−4).5 nên $\frac{-2}{5}\frac{-4}{-10}$

⇒ D sai.

Đáp án cần chọn là: B

Câu 10. Chọn câu sai?

A.$\frac{1}{3}=\frac{45}{135}$

B.$\frac{-13}{20}=\frac{26}{-40}$

C.$\frac{-4}{15}=\frac{-16}{-60}$

D.$\frac{6}{7}=\frac{-42}{-49}$

Trả lời:

Đáp án A:

Vì 1.135 = 3.45 nên $\frac{1}{3}=\frac{45}{135}$

⇒A đúng.

Đáp án B:

Vì (−13).(−40)=20.26 nên $\frac{-13}{20}=\frac{26}{-40}$

⇒B đúng.

Đáp án C:

Vì (−4).(−60)≠15.(−16) nên $\frac{-4}{15}=\frac{-16}{-60}$

⇒C sai.

Đáp án D:

Vì 6.(−49)=7.(−42) nên $\frac{6}{7}=\frac{-42}{-49}$

⇒D đúng.

Đáp án cần chọn là: C

Câu 11. Cách viết nào sau đây cho ta một phân số:

A.$\frac{4}{0}$

B.$\frac{\mathrm{1,5}}{3}$

C.$\frac{0}{7}$

D.$\frac{-5}{\mathrm{3,5}}$

Trả lời:

+ $\frac{4}{0}$ có mẫu bằng 0 nên không là phân số

+$\frac{\mathrm{1,5}}{3}$ có 1,5∉Z nên không là phân số

+ $\frac{0}{7}$ là phân số

+ $\frac{-5}{\mathrm{3,5}}$ có 3,5∉Z nên không là phân số

Đáp án cần chọn là: C

Câu 12. Phân số có tử bằng – 4, mẫu bằng 5 được viết là:

A.$\frac{-5}{4}$

B.$\frac{4}{5}$

C.$\frac{-4}{5}$

D.$\frac{5}{4}$

Trả lời:

Phân số có tử bằng −4, mẫu bằng 5 được viết là: $\frac{-4}{5}$

Đáp án cần chọn là: C

Dạng 2. Các dạng toán về phân số với tử số và mẫu số là số nguyên

Câu 1. Có bao nhiêu giá trị nguyên dương của n để $\frac{9}{4n+1}$ đạt giá trị nguyên.

A. 1

B. 0

C. 2

D. 3

Trả lời:

Vì n nguyên dương nên để $\frac{9}{4n+1}$ nguyên thì 4n+1∈U(9) = {±1; ±3; ±9}

Ta có bảng:

Vậy có duy nhất một giá trị của n thỏa mãn là n = 2

Đáp án cần chọn là: A

Câu 2. Tổng các số a, b, c thỏa mãn $\frac{6}{9}=\frac{12}{a}=\frac{b}{-54}=\frac{-738}{c}$ là:

A. 1161

B. – 1125

C. – 1053

D. 1089

Trả lời:

Ta có:

$$\begin{gathered} \frac{6}{9}=\frac{12}{a}\Rightarrow 6.a=9.12\Rightarrow a=\frac{9.12}{6}=18 \\ \frac{6}{9}=\frac{b}{-54}\Rightarrow 6.\left(-54\right)=9.b\Rightarrow b=\frac{6.\left(-54\right)}{9}=-36 \\ \frac{6}{9}=\frac{-738}{c}\Rightarrow 6.c=9.\left(-738\right)\Rightarrow c=\frac{9.\left(-738\right)}{6}=-1107 \end{gathered}$$

Vậy a + b + c = 18 + (-36) + (-1107) = - 1125

Đáp án cần chọn là: B

Câu 3. Cho các phân số:$\frac{15}{60};\frac{-7}{5};\frac{6}{15};\frac{28}{-20};\frac{3}{12}$ . Số cặp phân số bằng nhau trong những phân số trên là:

A. 4

B. 1

C. 3

D. 2

Trả lời:

- Các phân số dương: $\frac{15}{60};\frac{6}{15};\frac{3}{12}$

+ Vì 15.15 ≠ 60.6 nên $\frac{15}{60}\ne \frac{6}{15}$

+ Vì 6.12 ≠ 15.3 nên $\frac{6}{15}\ne \frac{3}{12}$

+ Vì 15.12 = 60.3 nên $\frac{15}{60}=\frac{3}{12}$

- Các phân số âm: $\frac{-7}{5};\frac{28}{-20}$

Vì (−7).(−20) = 5.28 nên $\frac{-7}{5};\frac{28}{-20}$

Vậy có hai cặp phân số bằng nhau trong các phân số đã cho.

Đáp án cần chọn là: D

Câu 4. Tìm tập hợp các số nguyên n để $A=\frac{3n-5}{n+4}$ có giá trị là số nguyên.

A. n∈{13}

B. n∈{−21; −5; −3; 13}

C. n∈{−17; −1; 1; 17}

D. n∈{−13; −3; 3; 13}

Trả lời:

Ta có:

$$\begin{gathered} A=\frac{3n-5}{n+4}=\frac{3n+12-12-5}{n+4} \\ =\frac{3\left(n+4\right)+\left(-17\right)}{n+4} \\ =\frac{3\left(n+4\right)}{n+4}+\frac{-17}{n+4} \\ =3+\frac{-17}{n+4} \end{gathered}$$

Vì n∈Z nên để A∈Z thì n+4∈U(−17) = {±1; ±17}

Ta có bảng:

Vậy n∈{−21; −5; −3; 13}

Đáp án cần chọn là: B

Câu 5. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn $\frac{x}{5}=\frac{3}{y}$ và x > y?

A. 4

B. 3

C. 2

D. 1

Trả lời:

Ta có:

$\frac{x}{5}=\frac{3}{y}$ ⇒ x.y = 5.3 = 15

Mà 15 = 5.3 = 15.1 = (−3).(−5) = (−1).(−15)

và x,y ∈ Z, x > y nên (x;y) ∈ {(5;3), (15;1), (−3;−5), (−1;−15)}

Đáp án cần chọn là: A

Câu 6. Trong các cách viết sau đây, cách viết nào cho ta phân số:

A.$\frac{12}{0}$

B.$\frac{-4}{5}$

C.$\frac{3}{\mathrm{0,25}}$

D.$\frac{\mathrm{4,4}}{\mathrm{11,5}}$

Trả lời:

+) $\frac{12}{0}$không là phân số vì mẫu số bằng 0.

+)$\frac{3}{\mathrm{0,25}}$ không là phân số vì mẫu số là số thập phân.

+) $\frac{\mathrm{4,4}}{\mathrm{11,5}}$không là phân số vì tử số và mẫu số là số thập phân.

+) $\frac{-4}{5}$ là phân số vì −4; 5∈Z và mẫu số là 5 khác 0.

Đáp án cần chọn là: B

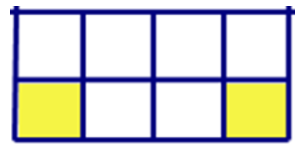
Câu 7. Phần tô màu trong hình sau biểu diễn phân số nào?

A.$\frac{1}{2}$

B.$\frac{1}{4}$

C.$\frac{3}{4}$

D.$\frac{5}{8}$

Trả lời:

Trong hình có 2 ô vuông tô màu và tổng tất cả 8 ô vuông nên phân số biểu thị là$\frac{2}{8}=\frac{1}{4}$

Đáp án cần chọn là: B

Câu 8. Tìm số nguyên x biết $\frac{35}{15}=\frac{x}{3}$ ?

A. x = 7

B. x = 5

C. x = 15

D. x = 6

Trả lời:

$\frac{35}{15}=\frac{x}{3}$

35 . 3 = 15 . x

$x=\frac{35.3}{15}$

x = 7

Vậy x = 7

Đáp án cần chọn là: A

Câu 9. Cho tập A = {1; −2; 3; 4}. Có bao nhiêu phân số có tử số và mẫu số thuộc A mà có tử số khác mẫu số và tử số trái dấu với mẫu số?

A. 9

B. 6

C. 3

D. 12

Trả lời:

Các phân số thỏa mãn bài toán là:

$\frac{1}{-2};\frac{3}{-2};\frac{4}{-2};\frac{-2}{1};\frac{-2}{3};\frac{-2}{4}$

Vậy có tất cả 6 phân số.

Đáp án cần chọn là: B

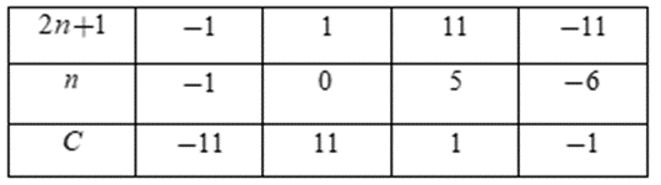
Câu 10. Cho biểu thức $C=\frac{11}{2n+1}$. Tìm tất cả các giá trị của n nguyên để giá trị của C là một số tự nhiên.

A. n∈{−6; −1; 0; 5}

B. n∈{−1; 5}

C. n∈{0; 5}

D. n∈{1; 11}

Trả lời:

Vì C∈N nên C∈Z. Do đó ta tìm n∈Z để C∈Z

Vì n∈Z nên để C∈Z thì 2n+1∈U(11) = {±1; ±11}

Ta có bảng:

Vì C∈N nên ta chỉ nhận các giá trị n = 0; n = 5

Đáp án cần chọn là: C

Câu 11. Tìm x; y biết $\frac{x-4}{y-3}=\frac{4}{3}$ và x – y = 5.

A. x = 15; y = 5

B. x = 5; y = 15

C. x = 20; y = 15

D. x = 25; y = 10

Trả lời:

Ta có: x – y = 5 ⇒ x = y + 5 thay vào $\frac{x-4}{y-3}=\frac{4}{3}$ ta được:

$\frac{y+5-4}{y-3}=\frac{4}{3}$

$\frac{y+1}{y-3}=\frac{4}{3}$

3(y + 1) = 4(y − 3)

3y + 3 = 4y − 12

3y − 4y = −12 − 3

−y = −15

y = 15

⇒ x = 15 + 5 = 20

Vậy x = 20; y = 15

Đáp án cần chọn là: C

Câu 12. Tìm số nguyên x biết rằng $\frac{x}{3}=\frac{27}{x}$ và x < 0.

A. x = 81

B. x = −81

C. x = −9

D. x = 9

Trả lời:

$\frac{x}{3}=\frac{27}{x}$

x.x = 81

x2 = 81

Ta có: x = 9 hoặc x = −9

Kết hợp điều kiện x < 0 nên có một giá trị x thỏa mãn là: x = −9

Đáp án cần chọn là: C

Câu 13. Viết số nguyên – 16 dưới dạng phân số ta được:

A.$\frac{-16}{0}$

B.$\frac{16}{1}$

C.$\frac{-16}{1}$

D.$\frac{16}{0}$

Trả lời:

Viết số nguyên −16 dưới dạng phân số ta được: $\frac{-16}{1}$

Đáp án cần chọn là: C

Câu 14. Phân số $\frac{-9}{7}$ được đọc là:

A. Chín phần bảy

B. Âm bảy phần chín

C. Bảy phần chín

D. Âm chín phần bảy

Trả lời:

Phân số $\frac{-9}{7}$ được đọc là: Âm chín phần bảy

Đáp án cần chọn là: D

Phần 2. Lý thuyết  Phân số với tử số và mẫu số là số nguyên

1. Khái niệm phân số

Ta gọi 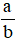, trong đó  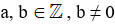là phân số, a là tử số (tử), b là mẫu số (mẫu) của phân số. Phân số  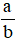đọc là a phần b.

Ví dụ 1. Phân số 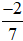 có tử số là −2, mẫu số là 7 và được đọc là “âm hai phần bảy”.

Chú ý: Ta có thể dùng phân số để ghi (viết, biểu diễn) kết quả phép chia một số nguyên cho một số nguyên khác 0.

Ví dụ 2. Phân số 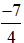 là ghi kết quả phép chia −7 cho 4.

2. Phân số bằng nhau
 Hai phân số 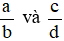 được gọi là bằng nhau, viết là 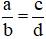, nếu a . d = b . c.

Ví dụ 3. 

a) 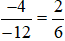 vì (−4) . 6 = (−12) . 2 (cùng bằng –24).

b)  không bằng 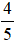, vì 3 . 5 không bằng 4 . 4. Viết .

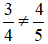Chú ý: Điều kiện a . d = b . c gọi là điều kiện bằng nhau của hai phân số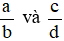  

Ví dụ 4. Các cặp phân số sau có bằng nhau hay không?

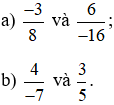
Lời giải:

a)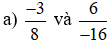 

So sánh hai tích: (−3) . (−16) và 8 . 6;

Ta có: (−3) . (−16) = 3 . 16 = 48 và 8 . 6 = 48.

Nên (−3) . (−16) = 8 . 6. Do đó .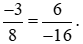

.

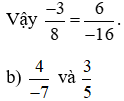So sánh hai tích: 4 . 5 và (−7) . 3;

Ta có: 4 . 5 = 20 và (−7) . 3 = −21.

Nên 4 . 5 ≠ (−7) . 3. Do đó .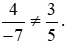

Vậy hai phân số 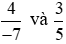 không bằng nhau.

3. Biểu diễn số nguyên ở dạng phân số 

Mỗi số nguyên n có thể coi là phân số 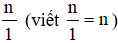. Khi đó số nguyên n được biểu diễn ở dạng phân số .

Ví dụ 5. 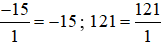.