50 câu Trắc nghiệm Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây (có đáp án 2024) – Toán 10 Cánh diều

Đáp án đúng là: B

Gọi số tự nhiên có 4 chữ số cần tìm là: $\overline{abcd}$ (a ≠ 0), khi đó:

a có 4 cách chọn (vì a có thể chọn tuỳ ý một trong 4 số 5; 6; 7; 8)

b có 4 cách chọn (vì b ≠ a nên b không được chọn lại số mà a đã chọn vậy b có 4 số để chọn)

c có 3 cách chọn (vì c ≠ a, c ≠ b nên c không được chọn lại số mà a, b đã chọn vậy c còn 3 số để chọn)

d có 2 cách chọn (vì d ≠ a, d ≠ b, d ≠ c nên d không được chọn lại số mà a, b, c đã chọn vậy c còn 2 số để chọn)

Vậy có: 4.4.3.2 = 96 số

Đáp án đúng là: A

Gọi số tự nhiên chẵn có 4 chữ số cần tìm là: $\overline{abcd}$ (a ≠ 0) khi đó:

d có 3 cách chọn (vì số tự nhiên chẵn nên d có thể chọn một trong 3 số 2; 4; 6)

a có 5 cách chọn (vì a có thể chọn tuỳ ý một trong 5 số 2; 3; 4; 5; 6)

b có 5 cách chọn (vì b có thể chọn tuỳ ý một trong 5 số 2; 3; 4; 5; 6)

c có 5 cách chọn (vì c có thể chọn tuỳ ý một trong 5 số 2; 3; 4; 5; 6)

Vậy có: 3.5.5.5 = 375 số

Đáp án đúng là: C

Gọi số có ba chữ số cần tìm là $\overline{abcd}$, với a ≠ 0

a có 6 cách chọn (vì a ≠ 0 nên a có thể chọn một trong 6 số 1; 2; 3; 4; 5; 6)

b có 7 cách chọn (vì b có thể chọn tuỳ ý một trong 7 số 0; 1; 2; 3; 4; 5; 6)

c có 7 cách chọn (vì c có thể chọn tuỳ ý một trong 7 số 0; 1; 2; 3; 4; 5; 6)

d có 4 cách chọn (vì $\overline{abcd}$ là số chẵn nên d phải là số chẵn vậy d chỉ được chọn một trong 4 số 0; 2; 4; 6)

Vậy số các số cần tìm là 6.7.7.4 = 1176 (số)

Đáp án đúng là: B

Gọi số tự nhiên có ba chữ số khác nhau là $\overline{abc}$ (a ≠ 0). Do số cần lập là số chẵn và phải có mặt chữ số 2 nên ta có các trường hợp.

Trường hợp 1: a = 2 khi đó số có dạng $\overline{2bc}$.

Chọn c có 2 cách (vì c ≠ 2 và $\overline{abc}$ là số chẵn nên c chọn được một trong các số 0; 8)

Chọn b có 4 cách (vì b ≠ 2 và b ≠ c nên b được chọn một trong các số 0; 1; 3; 5; 8 nhưng bỏ đi số mà c đã chọn)

Theo quy tắc nhân có 4.2 = 8 số.

Trường hợp 2: b = 2 và c = 0 khi đó số có dạng $\overline{a20}$.

Chọn a có 4 cách (vì a ≠ 2, a ≠ 0 nên a được chọn một trong các số 1; 3; 5; 8)

Theo quy tắc nhân có 1.1.4 = 4 số.

Trường hợp 3: b = 2 và c = 8 khi đó số có dạng $\overline{a28}$.

Chọn a có 3 cách (vì a ≠ 2 và a ≠ 0 nên a được chọn một trong các số 1; 3; 5)

Theo quy tắc nhân có 1.1.3 = 3 số.

Trường hợp 4: c = 2 khi đó số có dạng $\overline{ab2}$.

Chọn a có 4 cách (vì a ≠ 2 và a ≠ 0 nên a chọn được một trong các số 1; 3; 5; 8)

Chọn b có 4 cách (vì b ≠ 2 và b ≠ a nên b được chọn một trong các số 0; 1; 3; 5; 8 nhưng bỏ đi số mà a đã chọn)

Theo quy tắc nhân có 1.4.4 = 16 số.

Theo quy tắc cộng có 8 + 4 + 3 + 6 = 21 (số).

Đáp án đúng là: D

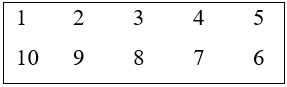
Ta đánh số liên tiếp 12 chỗ ngồi bằng các số từ 1 đến 6 thuộc một dãy và từ 7 đến 12 thuộc một dãy như sau:

Để xếp vị trí ta có các cách chọn như sau:

Vậy có: 460800 cách xếp.

Đáp án đúng là: C

Gọi số tự nhiên có 3 chữ số cần tìm là: $\overline{abc}$ (a ≠ 0) khi đó:

c có 3 cách chọn (vì $\overline{abc}$ là số lẻ nên c có thể chọn 1 trong 3 số 3; 5; 7)

a có 6 cách chọn (vì a có thể chọn tuỳ ý một trong 6 số 2; 3; 4; 5; 6; 7)

b có 7 cách chọn (vì b có thể chọn tuỳ ý một trong 7 số 0; 2; 3; 4; 5; 6; 7)

Vậy có: 3.6.7 = 126 số

Đáp án đúng là: D

Gọi số tự nhiên cần tìm có dạng $\overline{abc}$ (a ≠ 0) Khi đó:

a có 4 cách chọn (vì a là số chẵn và a ≠ 0 nên a chỉ được chọn một trong 4 số 2; 4; 6; 8)

b có 5 cách chọn (vì b là số chẵn nên b chỉ được chọn một trong 5 số 0; 2; 4; 6; 8)

c có 5 cách chọn (vì c là số chẵn nên c chỉ được chọn một trong 5 số 0; 2; 4; 6; 8)

Vậy ta có: 4.5.5 = 100 số

Đáp án đúng là: A

Gọi số có bốn chữ số cần tìm là $\overline{abcd}$, với a ≠ 0

Chọn số d có 3 cách chọn (vì số $\overline{abcd}$ là số lẻ nên d có thể chọn một trong 3 số là 1; 3; 5)

Chọn số a có 6 cách chọn (vì a ≠ 0 nên a có thể chọn một trong 6 số là 1; 2; 3; 4; 5; 6)

Chọn số b có 7 cách chọn(vì b chọn tuỳ ý nên b có thể chọn một trong 7 số là 0; 1; 2; 3; 4; 5; 6)

Chọn số c có 7 cách chọn(vì c chọn tuỳ ý nên c có thể chọn một trong 7 số là 0; 1; 2; 3; 4; 5; 6)

Số các số tự nhiên lẻ có 4 chữ số lập từ các số trên là: 3.6.7.7 = 882 (số)

Đáp án đúng là: B

Việc chọn hai địa điểm ở Quy Nhơn và Đà Nẵng để tham quan là thực hiện hai hành động liên tiếp: Chọn một địa điểm ở Quy Nhơn, sau đó chọn một địa điểm ở Đà Nẵng.

Có 5 cách chọn địa điểm thao quan ở Quy Nhơn.

Với mỗi cách chọn một địa điểm tham quan ở Quy Nhơn, có 7 cách chọn địa điểm tham quan ở Đà Nẵng.

Vậy gia đình bạn Dương có tất cả 5.7 =35 cách chọn.