50 câu Trắc nghiệm Ôn tập Chương 1 (có đáp án 2024) – Toán 10 Cánh diều

Trắc nghiệm Toán 10 Ôn tập Chương 1

Câu 1. Cho các mệnh đề sau, mệnh đề nào sai:

A. Một tam giác vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại.  

B. Một tam giác đều thì có hai trung tuyến bằng nhau và một góc bằng 600.       

C. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một cạnh bằng nhau.

D. Một tứ giác là hình chữ nhật thì nó có 3 góc vuông.

Câu 2. Một nhóm các học sinh lớp 10H giỏi Toán hoặc giỏi Văn. Trong đó, có 5 bạn giỏi Toán; 7 bạn giỏi Văn và 2 bạn giỏi cả hai môn. Hỏi nhóm đó có bao nhiêu học sinh?

A. 14;

B. 10;                                 

C. 12;                                 

D. 7.

Câu 3. Kí hiệu nào sau đây để chỉ $\sqrt{5}$ không phải là số hữu tỉ?

A. $\sqrt{5}\ne \mathbb{Q}$;

B. $\sqrt{5}\not\subset \mathbb{Q}$;

C. $\sqrt{5}\notin \mathbb{Q}$;

D. $\sqrt{5}\in \mathbb{Q}$.

Câu 4. Một lớp có 45 học sinh. Mỗi em đều đăng ký chơi ít nhất một trong hai môn: bóng đá và bóng chuyền. Có 35 em đăng ký môn bóng đá, 15 em đăng ký môn bóng chuyền. Hỏi có bao nhiêu em đăng ký cả hai môn bóng đá và bóng chuyền?

A. 30;                                 

B. 10;                                 

C. 5;

D. 25.

Câu 5. Cho hai tập hợp A = [−1; 3), B = [a; a + 3]. Với giá trị nào của a thì A ∩ B = ∅?

A. $\left[\begin{array}{l}a\ge 3\\ a\le -4\end{array}\right.$;

B. $\left[\begin{array}{l}a>3\\ a<-4\end{array}\right.$;

C. $\left[\begin{array}{l}a\ge 3\\ a<-4\end{array}\right.$;

D. $\left[\begin{array}{l}a>3\\ a\le -4\end{array}\right.$;

Câu 6. Cho tập A = (−∞; 1] và B = (m; +∞). Tất cả các giá trị của m để A ∩ B ≠ ∅ là:

A. m > 1;                           

B. m ≤ 1;                            

C. m < 1;                           

D. m ≥ 1.

Câu 7. Cho hai tập A, B khác rỗng. Câu nào sau đây đúng

A. Nếu A ∩ B = A thì  A ⊂ B;                               

B. A ∪ B = A khi và chỉ khi B ⊂ A;                      

C. A \ B = A khi và chỉ khi A ∩ B = ∅ ;

D. Cả ba câu trên đều đúng.

Câu 8. Xác định tập hợp A = {x ∈ $\mathbb{N}$| x2 − 2x – 3 = 0} bằng cách liệt kê các phần tử

A. A = {−1;3};                   

B. A = {1; −3};                  

C. A = {1};                        

D. A = {3}.

Câu 9. Trong các mệnh đề sau, tìm mệnh đề đúng?

A. “∃ x ∈ $ℝ$: x2 < 0”;        

B. “∃ x ∈ $ℝ$: x2 + x + 3 = 0”;                                

C. “∀ x ∈ $ℝ$: x2 > x”;

D. “∃ x ∈ $\mathbb{Z}$: x > −x”.

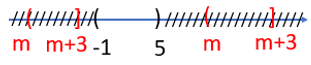
Câu 10. Cho A = (−1; 5) và B = (m; m+3]. Tìm tất cả các giá trị của m để A ∩ B ≠ ∅ ?

A. m ≤ −4;                         

B. m > 5;                            

C. −4 < m < 5;                   

D. −4 ≤ m < 5.

Câu 11. Cho A = (−20; 20) và B = [2m – 4; 2m + 2) (m là tham số). Có tất cả bao nhiêu giá trị nguyên dương của tham số m để B ⊂ A?

A. 9;                                  

B. 17;                                 

C. 8;

D. 10.