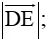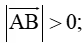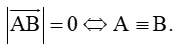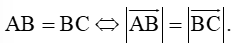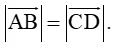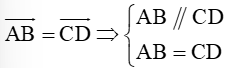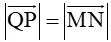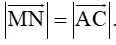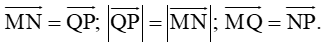50 câu Trắc nghiệm Khái niệm vectơ (có đáp án 2024) – Toán 10 Cánh diều
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Bài 3: Khái niệm vectơ đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 3.
Trắc nghiệm Toán 10 Bài 3: Khái niệm vectơ
Câu 1. Hai vectơ được gọi là bằng nhau khi và chỉ khi
A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau.
B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành.
C. Chúng trùng với một trong các cặp cạnh đối của một tam giác đều.
D. Chúng cùng hướng và độ dài của chúng bằng nhau.
Đáp án đúng là : D
Theo định nghĩa hai vectơ bằng nhau: Hai vectơ →a và →b được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu →a= →b.
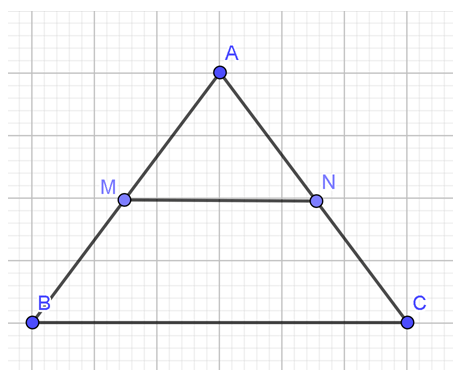
Câu 2. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC của tam giác đều ABC. Hỏi cặp vectơ nào sau đây cùng hướng?
A. →MN và →CB.
B. →AB và →MB.
C. →MA và →MB.
D. →AN và →CA.
Đáp án đúng là: B
Quan sát ta thấy: →AB và →MB cùng hướng.
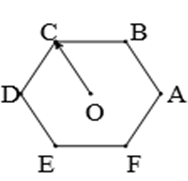
Câu 3. Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ - không, cùng phương với →OC có điểm đầu và điểm cuối là các đỉnh của lục giác là
A. 4;
B. 6;
C. 7;
D. 9.
Đáp án đúng là: B
Đó là các vectơ: →AB,→BA,→DE,→ED,→FC,→CF.
Câu 4. Vectơ có điểm đầu là D, điểm cuối là E được kí hiệu là
A. DE;
B.
C. →ED;
D. →DE.
Đáp án đúng là: D
Theo định nghĩa vectơ: Vectơ có điểm đầu A, điểm cuối B được kí hiệu là →AB và đọc là 'vectơ AB'. Để vẽ vectơ →AB ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu mút B.
Do đó, với điểm đầu là D và điểm cuối là E ta có vecto →DE.
Câu 5. Cho tam giác ABC, có bao nhiêu vectơ khác vectơ - không, có điểm đầu và điểm cuối là các đỉnh A, B, C.
A. 3
B. 6
C. 4
D. 9
Đáp án đúng là: B
Đó là các vectơ: →AB,→BA,→BC,→CB,→CA,→AC.
Câu 6. Cho tứ giác ABCD,có bao nhiêu vectơ khác vectơ - không, có điểm đầu và cuối là các đỉnh của tứ giác?
A. 4
B. 6
C. 8
D. 12
Đáp án đúng là: D
Xét các vectơ có điểm A là điểm đầu thì có các vectơ thỏa mãn bài toán là →AB,→AC,→AD⇒ có 3 vectơ.
Tương tự cho các điểm còn lại B, C, D. Như vậy sẽ có tất cả 12 vectơ.
Câu 7. Với →DE (khác vectơ - không) thì độ dài đoạn thẳng ED được gọi là
A. Phương của →ED;
B. Hướng của →ED;
C. Giá của →ED;
D. Độ dài của →ED;
Đáp án đúng là : D
Theo định nghĩa độ dài vectơ : Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của nó hay nói gọn hơn, độ dài của vectơ →ABlà độ dài đoạn thẳng AB, kí hiệu là 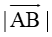
Do đó, độ dài đoạn thẳng ED là độ dài vecto →ED.
Câu 8. Mệnh đề nào sau đây sai?
A. →AA=→0;
B. →0 cùng hướng với mọi vectơ.
C.
D. →0 cùng phương với mọi vectơ.
Đáp án đúng là : C
Vì có thể xảy ra trường hợp
Câu 9. Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Đáp án đúng là: A
Vì vectơ - không, cùng phương với mọi vectơ.
Câu 10. Cho ba điểm A, B, C phân biệt. Khi đó:
A. Điều kiện cần và đủ để A, B, C thẳng hàng là →AB cùng phương với →AC.
B. Điều kiện đủ để A, B, C thẳng hàng là với mọi M,→MAcùng phương với →AB.
C. Điều kiện cần để A, B, C thẳng hàng là với mọi M, →MAcùng phương với →AB.
D. Điều kiện cần để A, B, C thẳng hàng là →AB=→AC.
Đáp án đúng là: A
Điều kiện cần và đủ để A, B, C thẳng hàng là →AB cùng phương với →AC.
Câu 11. Cho bốn điểm phân biệt A, B, C, D. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để →AB=→CD?
A. ABCD là hình bình hành.
B. ABCD là hình tứ giác
C. AC = BD
D. AB = CD
Đáp án đúng là : A
Ta có:
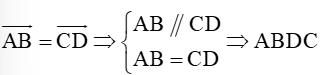
Mặt khác, ABCD là hình bình hành 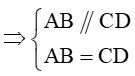
Do đó, điều kiện cần và đủ để →AB=→CD là ABCD là hình bình hành.
Câu 12. Cho hình vuông ABCD. Khẳng định nào sau đây đúng?
A. →AC=→BD;
B. →AB=→CD;
C.
D. Hai vectơ →AB,→AC cùng hướng.
Đáp án đúng là: C
Vì
Câu 13. Cho bốn điểm phân biệt A, B, C, D thỏa mãn →AB=→CD. Khẳng định nào sau đây sai?
A. →AB cùng hướng →CD.
B. →AB cùng phương →CD.
C.
D. ABCD là hình bình hành.
Đáp án đúng là : D
Ta có :
→AB;→CD cùng hướng.
⇒ABDC là hình bình hành
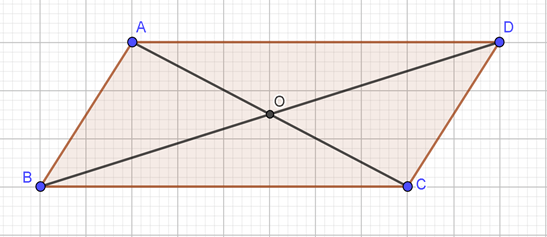
Câu 14. Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. →AB=→DC;
B. →OB=→DO;
C. →OA=→OC;
D. →CB=→DA.
Đáp án đúng là: C
Quan sát hình vẽ ta thấy: →AB=→DC;→OB=→DO;→CB=→DA.
Do đó, C sai
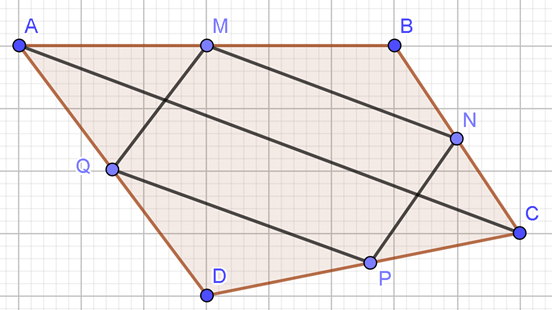
Câu 15. Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB,BC,CD,DA. Khẳng định nào sau đây sai?
A. →MN=→QP;
B.
C. →MQ=→NP;
D.
Đáp án đúng là: D
Ta có: 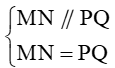
Do đó MNPQ là hình bình hành.
Vì MNPQ là hình bình hành nên