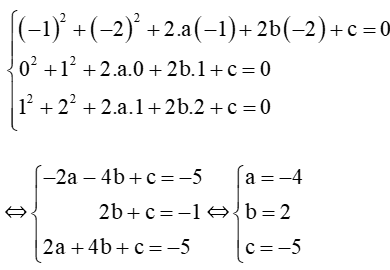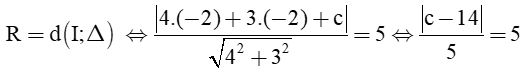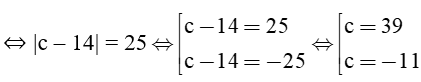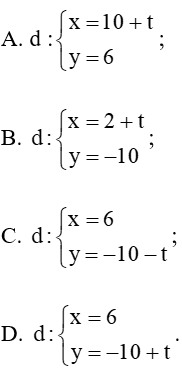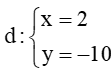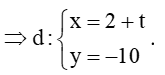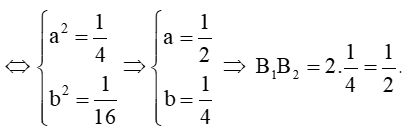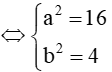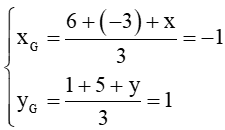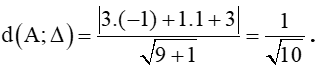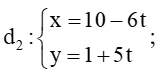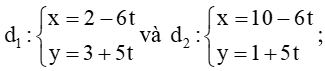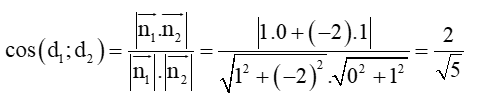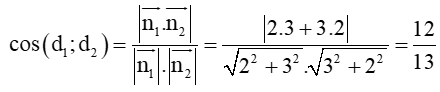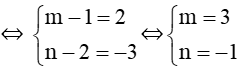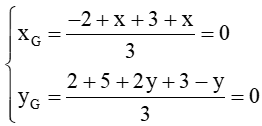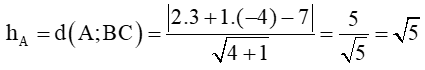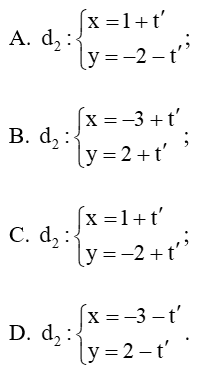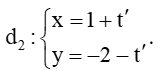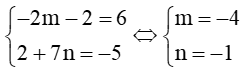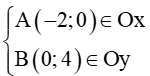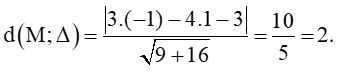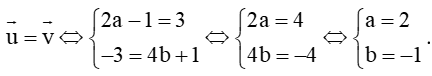50 câu Trắc nghiệm Ôn tập Chương 7 (có đáp án 2024) – Toán 10 Cánh diều
Bộ 50 câu hỏi trắc nghiệm Toán 10 (có đáp án) Ôn tập Chương 7: Phương pháp tọa độ trong mặt phẳng đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 10 Chương 7.
Trắc nghiệm Toán 10 Ôn tập Chương 7
Câu 1. Đường tròn (C) đi qua ba điểm A (– 1; – 2), B(0; 1) và C(1; 2) có phương trình là:
A. (x – 4)2 + (y – 2)2 = 52;
B. (x – 4)2 + (y + 2)2 = 52;
C. (x + 4)2 + (y + 2)2 = 52;
D. (x + 4)2 + (y – 2)2 = 52.
Đáp án đúng là: B
Gọi phương trình đường tròn cần tím có dạng (C): x2 + y2 + 2ax + 2by + c = 0.
Vì (C) đi qua các điểm A, B, C nên lần lượt thay tọa độ các điểm vào phương trình (C) ta được hệ phương trình:
Vậy phương trình đường tròn (C) là x2 + y2 – 8x + 4y – 5 = 0 ⇔ (x – 4)2 + (y + 2)2 = 52.
Câu 2. Viết phương trình tiếp tuyến của đường tròn (C):x2+y2+4x+4y−17=0,
biết tiếp tuyến vuông góc đường thẳng d: 3x – 4y – 2018 = 0.
A. 3x – 4y + 39 = 0 hoặc 3x – 4y – 11 = 0;
B. 4x + 3y + 39 = 0 hoặc 3x – 4y – 11 = 0;
C. 3x – 4y + 39 = 0 hoặc 4x + 3y – 11 = 0;
D. 4x + 3y + 39 = 0 hoặc 4x + 3y – 11 = 0.
Đáp án đúng là: D
Xét phương trình đường thẳng d có VTPT là →ud=(3; – 4) suy ra VTCP của đường thẳng d là →ud=(4; 3).
Vì phương trình tiếp tuyến vuông góc với đường thẳng d nên nhận →ud=(4; 3) làm VTPT khi đó phương trình tiếp tuyến có dạng: 4x + 3y + c = 0
Ta có: Đường tròn (C) có tâm I(– 2; – 2), R = 5
Bán kính đường tròn:
Suy ra có hai phương trình tiếp tuyến thỏa mãn: 4x + 3y + 39 = 0 hoặc ∆:4x + 3y –11 = 0.
Câu 3. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua gốc tọa độ O(0; 0) và điểm M(a; b)?
A. (– a; – b);
B. (a; b);
C. (1; a);
D.(1; b).
Đáp án đúng là: B
Ta có:
đường thẳng OM có VTCP:
Câu 4. Một đường thẳng có bao nhiêu vectơ chỉ phương?
A. 2;
B. 5;
C. 7;
D. Vô số.
Đáp án đúng là: D
Một đường thẳng có vô số vectơ chỉ phương
Câu 5. Viết phương trình tham số của đường thẳng d đi qua điểm M(6; –10)và vuông góc với trục Oy?
Đáp ứng đúng là: B
Ta có: , mặt khác
Phương trình tham số 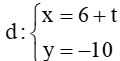
hay A (2; – 10) d
Câu 6. Xét vị trí tương đối của hai đường thẳng:
: 3x – 2y – 3 = 0 và : 6x – 2y – 8 = 0
A. Trùng nhau;
B. Song song;
C. Vuông góc với nhau;
D. Cắt nhau nhưng không vuông góc nhau.
Đáp án đúng là: D
Ta có: : 3x – 2y – 3 = 0 có VTPT là = (3; – 2) và : 6x – 2y – 8 = 0 có VTPT là = (6; – 2).
Ta có: nên hai vectơ và không cùng phương.
Do đó đường thẳng d1 và d2 cắt nhau.
Ta lại có nên d1 và d2 không vuông góc với nhau.
Vậy hai đường thẳng cắt nhau nhưng không vuông góc.
Câu 7. Elip có độ dài trục bé bằng:
A. 2;
B. 4;
C. 1;
D.
Đáp án đúng là: D
Phương trình của Elip là có độ dài trục lớn B1B2 = 2b.
Xét
Câu 8. Đường thẳng nào là đường chuẩn của parabol
A.
B.
C.
D. .
Đáp án đúng là: D
Phương trình chính tắc của parabol
2p = 2 p =1. Phương trình đường chuẩn là =.
Câu 9. Elip có tiêu cự bằng:
A.
B. 5,
C. 10,
D. 2.
Đáp án đúng là: D
Gọi phương trình của Elip là có tiêu cự là 2c
Xét
= 16 – 4 = 12c = 2c = 2.
Câu 10. Trong hệ tọa độ Oxy cho tam giác ABC có A (6 ; 1), B (–3 ; 5) và trọng tâm G (–1 ;1). Tìm tọa độ đỉnh C?
A. C (6 ; – 3) ;
B. C (– 6 ; 3) ;
C. C (– 6 ; – 3) ;
D. C (– 3 ; 6).
Đáp án đúng là : C
Gọi toạ độ C(x ; y), ta có:
Vì G là trọng tâm tam giác ABC nên :
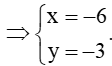
Câu 11. Phương trình tiếp tuyến d của đường tròn (C): x2 + y2 – 3x – y = 0 tại điểm N(1; – 1) là:
A. d: x + 3y – 2 = 0;
B. d: x – 3y + 4 = 0;
C. d: x – 3y – 4 = 0;
D. d: x + 3y + 2 = 0.
Đáp án đúng là: D
Xét phương trình (C): x2 + y2 – 3x – y = 0 ⇔ .
Khi đó đường tròn (C) có tâm nên tiếp tuyến tại N có VTPT là:
Nên có phương trình là: 1(x – 1) +3(y + 1) = 0x + 3y + 2 = 0.
Câu 12. Khoảng cách từ giao điểm của đường thẳng x – 3y + 4 = 0 và 2x + 3y – 1 = 0 đến đường thẳng : 3x + y + 3 = 0 bằng:
A. ;
B.;
C. ;
D. 2.
Đáp án đúng là: C
+) Giao điểm của hai đường thẳng:
Ta có: 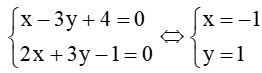
+) Khoảng cách từ A đến : 3x + y + 3 = 0:
Câu 13.Góc tạo bởi hai đường thẳng nào dưới đây bằng 90°
A. : 6x – 5y + 4 = 0 và
B.
C. d1: x – 2y + 4 = 0 và d2: y + 1 = 0;
D. 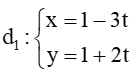
Đáp án đúng là: A
+) Đường thẳng : 6x – 5y + 4 = 0 có VTPT là
Đường thẳng 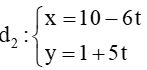
Ta có: . Do đó d1 ⊥ d2 hay góc giữa hai đường thẳng bằng 90°.
+) Đường thẳng 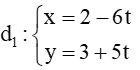
Đường thẳng 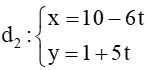
Ta có: nên và cùng phương. Do đó hai đường thẳng d1 song song hoặc trùng d2. Do đó góc giữa hai đường thẳng bằng 0°.
+) Đường thẳng d1: x – 2y + 4 = 0 có VTPT là
Đường thẳng d2: y + 1 = 0 có VTPT là
Áp dụng công thức tính góc giữa hai đường thẳng ta được:
⇒ (d1 ; d2) ≈ 26°34’.
+) Đường thẳng 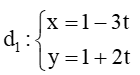
Đường thẳng d2: 3x + 2y – 4 = 0 có VTPT là
Áp dụng công thức tính góc giữa hai đường thẳng ta được:
⇒ (d1 ; d2) ≈ 22°37’.
Câu 14. Trong hệ tọa độ Oxy cho ba điểm A(3; 5), B(1; 2), C(5; 2) và D(m ; n) . Tính m + n để ACDB là hình bình hành.
A. m + n = 3;
B. m + n = – 1;
C. m + n = 2;
D. m + n = 4.
Đáp án đúng là: C
Ta có: ; .
Để ACDB là hình bình hành thì =
⇒ m + n = 3 + (– 1) = 2.
Câu 15. Trong hệ tọa độ Oxy cho tam giác ABC có A (– 2 + x ; 2), B (3 ; 5 + 2y), C(x ; 3 – y). Tìm tổng 2x + y với x, y để O (0 ; 0) là trọng tâm tam giác ABC?
A. – 7;
B. – 2 ;
C. – 11;
D. .
Đáp án đúng là : C
Vì O là trọng tâm tam giác ABC nên, ta có :
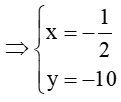
Câu 16. Trong hệ tọa độ Oxy cho ba điểm A (1; 3) ; B (– 1; 2) ; C (– 2 ; 1) . Tìm tọa độ của vectơ .
A. (– 5; – 3);
B. (1; 1);
C. (– 1; 2);
D. (– 1; 1).
Đáp án đúng là : B
Ta có 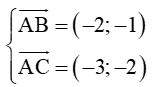
Câu 17. Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua hai điểm A(a; 0) và B(0; b)?
A. (a; – b);
B. (a; b);
C. (– b; a);
D. (b; a).
Đáp án đúng là: A
Ta có:
đường thẳng AB có VTCP hoặc
đường thẳng AB có VTPT là .
Câu 18. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(3; -4);B(1; 5) và C(3; 1). Tính diện tích tam giác ABC.
A. 10;
B. 5;
C.
D.
Đáp án đúng là: B
+) Viết phương trình đường thẳng BC; độ dài BC
- Ta có: B(1; 5); C(3; 1) ⇒ (2; – 4) là vectơ chỉ phương của đường thẳng BC
Ta chọn = (2; 1) là vectơ pháp tuyến của đường thẳng BC (), ta viết được phương trình đường thẳng qua BC như sau: 2.(x – 1) + 1.(y – 5) = 0 hay
2x + y – 7 = 0
- Độ dài BC: BC =
+) Tính độ dài đường cao kẻ từ A:
Độ dài đường cao kẻ từ A chính là khoảng cách từ A đến phương trình đường thẳng qua BC, ta có:
+) Diện tích tam giác ABC:
= = 5.
Câu 19. Tọa độ tâm I và bán kính R của đường tròn (C): x2 + y2 = 16 là:
A. I (0; 0), R = 9;
B. I (0; 0), R = 81;
C. I (1; 1), R = 3;
D. I (0; 0), R = 4;
Đáp án đúng là: D
Ta có:(C): x2 + y2 = 16
I (0; 0); R = = 4.
Câu 20.Cho đường thẳng 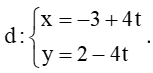
Đáp án đúng là: A
Đường thẳng 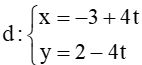
Với t = 1 thì 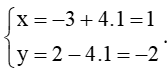
Vì vậy đường thẳng d trùng với đường thẳng
Câu 21. Cho = (–2m; 2), = (2; –7n). Tìm giá trị của m và n để tọa độ của vectơ = (6; –5).
A. m = 4 và n = – 1;
B. m = – 4 và n = – 1;
C. m = 4 và n = 1;
D. m = – 4 và n = 1.
Đáp án đúng là : B
Ta có : = (–2m; 2) – (2; –7n) = (–2m –2; 2 + 7n)
Mà = (6; – 5)
Nên ta có:
Vậy m = – 4 và n = – 1.
Câu 22. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A(– 3; 2) và B(1; 4).
A. (1; 3);
B. (2; 1);
C. (1; 3);
D. (3; 1).
Đáp án đúng là: B
Đường thẳng đi qua hai điểm A(– 3; 2) và B(1; 4) có VTCP là:
= (4; 2) = 2(2; 1)hay .
Câu 23. Cho A (2; –4), B (–5; 3). Tìm tọa độ của .
A. (7; –7);
B. (–7; 7);
C. (9; –5);
D. (1; –5).
Đáp án đúng là: B
Ta có : = (–5 – 2; 3 – (–4)) = (–7; 7).
Câu 24. Trong hệ tọa độ Oxy cho tam giác ABC có B (9 ; 7), C (11 ; –1). Gọi M, N lần lượt là trung điểm của AB, AC. Tìm tọa độ vectơ ?
A. (2 ; – 8) ;
B. (1 ; – 4) ;
C. (10 ; 6) ;
D. (5 ; 3).
Đáp án đúng là : B
Xét tam giác ABC, có :
M là trung điểm AB
N là trung điểm AC
Suy ra MN là đường trung bình tam giác ABC
Theo tính chất đường trung bình,ta có :
= .(2; –8) = (1; –4).
Câu 25. Trong hệ tọa độ Oxy cho ba điểm A (–1 ; 1), B (1 ; 3), C (–1; 4) , D(1; 0). Khẳng định nào sau đây đúng?
A.
B.
C.
D.
Đáp án đúng là: C
Ta có : 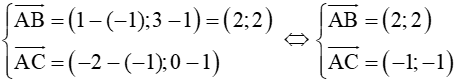
= -2. (-1; -1) = .
Câu 26. Phương trình đường thẳng cắt hai trục tọa độ tại A(– 2 ; 0) và B(0 ; 4) là:
A. 2x – 3y + 2 = 0;
B. 4x – 2y + 8 = 0;
C. 3x – 3y – 6 = 0;
D. 2x – 3y – 5 = 0.
Đáp án đúng là : B
Ta có:
Phương trình đường thẳng:4x – 2y + 8 = 0
Câu 27. Khoảng cách từ điểm M( –1; 1) đến đường thẳng : 3x – 4y – 3 = 0 bằng:
A.
B. 2;
C.
D.
Đáp án đúng là: B
Áp dụng công thức tính khoảng cách từ một điểm đến đường thẳng ta có:
Câu 28. Cho hai vectơ và . Tìm các số thực a và b sao cho cặp vectơ đã cho bằng nhau:
A. a = 2, b = – 1;
B. a = – 1, b = 2;
C. a = – 1, b = – 2;
D. a = 2, b = 1.
Đáp án đúng là: A
Để
Vậy a = 2 và b = – 1.
Câu 29. Trong hệ tọa độ Oxy cho = (5 ; 2), = (10 ; 8). Tìm tọa độ của vectơ .
A. (15; – 10);
B. (2; 4);
C. (– 5; – 10);
D. (50; 16).
Đáp án đúng là: C
Ta có: 3= 3(5 ; 2) = (15 ; 6) ; 2 = 2(10 ; 8) = (20 ; 16)
= (15 – 20 ; 6 – 16) = (– 5; – 10).
Câu 30. Đường tròn (C): x2 + y2 – 8x + 2y + 6 = 0 có tâm I, bán kính R lần lượt là:
A. I (3; – 1), R = 4;
B. I (– 3; 1), R = 4;
C. I (4; – 1), R = ;
D. I (– 3; 1), R = 2.
Đáp án đúng là: C
Ta có:(C): x2 + y2 – 8x + 2y + 6 = 0⇔ x2 + y2 – 2.4x – 2.(– 1)y + 6 = 0
⇒a = 4; b = – 1 và c = 6
⇒I (4; – 1), .